归并排序的递归过程如下，该递归树的高度为log2n（计算过程：假设待排序的数组元素个数为n，设高度为x，x意味着n个元素需要连续二分x次才剩下1个元素，即n/2^x=1，x=log2n），每一层的总比较次数为n，所以时间复杂度为nlogn。
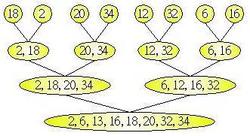
快速排序的分析过程类似。快速排序的平均时间复杂度同样为nlogn。假设在平均情况下每次选取的基准值均为该数组的中间值，因此每次都将数组分成两半，直到分割到只剩一个元素。假设n个元素平分了x次后只剩1个元素，则n/2^x=1，x=log2n。每次分割后的比较次数为n（参考上图），所以时间复杂度为nlogn。
