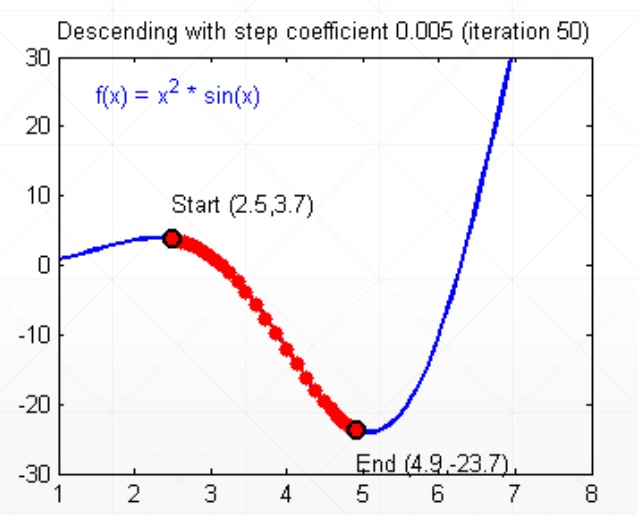
1.什么是梯度
各个方向的偏微分组成的向量
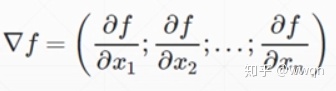
举例说明,z对x的偏微分和对y的偏微分如下,则梯度是(-2x,2y)的这样一个向量
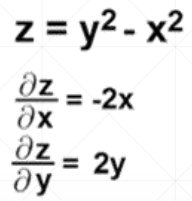
在光滑连续函数的每个点上,都可以计算一个梯度,也就是一个向量,用小箭头表示,那么梯度越大的地方,向量的模值就会越大,箭头就会越长,如图所示
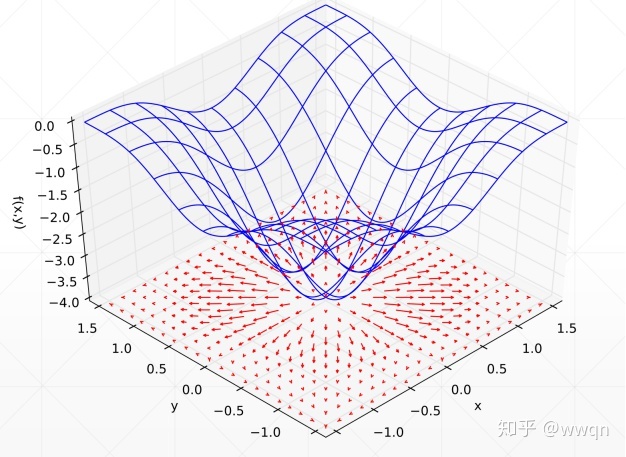
可以看到,越平坦的地方,箭头越短,说明梯度越小,所以梯度反映了图像的变化趋势
2.通过梯度更新参数,让目标函数(损失函数)趋于极小值
更新参数的目的是让目标函数找到一个极小值,这个目标函数就是我们说的损失函数
在函数中的每个变量称为参数,对图二中的例子进一步分析,x,y两个就是参数,如图,x沿着x正方向,所以△x>0,如果函数是上升的,是在上坡的,则△z>0,这时候参数x应该往回走,即应该减小。如果函数是下降,是下坡的,则△z<0,这时候参数x应该往前走,即应该增大,所以参数和梯度的关系应该是相反的
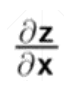
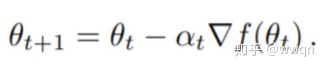
左边是更新后的参数,αt是学习率,防止每次改变的幅度过大,一不小心跳过了最小值点
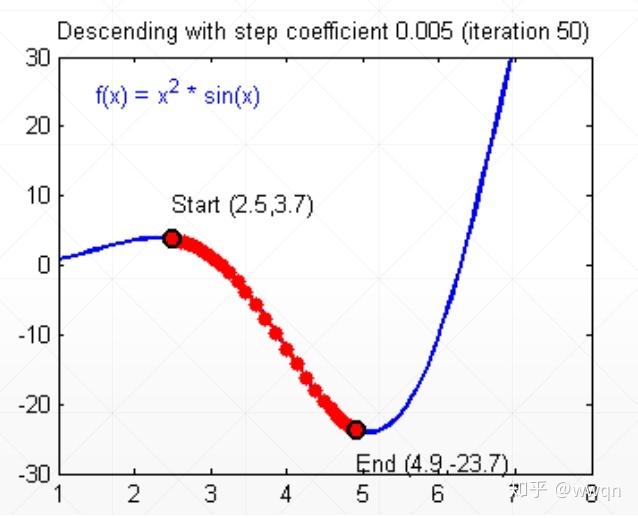
3.通过tensorflow计算梯度
损失函数定义在
with tf.GradientTape() as tape:tape.watch([w])loss = w*x#在这里定义损失函数计算梯度在
grade = tape.gradient(loss,w)#在这里计算梯度完整代码
import tensorflow as tf
w = tf.constant(1)
x = tf.constant(2.)
with tf.GradientTape() as tape:tape.watch([w])loss = w*x#在这里定义损失函数
grade = tape.gradient(loss,w)#在这里计算梯度
with tf.Session() as sess:print(sess.run(grade))








...)









