leetcode 5 最长回文子串
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"思路:
动态规划
为了改进暴力法,我们首先观察如何避免在验证回文时进行不必要的重复计算。考虑
我们给出
因此,
基本示例如下:
这产生了一个直观的动态规划解法,我们首先初始化一字母和二字母的回文,然后找到所有三字母回文,并依此类推…
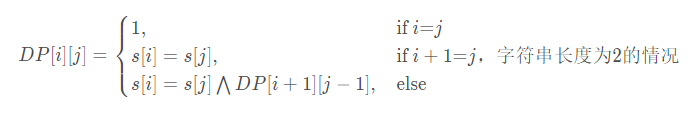
复杂度分析
- 时间复杂度:O(n^2)O(n2),这里给出我们的运行时间复杂度为 O(n^2)O(n2) 。
- 空间复杂度:O(n^2)O(n2),该方法使用 O(n^2)O(n2) 的空间来存储表。
具体写码的时候用一个变量(代码中的sub)来记录目前最长的子串长度,用一个list(代码中的max_len)来记录最长子串的坐标
另一个leetcode上速度比较快的算法有点类似滑动窗口法,维护一个最大长度为lenth的窗口,并使用python语法糖q == q[::-1]来判断是否是回文字符串,但是要注意的是维护窗口时要同时维护奇数和偶数两种窗口。
答案:
class Solution(object):def longestPalindrome(self, s):""":type s: str:rtype: str"""n = len(s)if n == 0:return ''if n == 1:return sres = [[0 for _ in range(n)] for _ in range(n)]sub = 1max_len = [0,0]for i in range(n):res[i][i] = 1if i != n-1 and s[i] == s[i+1]:res[i][i+1] = 1sub = 2max_len=[i,i+1]for i in range(n):for j in range(1,min(i,n-i)+1):if i-j>=0 and i+j<n and res[i-j+1][i+j-1] and s[i-j]==s[i+j]:res[i-j][i+j] =1#print 1+2*jif sub<1+2*j:sub = 1+2*jmax_len = [i-j,i+j]#print sub,max_lenif i-j>=0 and i+1+j<n and res[i-j+1][i+j] and s[i-j] == s[i+j+1]:res[i-j][i+j+1] =1if sub<2+2*j:sub = 1+2*jmax_len = [i-j,i+j+1]#print sub,max_lenreturn s[max_len[0]:(max_len[1]+1)]class Solution(object):def longestPalindrome(self, s):""":type s: str:rtype: str"""if len(s) == 1 or s == s[::-1]:return sstart = 0length = 1for i in range(len(s)):p = s[i-length-1:i+1]q = s[i-length:i+1]if i-length-1 >= 0 and p == p[::-1]:start = i-length-1length += 2if i-length >=0 and q == q[::-1]:start = i - lengthlength += 1return s[start:start+length][647] 回文子串
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被计为是不同的子串。
示例 1:
输入: "abc"
输出: 3
解释: 三个回文子串: "a", "b", "c".
示例 2:
输入: "aaa"
输出: 6
说明: 6个回文子串: "a", "a", "a", "aa", "aa", "aaa".
注意:
输入的字符串长度不会超过1000。
思路:
这道题的动态规划思路跟上一道题(第五题)完全一样,只不过在具体代码的时候,使用一个变量来记录回文子串的个数。
[516] 最长回文子序列
给定一个字符串s,找到其中最长的回文子序列。可以假设s的最大长度为1000。
示例 1:
输入:
"bbbab"
输出:
4
一个可能的最长回文子序列为 "bbbb"。
示例 2:
输入:
"cbbd"
输出:
2
一个可能的最长回文子序列为 "bb"。
思路:
这道题跟上两道题的动态规划思路完全不一样,首先,这道题寻找的是最长回文子序列,子序列可以不相连。其次,这道题要返回的是最长回文子序列的长度,不关心子序列,所以构造动态规划数组时也稍有不同。具体来说:
引入
递推公式可以表示为:
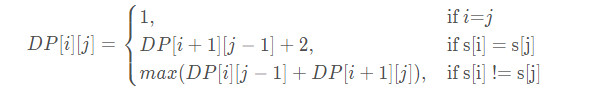
注意在具体代码的时候,循环应该是先判断间隔距离为1的所有字符对,然后依次增加。
答案:
class Solution(object):def longestPalindromeSubseq(self, s):""":type s: str:rtype: int"""n = len(s)if n<=1:return nif n==2:if s[0]==s[1]:return 2else:return 1resgrid = [[0 for _ in range(n)] for _ in range(n)]for i in range(n):resgrid[i][i]=1for gap in range(1,n):for i in range(n):if i+gap>=n:breakl = ih = i+gapif s[l]==s[h]:resgrid[l][h] = resgrid[l+1][h-1]+2else:resgrid[l][h]=max(resgrid[l+1][h],resgrid[l][h-1])return resgrid[0][n-1]