迭代剔除策略:先站在所有人的角度,删除所有的劣势策略,然后重复这个过程。
Game One--中间选民定理的例子
博弈者:2个Players需要选择自己的政治立场。
策略选项:一共有1-10种政治立场,每种都有10%的选民支持。
收益:候选者要最大化取得选票,他们需要胜利。
1代表极端左派(保守),10代表极端右派(激进)
这些选民最终会选择最接近他们的候选人进行投票。
这个博弈不会出现平局。
分析:
这里存在一个劣势策略,那就是选择立场1。
选择了立场1,收益没有其他立场收益高。
比如:
V1 \(u_i\)(1,1) = 50%,\(u_i\)(2,1) = 90%
V2 \(u_i\)(1,2) = 10%,\(u_i\)(2,2) = 50%
V3 \(u_i\)(1,3) = 15%,\(u_i\)(2,3) = 20%
V4 \(u_i\)(1,4) = 20%,\(u_i\)(2,4) = 25%
…………
同理可以得到另一个劣势策略,那就是选择立场10
结论:此时立场2严格优于1,立场9严格优于10
以此类推,迭代删除最终会得到的优势策略为立场5和立场6.
这个模型在政治学中叫做"中间选民定理"
预测了候选人将会向中间立场靠拢。
缺陷:
1.现实中有多名候选人,不只是两名
2.候选人的立场可能不坚定,不能承诺政策实施
3选择候选人的时侯是包含其他维度(条件)的,比如选民喜好等
4.选民的投票不是均匀分布的(但是实际不影响结果)
5.选民可能会弃权
Conclusion:
模型都是抽象的对于上面的例子是否立场3严格优于立场2?
由于U1(2,1)=90% < U1(3,1)=85%
所以立场3不严格优于立场2
但是当我们已经明确候选人已经不会选择立场1和立场10这两个严格劣势策略的时候,
立场3才严格优于立场2。
这里只是相当与去掉了立场1和立场10,但是选票和选民依然存在。
V2 \(u_i\)(2,2) = 50%, \(u_i\)(3,2) = 80%
V3 \(u_i\)(2,3) = 20%, \(u_i\)(3,3) = 50%
V4 \(u_i\)(2,4) = 25%, \(u_i\)(3,4) = 30%
V5 \(u_i\)(2,5) = 30%, \(u_i\)(3,5) = 35%
V6 \(u_i\)(2,6) = 35% ,\(u_i\)(3,6) = 40%
V7 \(u_i\)(2,7) = 40% ,\(u_i\)(3,7) = 45%
V8 \(u_i\)(2,8) = 45%, \(u_i\)(3,8) = 50%
V9 \(u_i\)(2,9) = 50% ,\(u_i\)(3,9) = 55%
…………A different approach :Best Response
Game Two--Player1会选择上中下,Player2可以选择左右,
收益如下:
| P1/P2 | L | R |
|---|---|---|
| U | 5,1 | 0,2 |
| M | 1,3 | 4,1 |
| D | 4,2 | 2,3 |
如果是Player1,他的BR(Best Response)?
选择"上"是对应Player2选择"左"的最佳选择
选择"中"是对应Player2选择"右"的最佳选择
当对手选择左右的概率相等的时候,此时最好的选择是下。
Ui(u)=0.55+50=2.5收益
Ui(M)=10.5+40.5=2.5收益
Ui(D)=0.54+0.52=3收益
但是情况可能不一样,比如Player2选择左右的概率为pos1,pos2时就需要重新计算。
假设Player2选择右的概率为\(P_x\),收益如下:
\(u(U,L)\) = \((1-P_x)\)* 5 + 0 * \(P_x\)= 5\(P_x\)
\(u(D,L)\) = \((1-P_x)\) 1 + 4 * \(P_x\) = 4 - 3 * \(P_x\)
\(u(M,L)\) = \((1-P_x)\)* 4 + 2 * \(P_x\) = 2 + 2 * \(P_x\)
所以画图表示如下:
其中\(P_1\)=\(u(U,L)\),\(P_2\)=\(u(D,L)\) ,\(P_3\)=\(u(M,L)\),横坐标表示Player2选择左的概率。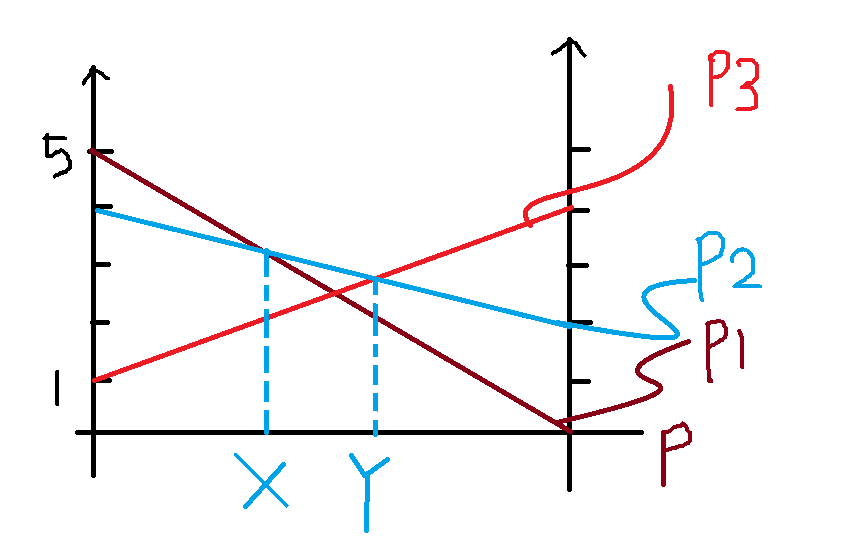
如果认为对方选择右(R)的概率小于x的话,BR=U,相对的,如果概率大于y时,
BR=M,如果概率落在\(x\)~\(y\)之间,则BR=D。
联立三个直线方程,可以求得
\(x=1/3\),\(y=2/3\)



--类的创建)






)








