给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

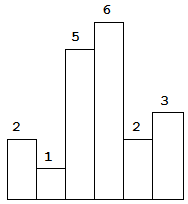
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

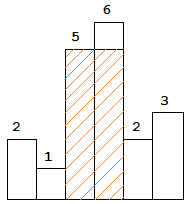
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

 

示例:

输入: [2,1,5,6,2,3]
输出: 10

思路：

时间复杂度：o(n^2)

从i=0开始遍历，每次都计算出以当年位置为最后位置的各矩形面积并比较大小

例如本题，i=3时，dp[3]=6

只包含当前柱体的面积是6

向前遍历，宽度加1，高度取二者中最小的   即2*5=10

继续向前遍历，宽度加1，高度取三者中最小，即3*1=3

继续........即4*1=4

提交的代码：

class Solution {
    public int largestRectangleArea(int[] heights) {
       if(heights.length==0)
    {
        return 0;
    }
    int max=heights[0],x,y,t;
    for(int i =0;i<heights.length;i++)
    {
        x=0;
        y=heights[i];
        for(int j=i;j>=0;j--)
        {
            x++;
            y = Math.min(y, heights[j]);
            t = x*y;
            max = Math.max(max, t);
        }
    }
    return max;
    }
}

完整的代码：

public class Solution84 {
public static int largestRectangleArea(int[] heights) {
    if(heights.length==0)
    {
        return 0;
    }
    int max=heights[0],x,y,t;
    for(int i =0;i<heights.length;i++)
    {
        x=0;
        y=heights[i];
        for(int j=i;j>=0;j--)
        {
            x++;
            y = Math.min(y, heights[j]);
            t = x*y;
            max = Math.max(max, t);
        }
    }
    return max;
        
    }
public static void main(String[] args)
{
    int nums[] = {2,1,5,6,2,3};
    System.out.println(largestRectangleArea(nums));
}
}