决策树表示对象属性（比如贷款用户的年龄、是否有工作、是否有房产、信用评分等）和对象类别（是否批准其贷款申请）之间的一种映射。使用层层推理来实现最终的分类。

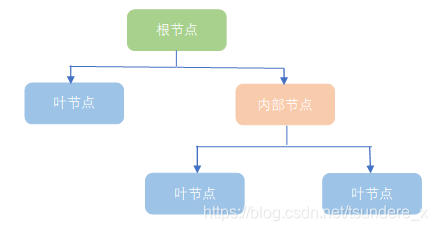
 根节点：包含样本的全集
 内部节点：对应特征属性测试
 叶节点：代表决策的结果

预测时，在树的内部节点处用某一属性值进行判断，根据判断结果决定进入哪个分支节点，直到到达叶节点处，得到分类结果。

这是一种基于 if-then-else 规则的有监督学习算法，决策树的这些规则通过训练得到，而不是人工制定的。

决策树是最简单的机器学习算法，它易于实现，可解释性强，完全符合人类的直观思维，有着广泛的应用。

决策树学习的三个步骤

一、特征选择

特征选择决定了使用哪些特征来做判断。在训练数据集中，每个样本的属性可能有很多个，不同属性的作用有大有小。因而特征选择的作用就是筛选出跟分类结果相关性较高的特征，也就是分类能力较强的特征。

在特征选择中通常使用的准则是：信息增益

二、决策树生成
选择好特征后，就从根节点出发，对节点计算所有特征的信息增益，选择信息增益最大的特征作为节点特征，根据该特征的不同取值建立子节点；对每个子节点使用相同的方式生成新的子节点，直到信息增益很小或者没有特征可以选择为止。

三、决策树剪枝
剪枝的主要目的是对抗过拟合（模型的泛化能力差），通过主动去掉部分分支来降低过拟合的风险。

三种典型的决策树算法：ID3、C4.5、CART

ID3：最早提出的决策树算法，利用信息增益来选择特征
C4.5：ID3的改进版，不是直接使用信息增益，而是引入“信息增益比”指标作为特征的选择依据
CART：可用于分类，也可用于回归问题。使用基尼系数取代了信息熵模型。

关于信息增益（Information Gain）：

信息熵表示的是不确定性。非均匀分布时，不确定性最大，此时熵就最大。当选择某个特征，对数据集进行分类时，分类后的数据集的信息熵会比分类之前小，其差值表示为信息增益。信息增益可以衡量某个特征对分类结果的影响大小。

对于一个数据集，特征A作用之前的信息熵计算公式为：

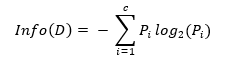
式中，D为训练数据集；c 为类别数量；P_i 为类别 i 样本数量占所有样本的比例。对应数据集 D，选择特征 A 作为决策树判断节点时，在特征 A 作用后的信息熵为 InfoA (D) （特征 A 作用后的信息熵计算公式），计算如下：

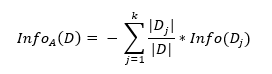
式中，k 为样本 D 被分为 k 个子集。