在二维平面上，把两类数据分开需要一条直线。到了3微空间，要把两类数据分开，就需要一个平面。把上述分类机制扩展到基本情形，在高维空间里，把两类数据分开，则需要一个超平面。直线和平面是超平面在2维和3维空间的表现形式。当我们处理的是100维数据时，超平面就是一个99维的对象。

支持向量：
我们寻找分类函数 y=f(x)= ω^T x+b，超平面上的点代入这个分类函数，得到 f(x)=0，超平面一边的数据点代入分类函数，得到 f(x)= 1；在超平面另一边的数据点代入分类函数得到 f(x)= -1。在二维平面上，这个分类函数对应一根直线 y=f(x)=ax+b。

在二维平面上确定一根直线，就是确定上述方程中的 a 和 b。在高维空间上确定一个超平面，则需要确定 ω 向量和 b 向量。我们需要寻找一个超平面，它到两个类别数据点的距离都尽可能大，这样的超平面为最优的超平面。

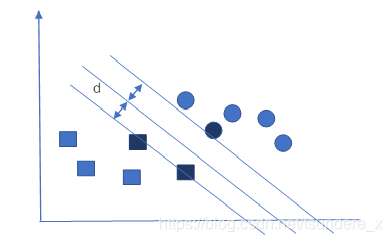
在上图中，中间的那根直线到两类数据点的距离是相等的，为了确定这根直线，不需要所有的数据点（向量），只需要图中显示为深色的数据点（向量），这些向量唯一确定了数据划分的直线（超平面），称为支持向量（Support Vector）。

支持向量机是一个对高维数据进行分类的分类器。数据点被划分到两个不相交的半空间（Half Space），从而实现分类，划分两个半空间的是一个超平面，SVM 分类的主要任务是寻找到和两类数据点都具有最大距离的超平面，目的是使得把两类数据点分开的划分范围最大化。