
来源:AI科技评论
作者:杏花、莓酊
编辑:琰琰
数论是人类知识最古老的一个分支,然而它最深奥的秘密与其最平凡的真理是密切相连的。数学原理极易从事实中归纳出来,但证明却隐藏的极深。可以说数学,是一切科学的基础。就如诺贝尔奖得主费曼说:如果没有数学语言,宇宙似乎是不可以描述的。
徐宗本院士曾表示,数学与 AI 的关系是「融通共进」。一方面,人工智能的基础之一是数学,因此人工智能想要行稳致远,就必须先把数学的基本问题解决好;另一方面,人工智能的发展也对数学领域的研究产生了重要的推动作用。
只是目前为止,人工智能技术未能在纯数学研究中取得重大突破。
12月1日,Nature杂志刊登文章《Advancing mathematics by guiding human intuition with AI》,验证了机器学习在发现数学猜想和定理方面有着巨大潜力。

相关链接:
https://www.nature.com/articles/s41586-021-04086-x
这篇文章出自人工智能明星公司DeepMind团队,他们与数学领域的顶级科学家合作,在拓扑学和表象理论方面证明了两个新猜想:
与悉尼大学Geordie Williamson教授合作接近证明了一个关于卡兹丹—卢斯提格多项式的古老猜想,这个猜想已困扰数学家们40多年。
与牛津大学Marc Lackenby教授和András Juhász教授一起,通过研究拓扑学纽结理论观察到代数和几何不变量之间的惊人联系。这是利用机器学习做出的第一个重大数学发现。
1
DeepMind开启数学新范式
在这篇最新论文中,计算机科学家和数学家们首次使用AI来帮助证明或提出新的数学定理,包括复杂理论中的纽结理论和表象理论。

该论文的研究团队提出采用一种机器学习模型,来发现数学对象之间的潜在模式和关联,用归因技术加以辅助理解,并利用这些观察进一步指导直觉思维和提出猜想的过程。
这次研究中,AI帮助探索的数学方向是表象理论。表象理论属于线性对称理论,是利用线性代数探索高维空间的数学分支,而该论文的合著者Williamson教授是全球公认的表象理论的领导者。
Williamson教授说:“在我所研究的领域中,为了证明或反驳长期存在的猜想,有时需要考虑跨越多维度的无限空间和极其复杂的方程组”。虽然计算机长期以来一直被用来为实验数学生成数据,但识别有趣模式的任务主要依赖于数学家自己的直觉。
众所周知,数学家的直觉在数学发现中起着极其重要的作用——“只有结合严格的形式主义和良好的直觉思维,才能解决复杂的数学问题”。
然而,DeepMind的新突破打开了一扇崭新的大门。
DeepMind团队在论文中描述了一种通用的框架方法,在这个框架之下,数学家可以使用ML工具来指导他们对复杂数学对象的直觉,验证关系存在的假设,并理解这些关系。
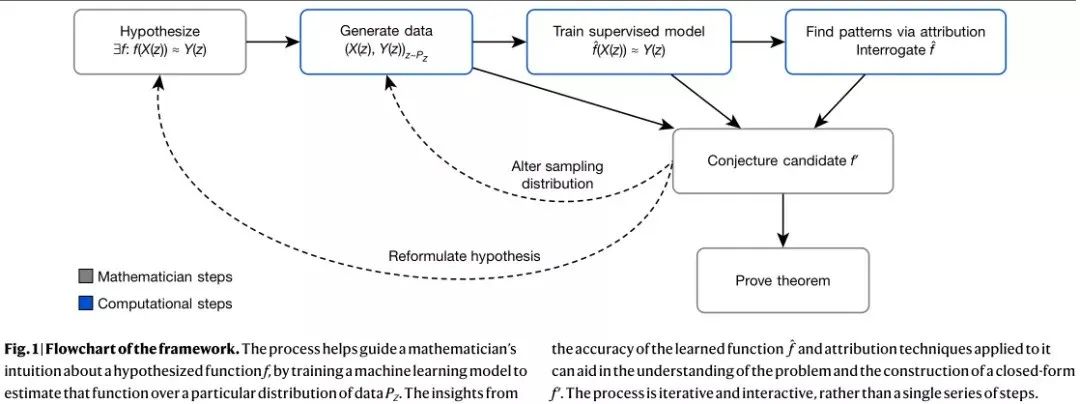
Williamson教授就利用AI,在证明关于Kazhdan-Lusztig多项式的古老猜想的道路上离目标越来越近,当然,这些猜想涉及高维代数中的深度对称性。可以说,Kazhdan-Lusztig(KL)是代数群表示论近40年来最重要的发展之一。
而来自牛津大学的Marc Lackeby教授和András Juhász教授,则进一步研究了该过程。
他们发现了纽结的代数和几何不变量之间惊人的关联,建立了数学中一个全新的定理。这些不变量有许多不同的推导方式,研究团队将目标主要聚焦在两大类:双曲不变量和代数不变量。两者来自完全不同的学科,这增加了研究的挑战性和趣味性。
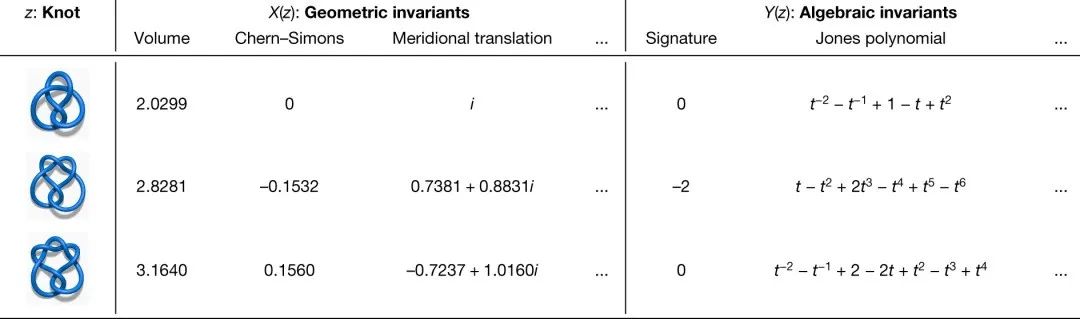
研究团队假设,在一个纽结的双曲不变量和代数不变量之间存在着一种未被发现的关系。监督学习模型能够检测到大量几何不变量和签名之间存在的模式。如下图所示,由归因技术确定最相关的特征。
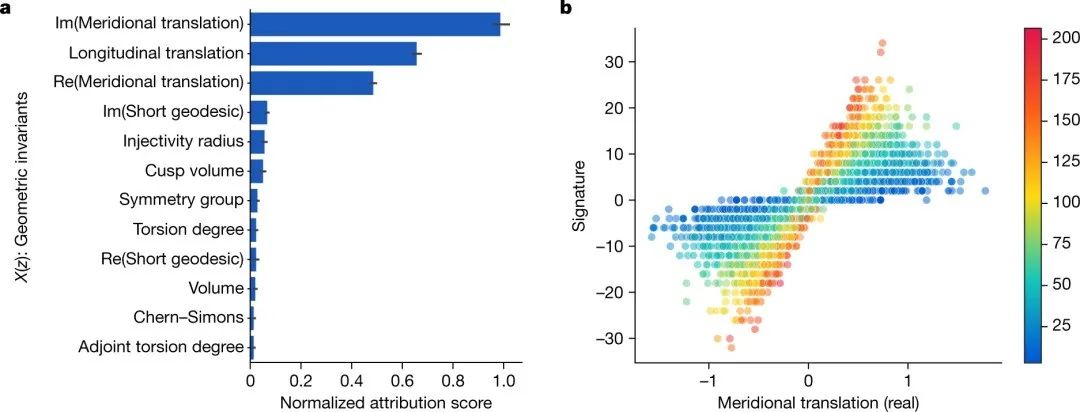
通过计算归因技术确定的最相关的显著子图,分析这些图与原始图相比的边缘分布,有助于进一步探索结构证据。
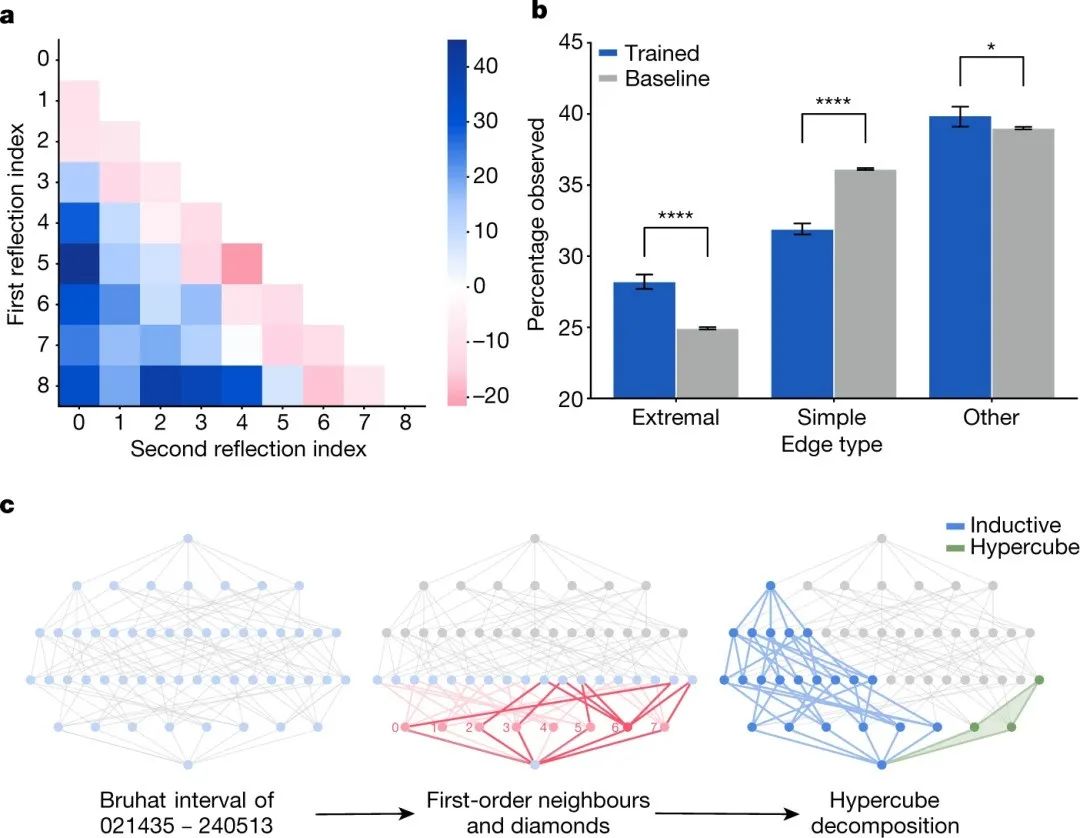
图注:a. 在预测 q4 时,与数据集中跨区间的平均值相比,显着子图中存在的反射百分比增加的示例热图。b. 与来自数据集的10个相同大小的自举样本相比,模型的10次再训练在显着子图中观察到的每种类型的边缘的百分比。误差线是95%的置信区间,显示的显着性水平是使用双侧双样本t检验确定的。* p < 0.05;****p < 0.0001。c. 通过假设、监督学习和归因的迭代过程发现的有趣子结构的区间021435–240513∈S6的说明。受先前工作启发的子图以红色突出显示,超立方体以绿色突出显示,分解分量同构于SN-1中的区间以蓝色突出显示。
纽结作为低维拓扑中的基本对象之一,是一个嵌入三维空间的扭曲环。纽结理论可帮助数学家理解纽结的特性以及它与其他数学分支的关系,在生物、物理学科中也有无数应用,如理解DNA链、流体动力学等。

诚如Williamson所说,识别有趣模式的任务主要依赖于数学家自己的直觉,Juhász教授也表示:“纯数学家的工作方式是制定猜想并证明这些猜想,从而得出定理。但是,这些猜想从何而来呢?”
DeepMind的研究已证明,在数学直觉思维的指导下,ML提供了一个强大的框架,在有大量可用数据的领域,或者对象太大而无法应用经典方法研究的领域,可以帮助数学家发现有趣且可证明的猜想。
2
AI在「数学界」大有用武之地
2016年3月,AlphaGo与围棋世界冠军、职业九段棋手李世乭进行围棋人机大战,以4比1的总比分获胜。随后AlphaGo在围棋界取得了一连串紧锣密鼓的胜利,但其背后的DeepMind团队曾表示AlphaGo仅仅是他们AI项目的一个分支。
在未来,DeepMind将一直秉承的理念是:用人工智能解决一切重大科学问题。
基础数学无疑属于重大科学问题的范畴。正如Geordie Williamson教授所说:“数学问题一度被认为是最具智力挑战性的问题……虽然数学家们已经使用ML来帮助分析复杂的数据集,但这是我们第一次使用计算机来辅助形成猜想,或为数学中未经证实的想法提出可能的突破路线。”

图注:Geordie Williamson教授
Geordie Williamson教授是悉尼大学数学研究所所长,也是世界上最重要的数学家之一,在纯数学领域有着非凡的成绩,是全球公认的表象理论的领导者。作为此次论文的合著者,他运用AI在其专业领域成功展开大胆的探索猜想。
论文的一作Alex Davies博士也表示:AI技术已足够先进,足以有力推动许多不同学科的进步。其中,纯数学就是一个典例。团队的研究人员希望,这篇论文能给其他学者带来灵感和启发,充分认识AI在其领域中的潜力。
可见,人工智能在如今的数学研究中已展现出巨大的潜力。追溯历史,计算机科学在数学史上的贡献也是功不可没。
上世纪五十年代,美国华裔数学家王浩等人利用计算机研究罗素和怀德海的名著《数学原理》中定理的证明,成果突出。从上世纪七十年代后期开始,我国数学家吴文俊、张景中等,着手用计算机证明几何定理,在国际上产生了巨大影响。

图注:华裔数学家王浩
1878年6月13日英国数学家凯莱在数学会上正式提出了四色猜想,然后,对四色猜想的证明就如火如荼地展开了,但由于没有大数学家的参与和人工算力的局限,俄罗斯数学家闵科夫斯曾在演算失败后感叹:上帝在惩罚闵科夫斯基的狂妄。其难度可见一斑。1976年,两个美国人阿贝尔和哈肯终于用计算机证明了四色猜想,此举立刻得到社会上的认可,1976年美国伊利诺地方的邮戳上甚至印有纪念文字:“Four colors surfice”。
被誉为「数学世界亚历山大」的德国数学家大卫 · 希尔伯特曾提出23个问题,其中多数已得到完整解决或部分解决。120年后的今天,杜克大学教授 Samit Dasgupta和印度科学研究院教授 Mahesh Kakde终于在计算机程序的助力下找到数字系统的构建块,完美证明了第十二个数学难题“一般代数数域的阿贝尔扩张”。
多年来,数学家一直使用计算机生成数据,以帮助寻找模式。这种被称为实验数学的研究产生了著名的猜想,如Birch和Swinnerton-Dyer猜想——六个“千禧年大奖难题”之一,是数学中最著名的开放性问题(每个问题的奖金都高达一百万美元)。
虽然这种方法已成功实践并且变得相当普遍,但从这些数据中识别和发现模式仍然主要依靠数学家。
在纯数学中,现在生成的数据可能比任何数学家一生所能合理预期的要多,因此,发现模式变得愈加重要。一些感兴趣的物体,比如那些具有数千维空间的物体可能因为太深不可测而无法直接推理,考虑到这些限制,DeepMind团队相信人工智能将能够以全新的方式增强数学家的洞察力。
参考资料:
https://www.nature.com/articles/d41586-021-03593-1
https://mp.weixin.qq.com/s/iPjIemHKHenyvtaUTESRig
https://www.nature.com/articles/s41586-021-04086-x
https://www.leiphone.com/category/academic/uOmvQDxfp64OhOKU.html
https://deepmind.com/blog/article/exploring-the-beauty-of-pure-mathematics-in-novel-ways
未来智能实验室的主要工作包括:建立AI智能系统智商评测体系,开展世界人工智能智商评测;开展互联网(城市)大脑研究计划,构建互联网(城市)大脑技术和企业图谱,为提升企业,行业与城市的智能水平服务。每日推荐范围未来科技发展趋势的学习型文章。目前线上平台已收藏上千篇精华前沿科技文章和报告。
如果您对实验室的研究感兴趣,欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”




















