概率论

在自然语言处理中，以句子为处理单位时一般假设句子独立于它前面的其它语句，句子的概率分布近似地符合二项式分布
贝叶斯决策：
max p(x|w1)p(w1)—x可以是语音信号，而w1可以是我们希望得到的对应文字

信息论


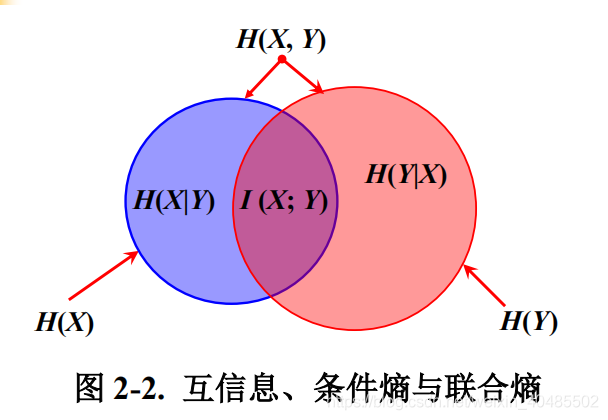
熵(自信息）	$H(X)=−Σx∈Xp(x)log2p(x)=I(X;X)H(X)=-\Sigma_{x\in X}p(x)log_2p(x)=I(X;X)$	熵越大，不确定性越大，越难分类
联合熵	$H(X,Y)=H(X)+H(Y∥X)=−Σx∈XΣy∈Yp(x,y)log2p(x,y)H(X,Y)=H(X)+H(Y\\|X)=-\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)log_2p(x,y)$	描述一对随机变量平均所需要的信息量
条件熵	$H(Y∥X)=Σx∈Xp(x)H(Y∥X=x)=−Σx∈XΣy∈Yp(x,y)log2p(y∥x)H(Y\\|X)=\Sigma_{x\in X}p(x)H(Y\\|X=x)=-\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)log_2p(y\\|x)$	-
熵率	$Hrate=1nH(X1n)=−1nΣX1np(x1n)logp(x1n)H_{rate}=\frac{1}{n}H(X_{1n})=-\frac{1}{n}\Sigma_{X_{1n}}p(x_{1n})logp(x_{1n})$	-
相对熵（KL距离）	$D(p∥q)=Σx∈Xp(x)logp(x)q(x)yD(p\\|q)=\Sigma_{x\in X}p(x)log\frac{p(x)}{q(x)}y$	衡量两个分布的差距，两个随机分布相同则为0，差别增大，则增大
交叉熵	$H(L,q)=−limn→∞1nΣx1np(x1n)logq(x1n)=−limn→∞1Nlogq(x1n)=H(X)+D(p∥q)H(L,q)=-lim_{n\rightarrow \infty}\frac{1}{n}\Sigma_{x_1^n}p(x_1^n)logq(x_1^n)\\=-lim_{n\rightarrow \infty}\frac{1}{N}logq(x_1^n)=H(X)+D(p\\|q)$	在设计模型q时，我们的目的是使交叉熵最小，从而使模型最接近真实的概率分布
困惑度	$PPq=2H(L,q)≈2−12logq(l1n)PP_q=2^{H(L,q)}\approx2^{-\frac{1}{2}logq(l_1^n)}$
互信息	$I(X;Y)=H(X)−H(X∥Y)=Σx∈XΣy∈Yp(x,y)log2p(x,y)p(x)p(y)I(x;y)=logp(x,y)p(x)p(y)=log2p(y∥x)p(y)I(X;Y)=H(X)-H(X\\|Y)\\=\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)log_2\frac{p(x,y)}{p(x)p(y)}\\I(x;y)=log\frac{p(x,y)}{p(x)p(y)}=log_2\frac{p(y\\|x)}{p(y)}$	互信息大，说明两个文字之间的结合越紧密，越可能成词。反之，断开的可能性越大(考虑了两词不连续的情况
耦合度	$couple(ci,ci+1)=N(cici+1)N(cici+1+N(....ci∥ci+1....couple(c_i,c_{i+1})=\frac{N(c_ic_{i+1})}{N(c_ic_{i+1}+N(....c_i\\|c_{i+1}....}$	仅考虑两词连续的情况

熵： $H(X)=−Σx∈Xp(x)log2p(x)H(X)=-\Sigma_{x\in X}p(x)log_2p(x)$
- 约定： $0 l o g 0 = 0$
- 单位：比特（bit）
- 越大，不确定性大，正确估值的可能性小
- 又叫自信息：H(X)=H(X)-H(X|X)=I(X;X)—H(X|X)=0
- 熵又称为自信息(self-information)，表示信源 X 每发一个符号(不论发什么符号)所提供的平均信息量。熵也可以被视为描述一个随机变量的不确定性的数量。一个随机变量的熵越大，它的不确定性越大。那么，正确估计其值的可能性就越小。越不确定的随机变量越需要大的信息量用以确定其值。
联合熵 $H(X,Y)=−Σx∈XΣy∈Yp(x,y)log2p(x,y)=−Σx∈XΣy∈Yp(x,y)log2p(x)p(y∣x)=−Σx∈XΣy∈Yp(x,y)(log2p(x)+log2p(y∣x))=−Σx∈XΣy∈Yp(x,y)(log2p(x))−Σx∈XΣy∈Yp(x,y)(log2p(y∣x))=−Σx∈Xp(x)(log2p(x))−Σx∈XΣy∈Yp(x,y)(log2p(y∣x))=H(X)+H(Y∣X)H(X,Y)=-\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)log_2p(x,y)\\=-\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)log_2p(x)p(y|x)=-\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)(log_2p(x)+log_2p(y|x))=-\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)(log_2p(x))-\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)(log_2p(y|x))\\=-\Sigma_{x\in X}p(x)(log_2p(x))-\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)(log_2p(y|x))\\=H(X)+H(Y|X)$
- 联合熵实际上就是描述一对随机变量平均所需要的信息量。
条件熵 $H(Y∣X)=Σx∈Xp(x)H(Y∣X=x)=Σx∈Xp(x)(−Σy∈Yp(y∣x)log2p(y∣x))=−Σx∈XΣy∈Yp(x,y)log2p(y∣x)H(Y|X)=\Sigma_{x\in X}p(x)H(Y|X=x)\\=\Sigma_{x\in X}p(x)(-\Sigma_{y\in Y}p(y|x)log_2p(y|x))\\=-\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)log_2p(y|x)$
熵率
- 一般地，对于一条长度为 n 的信息，每一个字符或字的熵为： $Hrate=1nH(X1n)=−1nΣX1np(x1n)logp(x1n)H_{rate}=\frac{1}{n}H(X_{1n})=-\frac{1}{n}\Sigma_{X_{1n}}p(x_{1n})logp(x_{1n})$
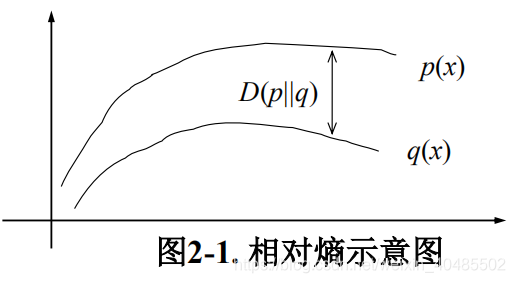
相对熵（KL距离）
- $D(p∣∣q)=Σx∈Xp(x)logp(x)q(x)约定0log(0/q)=0,plog(p/0)=∞D(p||q)=\Sigma_{x\in X}p(x)log\frac{p(x)}{q(x)}\\约定0log(0/q)=0,plog(p/0)=\infty$
- 用来：衡量两个分布的差距，两个随机分布相同则为0，差别增大，则增大
交叉熵
- 随机变量X`p(x)，模型q
- 用以衡量估计模型与真实概率分布之间的差异
- $H(X,q)=H(X)+D(p∣∣q)=−Σxp(x)logq(x)H(X,q)=H(X)+D(p||q)=-\Sigma_xp(x)logq(x)$
- 对于语言L=(X)-p(x)与其模型q的交叉熵定义为
  - $H(L,q)=−limn→∞1nΣx1np(x1n)logq(x1n)H(L,q)=-lim_{n\rightarrow \infty}\frac{1}{n}\Sigma_{x_1^n}p(x_1^n)logq(x_1^n)$
  - p(x_1^n)概率
  - q(x_1^n)为概率估计值（频率）
  - 如果是理想的语言，n趋于无穷大（记做N),假定L是稳态的随机过程
  - $H(L,q)=−limn→∞1nΣx1np(x1n)logq(x1n)=−limn→∞1Nlogq(x1n)H(L,q)=-lim_{n\rightarrow \infty}\frac{1}{n}\Sigma_{x_1^n}p(x_1^n)logq(x_1^n)\\=-lim_{n\rightarrow \infty}\frac{1}{N}logq(x_1^n)$
  - 在设计模型q时，我们的目的是使交叉熵最小，从而使模型最接近真实的概率分布
困惑度
- 再设计语言模型时，可以用困惑度来代替交叉熵衡量模型的好坏
- 语言L的样本 $l1n=l1...lnPPq=2H(L,q)≈2−12logq(l1n)l_1^n=l_1...l_n\\PP_q=2^{H(L,q)}\approx2^{-\frac{1}{2}logq(l_1^n)}$
互信息
- （X,Y)-P(x,y）
- $I(X;Y)=H(X)−H(X∣Y)=Σx∈XΣy∈Yp(x,y)log2p(x,y)p(x)p(y)I(x;y)=logp(x,y)p(x)p(y)=log2p(y∣x)p(y)I(X;Y)=H(X)-H(X|Y)\\=\Sigma_{x\in X}\Sigma_{y\in Y}p(x,y)log_2\frac{p(x,y)}{p(x)p(y)}\\I(x;y)=log\frac{p(x,y)}{p(x)p(y)}=log_2\frac{p(y|x)}{p(y)}$
- 互信息 I (X; Y) 是在知道了 Y 的值以后 X 的不确定性的减少量，即Y 的值透露了多少关于 X 的信息量。
- 又叫自信息：H(X)=H(X)-H(X|X)=I(X;X)—H(X|X)=0
- 说明两个完全依赖的变量之间的互信息并不是一个常量，而是取决于他俩之间的熵
- 互信息大，说明两个文字之间的结合越紧密，越可能成词。反之，断开的可能性越大
  - 关系强：I(x;y)>0
  - 弱： $I(x;y)≈0I(x;y)\approx0$
  - 互补分布：I(x;y)<0
- 两个单个离散事件(xi, yj)之间的互信息I(xi, yj)可
  能为负值，但
- 两个随机变量(X, Y)之间的互信息I(X, Y)不可能为负值。后者通常称为平均互信息
耦合度
- $couple(ci,ci+1)=N(cici+1N(cici+1+N(....ci∣ci+1....couple(c_i,c_{i+1})=\frac{N(c_ic_{i+1}}{N(c_ic_{i+1}+N(....c_i|c_{i+1}....}$
- 两字相邻的情况
  - 相邻且是一个词
  - 相邻但不是一个词
  - 不相邻（耦合度不考虑这个情况，但互信息考虑）
    - 有些汉字在实际应用中出现虽然比较频繁，但是连续在一起出现的情况比较少，一旦连在一起出现，就很可能是一个词。这种情况下计算出来的互信息会比较小，而实际上两者的结合度应该是比较高的。而双字耦合度恰恰计算的是两个连续汉字出现在一个词中的概率，并不考虑两个汉字非连续出现的情况。

计算熵

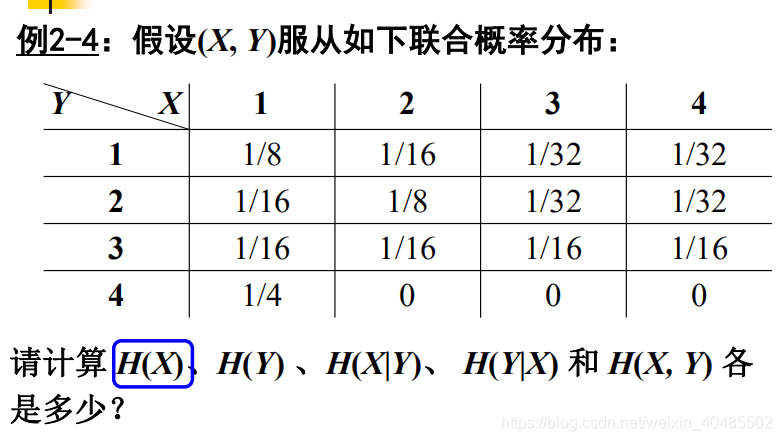
在这里插入图片描述

计算信息熵、条件熵、联合熵

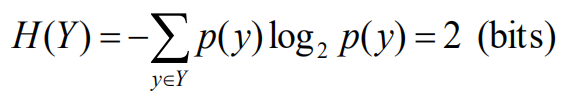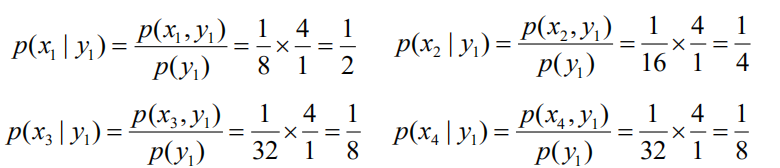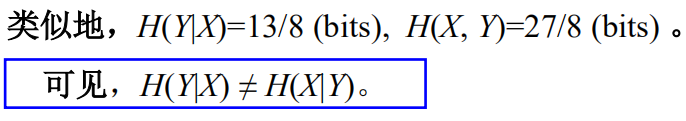
在这里插入图片描述 ))))

波利尼亚语

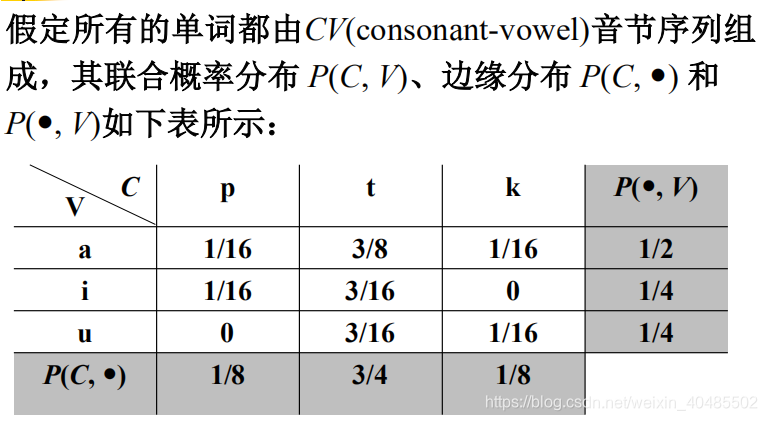
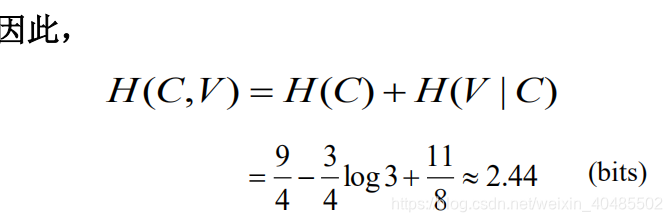
在这里插入图片描述

熵率

在这里插入图片描述

噪声信道模型

要求：在信号传输的过程中都要进行双重性处理：
- 一方面要通过压缩消除所有的冗余，
- 另一方面又要通过增加一定的可控冗余以保障输入信号经过噪声信道后可以很好地恢复原状。
- 信息编码时要尽量占用少量的空间，
- 但又必须保持足够的冗余以便能够检测和校验错误。
- 接收到的信号需要被解码使其尽量恢复到原始的输入信号。
目标：就是优化噪声信道中信号传输的吞吐量和准确率，其
基本假设：是一个信道的输出以一定的概率依赖于输入。
信道容量(capacity)：其基本思想是用降低传输速率来换取高保真通讯的可能性。其定义可以根据互信息给出
- $C=max_{p(x)}I(X;Y)$
- 据此定义，如果我们能够设计一个输入编码 X，其概率分布为 p(X)，使其输入与输出之间的互信息达到最大值，那么，我们的设计就达到了信道的最大传输容量。
在语言处理中，我们不需要进行编码，只需要进行解码，使系统的输出更接近于输入，如机器翻译。（自编码器）
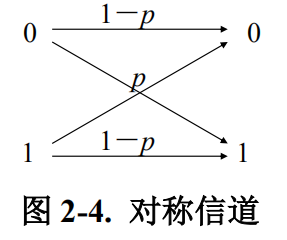
一个二进制的对称信道 (binary symmetric channel, BSC) 的输入符号集 X:{0, 1}，输出符号集Y:{0, 1}。在传输过程中如果输入符号被误传的概率为 p，那么，被正确传输的概率就是 1－p。这个过程我们可以用一个对称的图型表示如下：

建立一个翻译

估计语言模型p(e)
估计翻译模型p(f|e)
设计快速有效的搜索算法求解e使得p(e)p(f|e)最大

词义消歧（WSD

定义：任何一种自然语言中，一词多义（歧义）现象
是普遍存在的。如何区分不同上下文中的词汇语义，
就是词汇歧义消解问题，或称词义消歧(word sense
disambiguation, WSD) 。
- 一个基本问题
基本思路：依据上下文
- 每个词表达不同的含意时其上下文（语境）往往不同，也就是说，不同的词义对应不同的上下文，因此，如果能够将多义词的上下文区别开，其词义自然就明确了。
- 基本的上下文信息：词，词性，位置
基于上下文分类的消除歧义方法
- 基于贝叶斯分类器
- 最大熵的消歧方法

贝叶斯

假设某个多义词 w 所处的上下文语境为 C，如果w 的多个语义记作 si，那么，可通过计算 argmaxp(si|C)确定w 的词义
$p(si∣C)=p(si)p(C∣si)p(C)分母不变性，及独立性假设：P(C∣si)=Πck∈Cp(ck∣si)所以，si^=argmaxsi(p(si)Πck∈Cp(ck∣si))−−极大似然估计得到：p(ck∣si)=N(ck,si）N(si)−−出现次数p(si)=N(si)N(w)−−N(w)为多义词w总共出现的次数p(s_i|C)=\frac{p(s_i)p(C|s_i)}{p(C)}\\分母不变性，及独立性假设：P(C|s_i)=\Pi_{c_k\in C}p(c_k|s_i)\\所以，\hat{s_i}=argmax_{s_i}(p(s_i)\Pi_{c_k\in C}p(c_k|s_i))--极大似然估计得到：\\p(c_k|s_i)=\frac{N(c_k,s_i）}{N(s_i)}--出现次数\\p(s_i)=\frac{N(s_i)}{N(w)}--N(w)为多义词w总共出现的次数$
实际，用对数计算
- $si^=argmax(logp(si)+Σck∈Clogp(ck∣si)\hat{s_i}=argmax(logp(s_i)+\Sigma_{c_k\in C}logp(c_k|s_i)$
算法描述
1. 训练过程：
  1. 计算 $p(ck∣si)=N(ck,si）N(si)−−出现次数p(c_k|s_i)=\frac{N(c_k,s_i）}{N(s_i)}--出现次数$
  2. 计算 $p(si)=N(si)N(w)p(s_i)=\frac{N(s_i)}{N(w)}$
2. 预测过程：
  - $si^=argmax(logp(si)+Σck∈Clogp(ck∣si)\hat{s_i}=argmax(logp(s_i)+\Sigma_{c_k\in C}logp(c_k|s_i)$
例子
对于“打”字而言，假设做实词用的25个语义分别标
记为：s1 ~ s25，两个虚词语义分别标记为： s26 、s27。
假设 s1 的语义为“敲击(beat)”。那么，N(s1)表示“打”
字的意思为“敲击(beat)”时在所有统计样本中出现的
次数；N(ck, s1) 表示某个词 ck 出现在 s1 的上下文中时
出现的次数。例如，句子：对于“打”字而言，假设做实词用的25个语义分别标记为：s1 ~ s25，两个虚词语义分别标记为： s26 、s27。假设 s1 的语义为“敲击(beat)”。那么，N(s1)表示“打”字的意思为“敲击(beat)”时在所有统计样本中出现的次数；N(ck, s1) 表示某个词 ck出现在 s1 的上下文中时出现的次数。例如，句子：
上下文C=(他，对，鼓，很），ck=他，N(他，s1)=5,N(s1)=100
p(ck|si)=p(他|s1)=5/100=0.05
p(s1)=N(s1)/N(w)=100/800=0.125

最大熵的消歧方法

基本思想：在只掌握关于未知分布的部分知识的情况下，符合已知知识的概率分布可能有多个，但使熵值最大的概率分布最真实地反映了事件的分布情况，因为熵定义了随机变量的不确定性，当熵最大时，随机变量最不确定。也就是说，在已知部分知识的前提下，关于未知分布最合理的推断应该是符合已知知识最不确定或最大随机的推断。
对于求解的问题，就是估计在条件b ∈B下(已知知识) ，发生某个事件(未知分布) 的概率p(a|b)，该概率使熵 H(p(A|B))最大。
用最随机情况下的概率来推导
上下文条件b表示有：
- 词形
- 词性
- 词形+词性
两种表示方法
- 位置有关（模板表示
- 位置无关（词袋模型
$EP(f)=Σa,bp~(b)p(a∣b)f(a,b)希望（约束）EP(f)=EP~(f),EP~(f)=Σa,bp~(a,b)f(a,b)C={p∈Γ∣EP(f)=EP~(f)}所以，H(p)=L(p)=−Σa,bp~(b)p(a∣b)log(p(a∣b))p∗(a∣b)=argmaxpH(p)E_P(f)=\Sigma_{a,b}\tilde{p}(b)p(a|b)f(a,b)\\希望（约束）E_P(f)=E_{\tilde{P}}(f),\\E_{\tilde{P}}(f)=\Sigma_{a,b}\tilde{p}(a,b)f(a,b)\\C=\{p\in \Gamma |E_P(f)=E_{\tilde{P}}(f)\}\\所以，H(p)=L(p)=-\Sigma_{a,b}\tilde{p}(b)p(a|b)log(p(a|b))\\p^*(a|b)=argmax_p H(p)$
确定特征函数