前言

当我们要训练一个已经写好的神经网络时，我们就要直面诸多的超参数了。这些超参数一旦选不好，那么很有可能让神经网络跑的还不如感知机。因此在面对神经网络这种容量很大的model前，是很有必要深刻的理解一下各个超参数的意义及其对model的影响的。

回顾

简单回顾一下神经网络的一次迭代过程：

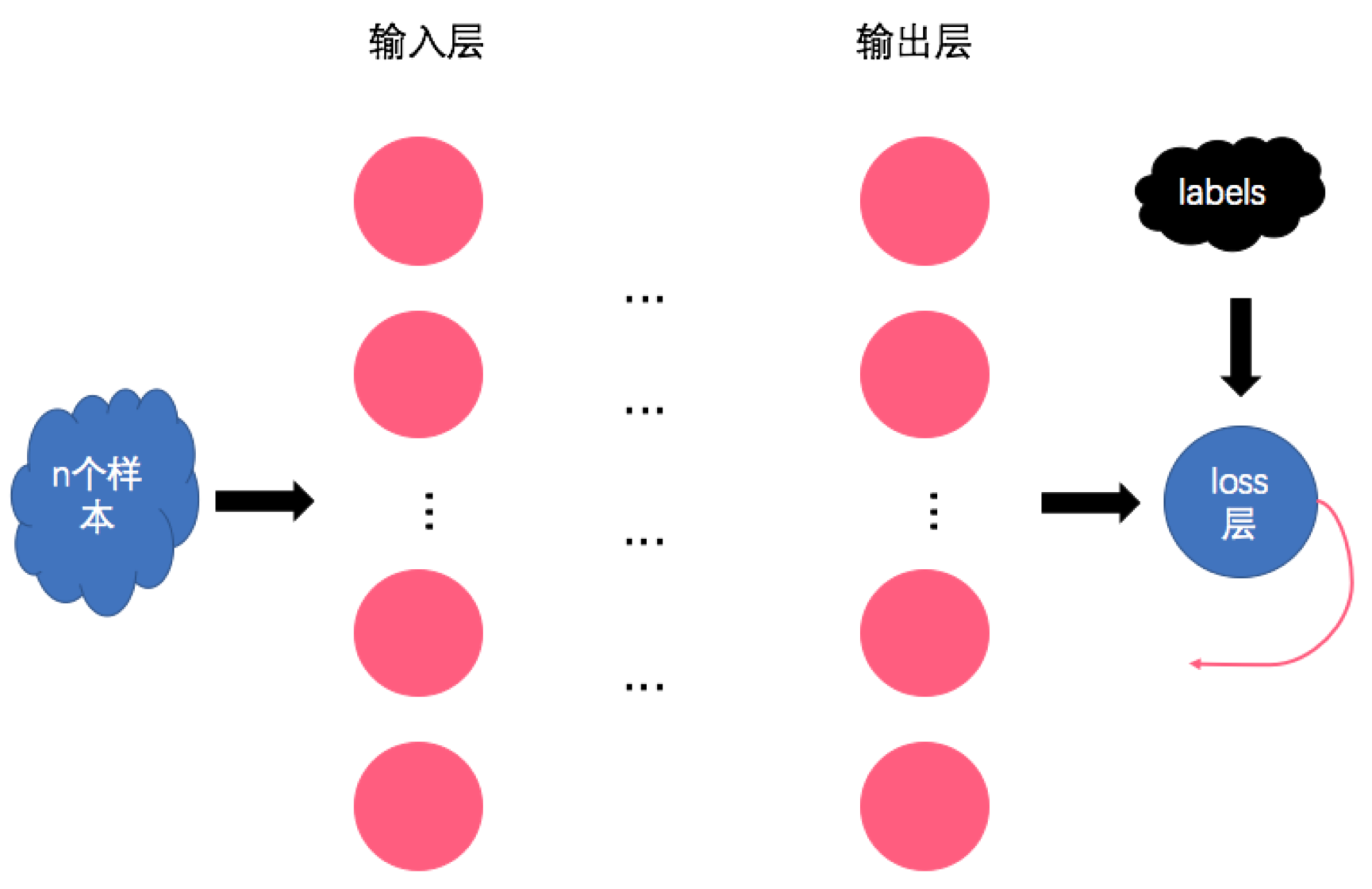
即，首先选择n个样本组成一个batch，然后将batch丢进神经网络，得到输出结果。再将输出结果与样本label丢给loss函数算出本轮的loss，而后就可以愉快的跑BP算法了（从后往前逐层计算参数之于loss的导数）。最后将每个参数的导数配合步长参数来进行参数更新。这就是训练过程的一次迭代。

Batch Size

由此，最直观的超参数就是batch的大小——我们可以一次性将整个数据集喂给神经网络，让神经网络利用全部样本来计算迭代时的梯度（即传统的梯度下降法），也可以一次只喂一个样本（即随机梯度下降法，也称在线梯度下降法），也可以取个折中的方案，即每次喂一部分样本让其完成本轮迭代（即batch梯度下降法）。

数学基础不太好的初学者可能在这里犯迷糊——一次性喂500个样本并迭代一次，跟一次喂1个样本迭代500次相比，有区别吗？

其实这两个做法就相当于：

第一种：
total = 旧参下计算更新值1+旧参下计算更新值2+...+旧参下计算更新值500 ;
新参数 = 旧参数 + total

第二种：
新参数1 = 旧参数 + 旧参数下计算更新值1；
新参数2 = 新参数1 + 新参数1下计算更新值1；
新参数3 = 新参数2 + 新参数2下计算更新值1；
...
新参数500 = 新参数500 + 新参数500下计算更新值1；

也就是说，第一种是将参数一次性更新500个样本的量，第二种是迭代的更新500次参数。当然是不一样的啦。

那么问题来了，哪个更好呢？

Which one？

我们首先分析最简单的影响，哪种做法收敛更快呢？

我们假设每个样本相对于大自然真实分布的标准差为σ，那么根据概率统计的知识，很容易推出n个样本的标准差为 （有疑问的同学快翻开概率统计的课本看一下推导过程）。从这里可以看出，我们使用样本来估计梯度的时候，1个样本带来σ的标准差，但是使用n个样本区估计梯度并不能让标准差线性降低（也就是并不能让误差降低为原来的1/n，即无法达到σ/n），而n个样本的计算量却是线性的（每个样本都要平等的跑一遍前向算法）。

由此看出，显然在同等的计算量之下（一定的时间内），使用整个样本集的收敛速度要远慢于使用少量样本的情况。换句话说，要想收敛到同一个最优点，使用整个样本集时，虽然迭代次数少，但是每次迭代的时间长，耗费的总时间是大于使用少量样本多次迭代的情况的。

那么是不是样本越少，收敛越快呢？

理论上确实是这样的，使用单个单核cpu的情况下也确实是这样的。但是我们要与工程实际相结合呀~实际上，工程上在使用GPU训练时，跑一个样本花的时间与跑几十个样本甚至几百个样本的时间是一样的！当然得益于GPU里面超多的核，超强的并行计算能力啦。因此，在工程实际中，从收敛速度的角度来说，小批量的样本集是最优的，也就是我们所说的mini-batch。这时的batch size往往从几十到几百不等，但一般不会超过几千（你有土豪显卡的话，当我没说）。

那么，如果我真有一个怪兽级显卡，使得一次计算10000个样本跟计算1个样本的时间相同的话，是不是设置10000就一定是最好的呢？虽然从收敛速度上来说是的，但！是！

我们知道，神经网络是个复杂的model，它的损失函数也不是省油的灯，在实际问题中，神经网络的loss曲面（以model参数为自变量，以loss值为因变量画出来的曲面）往往是非凸的，这意味着很可能有多个局部最优点，而且很可能有鞍点！

插播一下，鞍点就是loss曲面中像马鞍一样形状的地方的中心点，如下图：

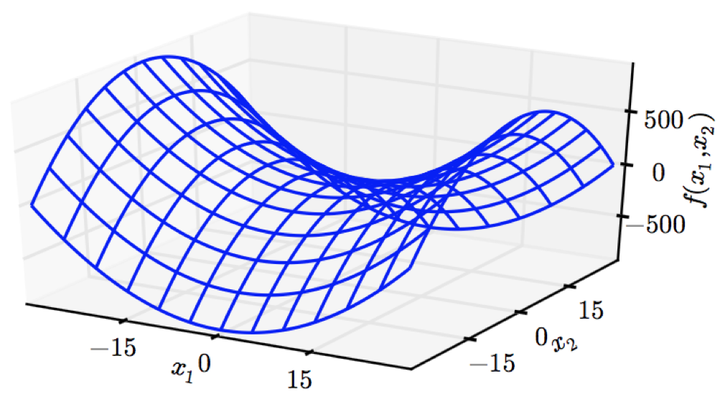（图片来自《Deep Learning》）

想象一下，在鞍点处，横着看的话，鞍点就是个极小值点，但是竖着看的话，鞍点就是极大值点（线性代数和最优化算法过关的同学应该能反应过来，鞍点处的Hessian矩阵的特征值有正有负。不理解也没关系，小夕过几天就开始写最优化的文章啦~），因此鞍点容易给优化算法一个“我已经收敛了”的假象，殊不知其旁边有一个可以跳下去的万丈深渊。。。（可怕）

回到主线上来，小夕在《机器学习入门指导（4）》中提到过，传统的最优化算法是无法自动的避开局部最优点的，对于鞍点也是理论上很头疼的东西。但是实际上，工程中却不怎么容易陷入很差劲的局部最优点或者鞍点，这是为什么呢？

暂且不说一些很高深的理论如“神经网络的loss曲面中的局部最优点与全局最优点差不太多”，我们就从最简单的角度想~

想一想，样本量少的时候会带来很大的方差，而这个大方差恰好会导致我们在梯度下降到很差的局部最优点（只是微微凸下去的最优点）和鞍点的时候不稳定，一不小心就因为一个大噪声的到来导致炸出了局部最优点，或者炸下了马（此处请保持纯洁的心态！），从而有机会去寻找更优的最优点。

因此，与之相反的，当样本量很多时，方差很小（咦？最开始的时候好像在说标准差来着，反正方差与标准差就差个根号，没影响的哈~），对梯度的估计要准确和稳定的多，因此反而在差劲的局部最优点和鞍点时反而容易自信的呆着不走了，从而导致神经网络收敛到很差的点上，跟出了bug一样的差劲。

小总结一下，batch的size设置的不能太大也不能太小，因此实际工程中最常用的就是mini-batch，一般size设置为几十或者几百。但是！

好像这篇文章的转折有点多了诶。。。

细心的读者可能注意到了，这之前我们的讨论是基于梯度下降的，而且默认是一阶的（即没有利用二阶导数信息，仅仅使用一阶导数去优化）。因此对于SGD（随机梯度下降）及其改良的一阶优化算法如Adagrad、Adam等是没问题的，但是对于强大的二阶优化算法如共轭梯度法、L-BFGS来说，如果估计不好一阶导数，那么对二阶导数的估计会有更大的误差，这对于这些算法来说是致命的。

因此，对于二阶优化算法，减小batch换来的收敛速度提升远不如引入大量噪声导致的性能下降，因此在使用二阶优化算法时，往往要采用大batch哦。此时往往batch设置成几千甚至一两万才能发挥出最佳性能。

另外，听说GPU对2的幂次的batch可以发挥更佳的性能，因此设置成16、32、64、128...时往往要比设置为整10、整100的倍数时表现更优（不过我没有验证过，有兴趣的同学可以试验一下~

参考文献《Deep Learning》

本文转载自微信订阅号【夕小瑶的卖萌屋】，听说每个想学机器学习的人到这里都停不下来了~