版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/taoyanqi8932/article/details/53727841 </div><link rel="stylesheet" href="https://csdnimg.cn/release/phoenix/template/css/ck_htmledit_views-f57960eb32.css"><div id="content_views" class="markdown_views"><!-- flowchart 箭头图标 勿删 --><svg xmlns="http://www.w3.org/2000/svg" style="display: none;"><path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block" style="-webkit-tap-highlight-color: rgba(0, 0, 0, 0);"></path></svg><h2 id="概述"><a name="t0"></a><strong>概述</strong></h2>
什么是聚类分析
聚类分析是在数据中发现数据对象之间的关系,将数据进行分组,组内的相似性越大,组间的差别越大,则聚类效果越好。
不同的簇类型
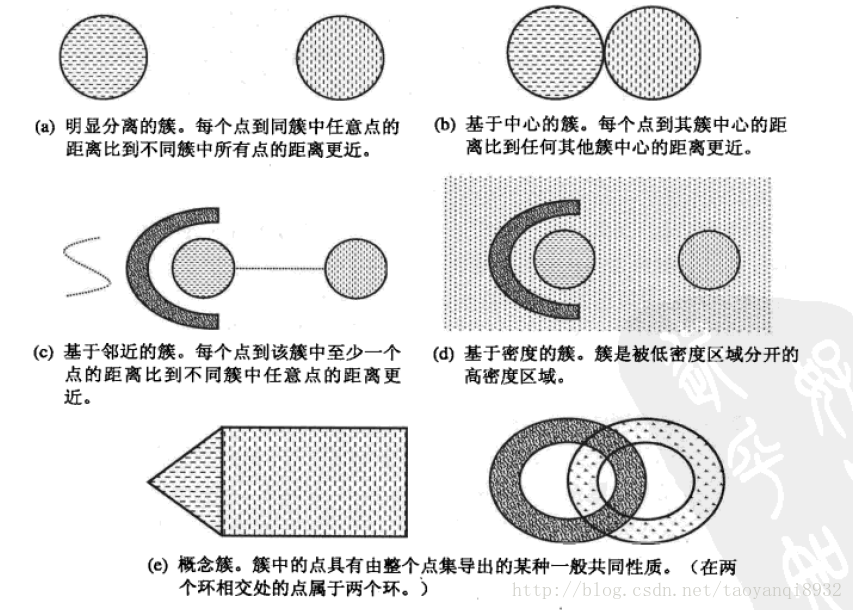
聚类旨在发现有用的对象簇,在现实中我们用到很多的簇的类型,使用不同的簇类型划分数据的结果是不同的,如下的几种簇类型。
明显分离的
可以看到(a)中不同组中任意两点之间的距离都大于组内任意两点之间的距离,明显分离的簇不一定是球形的,可以具有任意的形状。
基于原型的
簇是对象的集合,其中每个对象到定义该簇的原型的距离比其他簇的原型距离更近,如(b)所示的原型即为中心点,在一个簇中的数据到其中心点比到另一个簇的中心点更近。这是一种常见的基于中心的簇,最常用的K-Means就是这样的一种簇类型。
这样的簇趋向于球形。
基于密度的
簇是对象的密度区域,(d)所示的是基于密度的簇,当簇不规则或相互盘绕,并且有早上和离群点事,常常使用基于密度的簇定义。
关于更多的簇介绍参考《数据挖掘导论》。
基本的聚类分析算法
1. K均值:
基于原型的、划分的距离技术,它试图发现用户指定个数(K)的簇。
2. 凝聚的层次距离:
思想是开始时,每个点都作为一个单点簇,然后,重复的合并两个最靠近的簇,直到尝试单个、包含所有点的簇。
3. DBSCAN:
一种基于密度的划分距离的算法,簇的个数有算法自动的确定,低密度中的点被视为噪声而忽略,因此其不产生完全聚类。
距离量度
不同的距离量度会对距离的结果产生影响,常见的距离量度如下所示:
K-Means算法
下面介绍K均值算法:
优点:易于实现
缺点:可能收敛于局部最小值,在大规模数据收敛慢
算法思想较为简单如下所示:
选择K个点作为初始质心
repeat 将每个点指派到最近的质心,形成K个簇 重新计算每个簇的质心
until 簇不发生变化或达到最大迭代次数 - 1
- 2
- 3
- 4
- 5
这里的重新计算每个簇的质心,如何计算的是根据目标函数得来的,因此在开始时我们要考虑距离度量和目标函数。
考虑欧几里得距离的数据,使用误差平方和(Sum of the Squared Error,SSE)作为聚类的目标函数,两次运行K均值产生的两个不同的簇集,我们更喜欢SSE最小的那个。
k表示k个聚类中心,ci表示第几个中心,dist表示的是欧几里得距离。
这里有一个问题就是为什么,我们更新质心是让所有的点的平均值,这里就是SSE所决定的。
下面用Python进行实现
# dataSet样本点,k 簇的个数
# disMeas距离量度,默认为欧几里得距离
# createCent,初始点的选取
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):m = shape(dataSet)[0] #样本数clusterAssment = mat(zeros((m,2))) #m*2的矩阵 centroids = createCent(dataSet, k) #初始化k个中心clusterChanged = True while clusterChanged: #当聚类不再变化clusterChanged = Falsefor i in range(m):minDist = inf; minIndex = -1for j in range(k): #找到最近的质心distJI = distMeas(centroids[j,:],dataSet[i,:])if distJI < minDist:minDist = distJI; minIndex = jif clusterAssment[i,0] != minIndex: clusterChanged = True# 第1列为所属质心,第2列为距离clusterAssment[i,:] = minIndex,minDist**2print centroids# 更改质心位置for cent in range(k):ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]centroids[cent,:] = mean(ptsInClust, axis=0) return centroids, clusterAssment- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
重点理解一下:
for cent in range(k):ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]centroids[cent,:] = mean(ptsInClust, axis=0) - 1
- 2
- 3
循环每一个质心,找到属于当前质心的所有点,然后根据这些点去更新当前的质心。
nonzero()返回的是一个二维的数组,其表示非0的元素位置。
>>> from numpy import *
>>> a=array([[1,0,0],[0,1,2],[2,0,0]])
>>> a
array([[1, 0, 0],[0, 1, 2],[2, 0, 0]])
>>> nonzero(a)
(array([0, 1, 1, 2]), array([0, 1, 2, 0]))- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
表示第[0,0],[1,1] … 位非零元素。第一个数组为行,第二个数组为列,两者进行组合得到的。
ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]
因此首先先比较clusterAssment[:,0].A==cent的真假,如果为真则记录了他所在的行,因此在用切片进行取值。
一些辅助的函数:
def loadDataSet(fileName): #general function to parse tab -delimited floatsdataMat = [] #assume last column is target valuefr = open(fileName)for line in fr.readlines():curLine = line.strip().split('\t')fltLine = map(float,curLine) #map all elements to float()dataMat.append(fltLine)return dataMatdef distEclud(vecA, vecB):return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)def randCent(dataSet, k):n = shape(dataSet)[1]centroids = mat(zeros((k,n)))#create centroid matfor j in range(n):#create random cluster centers, within bounds of each dimensionminJ = min(dataSet[:,j]) rangeJ = float(max(dataSet[:,j]) - minJ)centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))return centroids- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
运行和结果
将上述代码写到kMeans.py中,然后打开python交互端。
>>> from numpy import *
>>> import kMeans
>>> dat=mat(kMeans.loadDataSet('testSet.txt')) #读入数据
>>> center,clust=kMeans.kMeans(dat,4)
[[ 0.90796996 5.05836784][-2.88425582 0.01687006][-3.3447423 -1.01730512][-0.32810867 0.48063528]]
[[ 1.90508653 3.530091 ][-3.00984169 2.66771831][-3.38237045 -2.9473363 ][ 2.22463036 -1.37361589]]
[[ 2.54391447 3.21299611][-2.46154315 2.78737555][-3.38237045 -2.9473363 ][ 2.8692781 -2.54779119]]
[[ 2.6265299 3.10868015][-2.46154315 2.78737555][-3.38237045 -2.9473363 ][ 2.80293085 -2.7315146 ]]
# 作图
>>>kMeans(dat,center)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
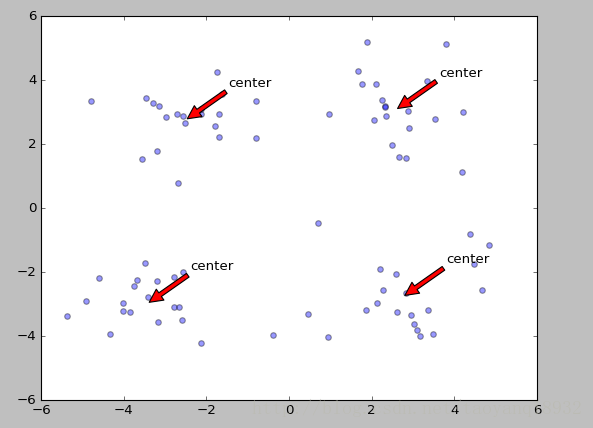
绘图的程序如下:
def draw(data,center):length=len(center)fig=plt.figure# 绘制原始数据的散点图plt.scatter(data[:,0],data[:,1],s=25,alpha=0.4)# 绘制簇的质心点for i in range(length):plt.annotate('center',xy=(center[i,0],center[i,1]),xytext=\(center[i,0]+1,center[i,1]+1),arrowprops=dict(facecolor='red'))plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
K-Means算法的缺陷
k均值算法非常简单且使用广泛,但是其有主要的两个缺陷:
1. K值需要预先给定,属于预先知识,很多情况下K值的估计是非常困难的,对于像计算全部微信用户的交往圈这样的场景就完全的没办法用K-Means进行。对于可以确定K值不会太大但不明确精确的K值的场景,可以进行迭代运算,然后找出Cost Function最小时所对应的K值,这个值往往能较好的描述有多少个簇类。
2. K-Means算法对初始选取的聚类中心点是敏感的,不同的随机种子点得到的聚类结果完全不同
3. K均值算法并不是很所有的数据类型。它不能处理非球形簇、不同尺寸和不同密度的簇,银冠指定足够大的簇的个数是他通常可以发现纯子簇。
4. 对离群点的数据进行聚类时,K均值也有问题,这种情况下,离群点检测和删除有很大的帮助。
下面对初始质心的选择进行讨论:
拙劣的初始质心
当初始质心是随机的进行初始化的时候,K均值的每次运行将会产生不同的SSE,而且随机的选择初始质心结果可能很糟糕,可能只能得到局部的最优解,而无法得到全局的最优解。如下图所示:
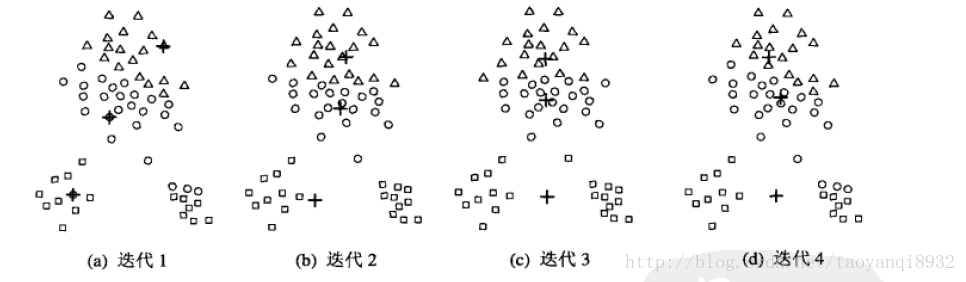
可以看到程序迭代了4次终止,其得到了局部的最优解,显然我们可以看到其不是全局最优的,我们仍然可以找到一个更小的SSE的聚类。
随机初始化的局限
你可能会想到:多次运行,每次使用一组不同的随机初始质心,然后选择一个具有最小的SSE的簇集。该策略非常的简单,但是效果可能不是很好,这取决于数据集合寻找的簇的个数。
关于更多,参考《数据挖掘导论》
K-Means优化算法
为了克服K-Means算法收敛于局部最小值的问题,提出了一种二分K-均值(bisecting K-means)
bisecting K-means
算法的伪代码如下:
将所有的点看成是一个簇
当簇小于数目k时对于每一个簇计算总误差在给定的簇上进行K-均值聚类,k值为2计算将该簇划分成两个簇后总误差选择是的误差最小的那个簇进行划分- 1
- 2
- 3
- 4
- 5
- 6
- 7
完整的Python代码如下:
def biKmeans(dataSet, k, distMeas=distEclud):m = shape(dataSet)[0]# 这里第一列为类别,第二列为SSEclusterAssment = mat(zeros((m,2)))# 看成一个簇是的质心centroid0 = mean(dataSet, axis=0).tolist()[0]centList =[centroid0] #create a list with one centroidfor j in range(m): #计算只有一个簇是的误差clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2# 核心代码while (len(centList) < k):lowestSSE = inf# 对于每一个质心,尝试的进行划分for i in range(len(centList)):# 得到属于该质心的数据ptsInCurrCluster =\ dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]# 对该质心划分成两类centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)# 计算该簇划分后的SSEsseSplit = sum(splitClustAss[:,1])# 没有参与划分的簇的SSEsseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])print "sseSplit, and notSplit: ",sseSplit,sseNotSplit# 寻找最小的SSE进行划分# 即对哪一个簇进行划分后SSE最小if (sseSplit + sseNotSplit) < lowestSSE:bestCentToSplit = ibestNewCents = centroidMatbestClustAss = splitClustAss.copy()lowestSSE = sseSplit + sseNotSplit# 较难理解的部分bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whateverbestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplitprint 'the bestCentToSplit is: ',bestCentToSplitprint 'the len of bestClustAss is: ', len(bestClustAss)centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids centList.append(bestNewCents[1,:].tolist()[0])clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSEreturn mat(centList), clusterAssment- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
下面对最后的代码进行解析:
bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whatever
bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit- 1
- 2
这里是更改其所属的类别,其中bestClustAss = splitClustAss.copy()是进行k-means后所返回的矩阵,其中第一列为类别,第二列为SSE值,因为当k=2是k-means返回的是类别0,1两类,因此这里讲类别为1的更改为其质心的长度,而类别为0的返回的是该簇原先的类别。
举个例子:
例如:目前划分成了0,1两个簇,而要求划分成3个簇,则在算法进行时,假设对1进行划分得到的SSE最小,则将1划分成了2个簇,其返回值为0,1两个簇,将返回为1的簇改成2,返回为0的簇改成1,因此现在就有0,1,2三个簇了。
centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids centList.append(bestNewCents[1,:].tolist()[0])clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSE- 1
- 2
- 3
其中bestNewCents是k-means的返回簇中心的值,其有两个值,分别是第一个簇,和第二个簇的坐标(k=2),这里将第一个坐标赋值给 centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0],将另一个坐标添加到centList中 centList.append(bestNewCents[1,:].tolist()[0])
运行与结果
>>> from numpy import *
>>> import kMeans
>>> dat = mat(kMeans.loadDataSet('testSet2.txt'))
>>> cent,assment=kMeans.biKmeans(dat,3)
sseSplit, and notSplit: 570.722757425 0.0
the bestCentToSplit is: 0
the len of bestClustAss is: 60
sseSplit, and notSplit: 68.6865481262 38.0629506357
sseSplit, and notSplit: 22.9717718963 532.659806789
the bestCentToSplit is: 0
the len of bestClustAss is: 40- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
可以看到进行了两次的划分,第一次最好的划分是在0簇,第二次划分是在1簇。
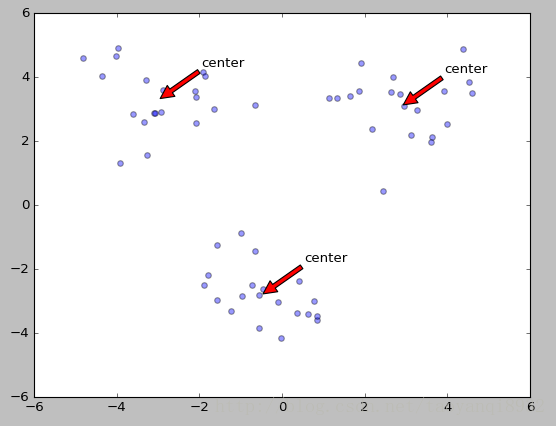
可视化如下图所示:
Mini Batch k-Means
在原始的K-means算法中,每一次的划分所有的样本都要参与运算,如果数据量非常大的话,这个时间是非常高的,因此有了一种分批处理的改进算法。
使用Mini Batch(分批处理)的方法对数据点之间的距离进行计算。
Mini Batch的好处:不必使用所有的数据样本,而是从不同类别的样本中抽取一部分样本来代表各自类型进行计算。n 由于计算样本量少,所以会相应的减少运行时间n 但另一方面抽样也必然会带来准确度的下降。


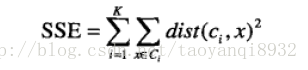




遍历树)




的主要研究方向有哪些?)
及应用)







)

