摘要：主成分分析（英语：Principal components analysis，PCA）是一种分析、简化数据集的技术。主成分分析经常用于减少数据集的维数，同时保持数据集中的对方差贡献最大的特征。常常应用在文本处理、人脸识别、图片识别、自然语言处理等领域。可以做在数据预处理阶段非常重要的一环，本文首先对基本概念进行介绍，然后给出PCA算法思想、流程、优缺点等等。最后通过一个综合案例去实现应用。（本文原创，转载必须注明出处.）

继续阅读 →

逻辑回归模型算法研究与案例分析

(白宁超  2018年9月11日11:37:17)

导读：逻辑回归（Logistic regression）即逻辑模型，属于常见的一种分类算法。本文将从理论介绍开始，搞清楚什么是逻辑回归、回归系数、算法思想、工作原理及其优缺点等。进一步通过两个实际案例深化理解逻辑回归，以及在工程应用进行实现。（本文原创，转载必须注明出处： 决策树模型算法研究与案例分析）

继续阅读 →

当面对众多选择时，如何选才能最大化收益（或者说最小化我们的开销）？比如，怎么选择最优的上班的路线才能使途中花费的时间最少？假设每天上下班路线是确定的，我们便可以在账本中记下往返路线的长度。

A/B测试便是基于数据来进行优选的常用方法，在记录多次上班路线长度后，我们便会从数据中发现到一些模式（例如路线A比路线B花的时间更少），然后最终一致选择某条路线。

当A/B测试遇到非简单情况时（如分组不够随机时，或用户量不够大到可以忽略组间差异，或不希望大规模A/B测试长期影响一部分用户的收益），该怎样通过掌握理论知识来更好的指导实践呢？本文尝试通过由浅入深的介绍，希望能够帮助大家对A/B测试有更加深入的理解。

NO.1

为什么需要A/B测试

任何问题，只要它的每个选项能够被多次进行测试，并且每个选项在被测试时都能返回固定的结果，那么它就能使用A/B测试技术来进行优化。在上述例子中，每天的上下班路线是确定的，所以我们能够在账本中记下往返路线的长度。

那么什么样的路线对于用户来说才是一个好的方案呢？是考虑路线A还是B？什么时候用户才有充分的数据去确定哪条线路是最好的？测试线路好与不好的最优策略又是什么？图1用形式化概括定义了问题。

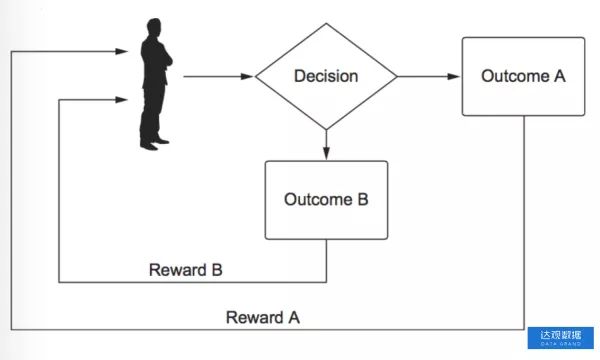
图1 形式化定义的问题

在这个场景中，参与的用户正面临一个选择，根据他的决策会生成一个结果，而这个结果会对应一份给参与者的反馈。假设用户持续地暴露于这个决策，他应该怎么制定获得最大收益（或等效地说，最小成本）的策略？

图1中假定了用户多次处于需要进行选择的场景中，每一次进行决策都会达成一项结果，而这个结果会关联相应的反馈。在上下班这个例子中，假定他每天都需要上下班，而且他每次上下班都必须进行线路的选择，产出的结果是这次上下班中所有因素的结合体，反馈就是从这些因素中构建出来的（陈运文 达观数据）。

这是个浅显的例子，在互联网产品研发时，有大量类似的场景需要做出各种正确的选择，例如：

1

着陆页优化（Landing-page optimization）

在用户点击去往的页面（着陆页），如何获得最大的转化率（常用计算方法为有购买行为或深度网页交互行为的用户数占网站访问总用户数的比率）。决策要考虑到着陆页的形式和内容（要从可能已有的3或4个备选方案中做出选择），希望能够从候选集合中选出最好的着陆页，以能够吸引来访的用户，并让深度交互或者购买行为的概率最大化。

2

广告创意优化（Ad creative optimization）

在线广告提出了许多适合机器学习技术应用的挑战，其中之一就是如何选择广告的形式和内容。当我们决定将要进行广告展示，以及确定了广告的价格后，在这个广告位上选择放置什么广告呢？我们需要对大量的决策进行测试，选出正确的广告创意组合。

NO.2

什么是A/B测试

经常遇到的问题是，我们应该怎么评估各不相同的决策，以及应该采用哪些策略来测试我们的产出？ A/B测试（A/B testing）就是其中之一的方法。A/B测试近年来很受欢迎，但大部分产品经理也许会简单地认为它只不过是一种包含两个组的实验，其实背后有更为复杂的数学统计理论知识。

具体细节

当进行A/B测试时，通常会采用两个（或多个）组：A组和B组。第一个组是对照组，第二个组会改变其中一些因素。就以着陆页优化为例，A组会展示现有的着陆页，B组会展示一个内容或者内容作了某些修改的新着陆页。A/B测试的目的就是尝试了解新的布局是否在统计上显著地改变了转化率。

特别值得注意的是，将用户分配到对应的组需要经过深思熟虑。对于A/B测试，我们可以高效地进行随机分组。当用户数量较大时，各组间用户行为可以假设是相同的（即组间没有偏差）。但是，这里有三个非常重要的关键点，是大家有必要进一步理解其数学理论原理的原因：

1

问题1

怎样验证两个组的用户的行为是无偏差、完全相同的

2

问题2

当两个组的用户行为不完全相同时（例如分组不够随机或者组内用户数量较小时），该如何设计AB测试以实现期望的验证结果

3

问题3

当用户基础行为受其他因素影响发生整体变化了呢？例如季节、时间波动、热度等因素影响下，怎样更好的剔除干扰来评估结果

NO.3

AB测试的统计理论

假设我们已经构建了两组数目较大的用户组，这些用户组的区别仅在于他们到达的着陆页。我们现在希望能测试两组间的转化率在统计上是否存在明显差异。由于样本量大，我们可以采用双样本单尾z-检验（two-sample, one-tailed z-test）。另外，对于较小的样本集合，我们可以依赖于t-检验。

z检验（z-test）是在数据是正态分布和随机抽样的假设下运行的，目的是验证测试集（B组）是否与该对照集（A组）有显著不同，但是如何执行这个测试呢？

假设有来自A组和B组中的每一组的5,000个样本。我们需要一个数学公式来说明我们的零假设（null hypothesis）——两组群体的转化率没有显著的正差异，和备择假设（或称对立假设，alternative hypothesis）——不同人群间的转化率确实存在着正差异。

我们可将采样转化率视为一个正态分布的随机变量，也就是说，采样的转化率是在正态分布下对转化率的一个观测。要了解这一点，请考虑从同一组中提取多个样本进行实验将导致略有不同的转化率。每当对某组进行抽样时，可获得群体转化率的估计，对于A组和B组都是如此。为此我们提出一个新的正态随机变量，它是A和B组的随机变量的组合，是差值的分布。让我们用X来表示这个新的随机变量，定义为:

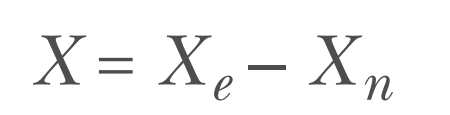
其中，Xe表示实验组的转化率的随机变量，Xn表示对照组的转化率的随机变量。现在我们可以写出零假设和备择假设。零假设可以表示为：

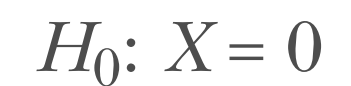
这表示实验组和对照组是相同的。两个随机变量Xe和Xn分布在相同的群体平均值周围，所以我们的新随机变量X应该分布在0左右。我们的备择假设可以表示如下:

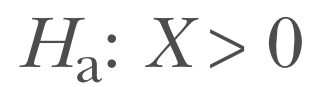
实验组的随机变量的期望值大于对照组的期望值；该群体的平均值较高。

我们可以在零假设的前提下，对X的分布执行单尾z检验，以确定是否有证据支持备择假设。为了达到这个目的，我们对X进行采样，计算标准分，并测试已知的显著性水平。

X的采样等效于运行两个实验，确定它们各自的转化率，并将对照组和实验组的转化率相减。按照标准分的定义，可以写作：

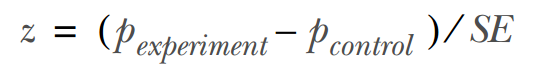
其中，P_experiment是实验组的转化率，P_control 是对照组的转化率，SE是转化率差值的标准差。

为确定标准误差，注意到转化过程是符合二项分布的，因此访问该网站可以被看作单次伯努利试验（single Bernoulli trial），而积极结果（完成转化）的可能性是未知的。

假设样本数量足够大，我们可以使用广泛采用的Wald方法（参考Lawrence D. Brown, T. Tony Cai, and Anirban DasGupta, “Confidence Intervals for a Binomial Proportion and Asymptotic Expansions,” The Annals of Statistics 30, no. 1 (2002): 160–201.）将该分布近似为正态分布。为了捕获特定转化率的不确定性，我们可以将标准误差（SE）写入实验组和对照组，其中p是转化的可能性，n是样本数量，具体如下：

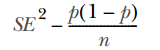
从二项分布（np（1-p））的方差得到分子，而分母表示当采用更多的样本时，转化率的误差会随之下降。请注意正面结果的概率等同于转化率，并且因为两个变量的标准误差可以通过相加来合并，得到如下结果：

通过替换，可获得如下的z检验公式，这是一个符合二项分布的Wald（或正态）区间的公式：

z的值越大，反对零假设的证据就越多。为了获得单尾测试的90％置信区间，我们的z值将需要大于1.28。这实际上这是指在零假设（A组和B组的人口平均值是相同的）的条件下，等于或大于这个转化率差值的偶然发生的概率小于10％。

换句话说，在对照组和实验组的转化率来自具有相同平均值的分布的假设前提下，如果运行相同的实验100次，只会有10次具有这样的极端值。我们可以通过95％的置信区间，更严格的边界和更多的证据来反对零假设，这时需要将z值增加到1.65。

研究影响z大小的因素会带来很多有用的帮助。很显然，如果在一个给定的时间点从一个实验集和一个对照集中提取两个转化率，转化率的差值越大将导致z分数越大。因此就有了更多的证据表明两个集合分别来自不同的人群，而且这些人群带有不同的均值。然而样品的数量也很重要，如你所见，大量样本将导致总体较小的标准误差。这表明运行实验的时间越长，转化率的估算越准确。

NO.4

评估效果的代码实现

设想你在负责大型零售网站，设计团队刚刚修改了着陆页。每周有约20,000用户，并可以量化用户的转化率：即购买产品的百分比。设计团队向你保证新网站将带来更多的客户。但你不太确定，希望运行A / B测试来看看效果是否真的会提高。

用户在第一次访问网站时被随机分配到A组或B组，并在实验期间始终保留在该组中，实验结束时评估两组用户的平均转化率。统计结果是，新着陆页的平均转化率是0.002，而原先的着陆页的平均转化率是0.001。在着陆页永久更改为新设计之前，你需要知道这一增长是否足够明确。下面这段代码帮你回答这个问题。

这段代码获取实验中z的值，在上述参数条件下z值为1.827，超过了92％置信区间，但不在95％的区间内。可以说，从控制分布中抽取数据的概率小于0.08。因此在该区间内数据提升是显著的。我们应该否定零假设，接受备择假设，即组之间有差异，第二组具有较高的转化率。如果我们控制了用户组的所有其他方面，就意味着网站的新设计产生了积极的效果。

你应该能够从代码中看到转化率分布的标准误差对返回的z值有直接影响。 对给定的常数值p_experiment和p_control，两个组的SE越高，z的数值越小，结果就越不显著。还注意到由于SE的定义，z的数值与样本的数量具有直接关系，对于给定的转换概率也同样如此。图2展示了这种关系。

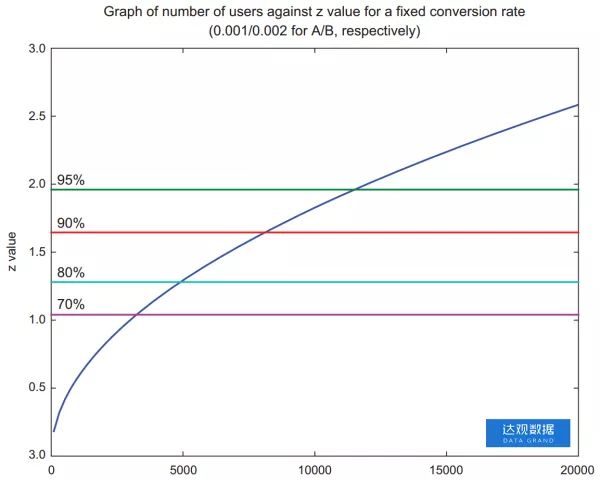
图2

图2 展示了A / B组的固定转化率，以及A / B组中的用户数量和z值之间的关系。 假设转化率不会随着我们收集更多数据而改变，我们需要每个组中大约3,000个用户达到70％的置信区间。 要达到80%的置信区间时需要每组约5000个用户，达到90%时需要 7500个用户，达到95%时需要12000个用户。

图2中可见对于两个组的给定转化率，测试组中的用户越多，备择假设的证据就越充分。直观上来看这很容易理解：当收集的数据越多，我们对结果越自信！我们也可以绘制一张类似的图，保持用户数量不变，改变组之间的差异。但必须注意，对正在关注的应用，不应该期望效果的大幅度变化。

 

NO.5

A/B测试方法的副作用和处理办法

对于非常小的效果变化，往往都需要创建相当大的对照组和测试组来实现AB测试，这个的代价往往是很大的。设想下在零售商场中，每天观察到的用户数量，往往需要很久的时间才能得出明显的结论。在实际业务应用中，会遇到的问题是：当你运行测试时整体运行的效果是受到很大影响的，因为必须有一半的用户处于效果不佳的实验组，或者有一半的用户处于效果不佳的对照组，而且你必须等待测试完成才能停止这种局面。

这是被称为探索利用难题（explore-exploit conundrum）的一个经典问题。我们需要运行次优方法，以探索空间，并找到效果更好的解决方案，而一旦找到了更好的解决方案，我们还需要尽快利用它们来实现效果提升。能否可以更快地利用新的解决方案，而不必等待测试完全完成呢？答案是肯定的。下面简单介绍下多臂赌博机（multi-armed bandit，MAB）的概念。

1

多臂赌博机的定义

多臂赌博机（multi-armed bandit，MAB）的名字来源于著名的赌博游戏角子赌博机（one-armed bandit）。对那些从没去过赌场的人，我们来做下解释：角子机（又称老虎机）是一个需要你拉杠杆（或摇臂）的赌博机器，根据机器展示的数值，你可能会得到一笔奖励，也可能（更大几率）得不到任何东西。和你想的一样，这些机器的设置都对庄家有利，所以能获的奖励的几率是非常非常小的。

多臂赌博机（理论上的）扩展了这种形式，想象你面对的是一堆角子赌博机，每个赌博机都被分配按照一个独立的概率进行奖励。作为一个玩家，你不知道在这些机器后的获奖概率，你唯一可以找到获奖概率的方法是进行游戏。你的任务是通过玩这些机器，最大限度地提高所获的奖励。那么你应该使用什么策略呢？

2

多臂赌博机策略

为了更严格地定义问题，我们通过数学形式化来表达，假设现在有k个赌博机，可观察到的每台的获奖概率等于p_k。假设一次只能拉动一个摇臂，并且赌博机只会按照它关联的概率机型奖励。这是一个设置了限定局数的有限次的游戏。在游戏期间任意时间点时，水平线H被定义为允许的剩余游戏的数量。

对所有机器用户会尝试最大化的获奖回报。在游戏中的任一时间点，我们都可以通过使用称为遗憾值（regret）来度量用户的表现。遗憾值的意思是，假设用户能在每一步选择最优的赌博机，得到的奖励和目前获得的实际奖励的差值。遗憾值的数学定义为:

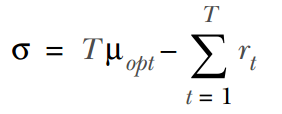
其中T表示我们到目前为止进行过的步数，r_t表示在第t步获得的奖励，u_opt表示每一局从最优赌博机返回来的期望奖励。遗憾值的数值越低，策略越优。但因为这个度量值会受到偶然性的影响（奖励可能会被从最优赌博机选择中获得的期望奖励更高），我们可以选择使用遗憾值的期望值代替,定义为:

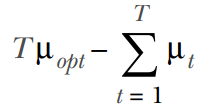
其中μ_t是在第t步从赌博机中获得的平均奖励（不可观测的）。因为第二项是来自所选策略的期望奖励，所以它将小于或等于来自最优策略（每一步都选择最优的赌博机）的期望奖励。

3

Epsilon优先方法

Epsilon优先（Epsilon first）是MAB策略中最简单的一种方式，它被认为和事先执行A/B测试方法具有同等意义。给定ε，执行探索空间操作的次数为(1 – ε) × N，其中N是游戏中总共的局数，剩余的次数都是执行后续探索的局数。

update_best_bandit算法会持续统计记录每一个赌博机的奖励收入和游戏局数。变best_bandit会在每一局结束进行更新，记录当前具有最高获奖概率的赌博机的编号，流程如下：

4

Epsilon贪婪

Epsilon贪婪（epsilon-greedy）策略中，ε表示我们进行探索空间的概率，和进行利用已知最优摇臂的事件互斥

该方法的特点：不需要等到探索阶段完成，才能开始利用有关赌博机的奖励表现的知识。但要小心，该算法不会考虑效果数据的统计意义。因此可能发生这样的情况：个别赌博机的奖励峰值导致后续的所有局游戏都错误地选择了这个赌博机（陈运文 达观数据）。

5

Epsilon递减

Epsilon递减（epsilon-decreasing）策略在实验开始阶段，会有一个很高的ε值，所以探索空间的可能性很高。ε值会随着水平线H上升而不断递减，致使利用似然知识的可能性更高。

需要注意这里有几种方法去来选择一个最优的速率来更新ε值，具体取决于赌博机的数量，以及他们各自进行奖励的权重。

6

贝叶斯赌博机

与A / B测试类似，贝叶斯赌博机（Bayesian bandits）假设每个赌博机的获奖概率被建模为获奖概率的分布。当我们开始实验时，每个赌博机都有一个通用的先验概率（任意赌博机的奖励比率初始都是同等的）。

在某一个赌博机上进行的局数越多，我们对它的奖励信息就了解越多，所以基于可能的奖励概率更新其获奖概率分布。当需要选择玩哪一个赌博机的时候，从获奖概率分布中采样，并选择对应样本中具有最高奖励比率的赌博机。图3提供了在给定时间内对三个赌博机所含信息的图形化表示。

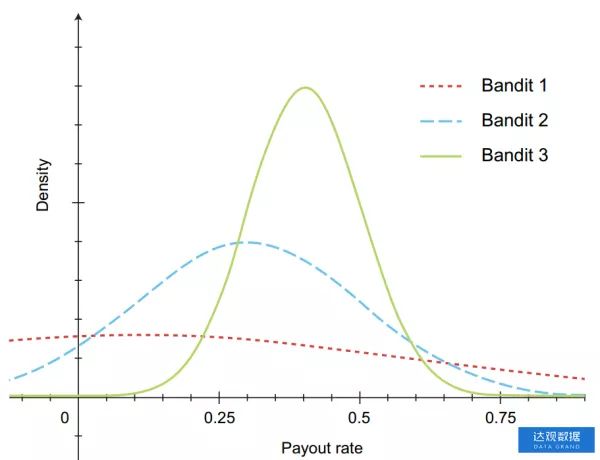
图3

使用贝叶斯赌博机策略对三个赌博机的获奖概率信息进行建模。第1、2和3个赌博机的平均获奖率分别为0.1、0.3和0.4。 第1个赌博机具有较低的平均值而且方差也比较大，第2个赌博机具有较高的平均值和较小的方差，第3个赌博机具有更高的平均值和更小的方差。

可以看到关于赌博机的获奖概率分布的信息被编码为三个分布。每个分布具有递增的平均值和递减的方差。因此，我们不太确定奖励期望值为0.1的真实奖励率，最可靠的是奖励期望值为0.4的赌博机。因为赌博机的选择是通过对分布进行抽样来进行的，所以分布期望值是0.1的赌博机的摇臂也可能被拉动。这个事件会发生在第2个赌博机和第3个赌博机的采样样本奖励值异常小，而且第1个赌博机的采样样本异常大时，相应代码如下（陈运文 达观数据）：

NO.6

总结

A/B测试和贝叶斯赌博机的各自的优点和局限是：两者有各自适用的场景，也验证的变量数量也各不相同，具体如下表。

此外，两个方法的收敛速度也很不一样。在A/B测试中是指获得统计意义，在贝叶斯赌博机中是指累积遗憾值不再增加。以本章最开始的网站优化为例，首先请注意，任何行为的改变可能是微小的（<0.01），而我们已经知道贝叶斯赌博机相比大的改变提升，需要更多的收敛时间。如果加了多种选择，在同一个实验中测试多种登陆页面，将更加会影响收敛速度。假如用户变化导致的底层分布变的比模型收敛更快呢？比如，季节趋势，销售或者其他因素可能会影响。

显然，收集的数据越多，对效果的潜在变化的把握度就越高。当2个组划分本身就存在统计差异时，通过多臂赌博机而不是A/B测试的方法可以从概率上修正我们选择的分布。本文还重点介绍了z检验（z-test）的数学知识，因为其构成了A/B测试的统计理论基础。

3 LDA-math-MCMC 和 Gibbs Sampling(2)
3.2 Markov Chain Monte Carlo

对于给定的概率分布p(x)p(x)。如何能做到这一点呢？我们主要使用如下的定理。
继续阅读 →

正态分布的前世今生 pdf 版

正态分布的前世今生 pdf 版(12pt 大字体版本)

评论欢迎发到 rickjin@新浪微博

 

(八)大道至简,大美天成

To see a world in a grain of sand
And a heaven in a wild flower,
Hold infinity in the palm of your hand
And eternity in an hour.

X¯=X1+X2+⋯+XnnX¯=X1+X2+⋯+Xnn

算术平均， 极其简单而朴素的一个式子，被人们使用了千百年，而在其身后隐藏着一个美丽的世界，而正态分布正是掌管这个美丽世界的女神。 正态分布的发现与应用的最初历史，就是数学家们孜孜不倦的从概率论和统计学角度对算术平均不断深入研究的历史。 中心极限定理在1773年棣莫弗的偶然邂逅的时候，它只是一粒普通的沙子， 两百多年来吸引了众多的数学家，这个浑金璞玉的定理不断的被概率学家们精雕细琢，逐渐的发展成为现代概率论的璀璨明珠。 而在统计学的误差分析之中，高斯窥视了造物主对算术平均的厚爱，也发现了正态分布的美丽身影。殊途同归，那是偶然中的必然。 一沙一世界，一花一天国, 算术平均或许只是一粒沙子， 正态分布或许只是一朵花，它们却包含了一个广阔而美丽的世界，几百年来以无穷的魅力吸引着科学家和数学家们。

高尔顿他对正态分布非常的推崇与赞美,1886 年他在人类学研究所的就职演讲中说过一段著名的话： ”我几乎不曾见过像误差呈正态分布这么美妙而激发人们无穷想象的宇宙秩序。 如果古希腊人知道这条曲线，想必会给予人格化乃至神格化。它以一种宁静无形的方式在最野性的混乱中实施严厉的统治。 暴民越多，无政府状态越显现， 它就统治得越完美。他是无理性世界中的最高法律。当我们从混沌中抽取大量的样本，并按大小加以排列整理时， 那么总是有一个始料不及的美妙规律潜伏在其中。“

概率学家 Kac 在他的自述传记《机遇之谜》中描述他与正态分布的渊源：“我接触到正态分布之后马上被他深深的吸引， 我感到难以相信，这个来自经验直方图和赌博游戏的规律，居然会成为我们日常生活数学的一部分。” 另一位概率学家 Loeve 说：“如果我们要抽取 Levy 的概率中心思想，那我们可以这样说， 自从 1919 年以后，Levy 研究的主题曲就是正态分布，他一而再再而三的以他为出发点，并且坚决的又回到她...... 他是带着随机时钟沿着随机过程的样本路径作旅行的人。” 美国国家标准局的顾问 W.J.Youden 用如下一段排列为正态曲线形状的文字给予正态分布极高的评价，意思是说： 误差的正态分布规律在人类的经验中具有“鹤立鸡群”的地位， 它在物理、社会科学、、医学、农业、工程等诸多领域都充当了研究的指南， 在实验和观测数据的解读中是不可或缺的工具。

几乎所有的人都或多或少的接触数学，虽然各自的目的不同，对数学的感觉也不同。 工程师、科学家们使用数学是因为他简洁而实用， 数学家们研究数学是因为它的美丽动人。像正态分布这样，既吸引着无数的工程师、科学家， 在实践中被如此广泛的应用，又令众多的数学家为之魂牵梦绕的数学存在，在数学的世界里也并不多见。 我在读研究生的时候，经常逛北大未名BBS 的数学板，有一个叫 ukim 的著名 ID 在精华区里面留下了一个介绍数学家八卦的系列《Heroes in My Heart》，写得非常的精彩， 这些故事在喜欢数学的人群中也流传广泛。 最后一个八卦是关于菲尔兹奖得主法国数学家 R.Thom的，它曾经令无数人感动， 我也借用来作为我对正态分布的八卦的结语：

在一次采访当中，作为数学家的 Thom同两位古人类学家讨论问题。 谈到远古的人们为什么要保存火种时，一个人类学家说，因为保存 火种可以取暖御寒；另外一个人类学家说，因为保存火种可以烧出 鲜美的肉食。而 Thom 说，因为夜幕来临之际，火光摇曳妩媚，灿 烂多姿，是最美最美的......

（九)推荐阅读

在终极的分析中，一切知识都是历史
在抽象的意义下，一切科学都是数学
在理性的基础上，所有的判断都是统计学
-- C.R.Rao

本人并非统计学专业人士，只是凭一点兴趣做一点知识的传播，对统计学历史知识的介绍，专业性和系统性都不是我的目的。 我更在乎的是趣味性，因为没有趣味就不会有传播。如果读完这段历史会让你觉得正态分布更加亲切，不再那么遥不可及， 那我的目的达到了。如果正态分布是一滴水，我愿大家都能看到它折射出的七彩虹。

本文所使用的大多是二手资料，有些历史细节并没有经过严格的考证，对于历史资料一定程度上按照个人喜好做了取舍， 本文主要基于如下的资料写成，对于历史细节感兴趣，不希望被我误导的，推荐阅读。

• 陈希孺, 数理统计学简史
• 蔡聰明,誤差論與最小平方法,数学传播
• 吴江霞,正态分布进入统计学的历史演化
• E.T. Jaynes, Probability Theory, The Logic of Science (概率论沉思录)
• Saul Stahl, The Evolution of the Normal Distribution
• Kiseon Kim, Why Gaussianity
• Stigler, Stephen M. The History of Statistics: The Measurement of Uncertainty before 1900.
• L.Le Cam, The Central Limit Theorem Around 1935
• Hans Fischer, A History of the Central Limit Theorem: From Classical to Modern Probability Theory

(七)正态魅影

Everyone believes in it: experimentalists believing that it is a
mathematical theorem, mathematicians believing that it is an empirical fact.
---- Henri Poincare

f(x)=12π−−√σe−(x−μ)22σ2f(x)=12πσe−(x−μ)22σ2独立，而正态分布是唯一满足这一性质的概率分布

（六)开疆扩土，正态分布的进一步发展

2.进军近代统计学

花开两朵，各表一枝。上面说了围绕正态分布在概率论中的发展，现在来看看正态分布在数理统计学中发展的故事。 这个故事的领衔主演是 Adolphe Quetelet和高尔顿(Galton)。

由于高斯的工作，正态分布在误差分析迅速确定了自己的定位，有了这么好的工具，我们可能拍脑袋就认为，正态分布很快 就被人们用来分析其它的数据，然而事实却出乎我们的意料，正态分布进入社会领域和自然科学领域，可是经过一番周折的。

首先我要告诉大家一个事实：误差分析和统计学是两个风马牛不相及的两个学科。 当然这个事实存在的时间是19世纪初之前。统计学的产生最初是与“编制国情报告”有关，主要服务于政府部门。 统计学面对的是统计数据，是对多个不同对象的测量；而误差分析研究的是观测数据， 是对同一个对象的多次测量。因此观测数据和 统计数据在当时被认为两种不同行为获取得到的数据，适用于观测数据的规律未必适用于统计数据。 19世纪的统计数据分析处于一个很落后的状态，和概率论没有多少结合。 而概率论的产生主要和赌博相关，发展过程中与误差分析紧密联系， 而与当时的统计学交集非常小。将统计学与概率论真正结合起来推动数理统计学发展的便是我们的统计学巨星Quetelet。

Quetelet这名字或许不如其它数学家那么响亮，估计很多人不熟悉，所以有必要介绍一下。 Quetelet是比利时人，数学博士毕业，年轻的时候曾追谁拉普拉斯学习过概率论。 此人学识渊博，涉猎广泛，脑门上的桂冠包括统计学家、数学家、天文学家、社会学家、 国际统计会议之父、近代统计学之父、数理统计学派创始人。 Quetelet 的最大的贡献就是将法国的古典概率引入统计学，用纯数学的方法对社会现象进行研究。

1831年，Quetelet参与主持新建比利时统计总局的工作。他开始从事有关人口问题的统计学研究。 在这种研究中，Quetelet发现,以往被人们认为杂乱无章的、偶然性占统治地位的社会现象， 如同自然现象一样也具有一定的规律性。 Quetelet 搜集了大量关于人体生理测量的数据，如体重、身高与胸围等，并使用概率统计方法来 对数据进行数据分析。但是当时的统计分析方法遭到了社会学家的质疑， 社会学家们的反对意见主要在于：社会问题 与科学实验不同，其数据一般由观察得到，无法控制且经常不了解其异质因素，这样数据 的同质性连带其分析结果往往就有了问题，于是社会统计工作者就面临一个如何判 断数据同质性的问题。Quetelet大胆地提出：

把一批数据是否能很好地拟合正态分布，作为判断该批数据同质的依据。

Quetelet提出了一个使用正态曲线拟合数据的方法，并广泛的使用正态分布去拟合各种类型的数据。 由此， Quetelet为正态分布的应用拓展了广阔的舞台。 正态分布如同一把屠龙刀，在Quetelet 的带领下，学者们挥舞着这把宝刀在各个领域披荆斩棘， 攻陷了人口、领土、政治、农业、工业、商业、道德等社会领域， 并进一步攻占天文学、数学、物理学、生物学、社会统计学及气象学等自然科学领域。

正态分布的下一个推动力来自生物学家高尔顿，当正态分布与生物学联姻时，近代统计学迎来了一次大发展。 高尔顿是生物统计学派的奠基人，他的表哥达尔文的巨著《物种起源》问世以后，触动他用统计方法研究遗传进化问题。 受Quetelet的启发，他对正态分布怀有浓厚的兴趣，开始使用正态分布去拟合人的身高、胸围、以至考试成绩等各类数据， 发现正态分布拟合得非常好。他因此相信正态曲线是适用于无数情况的一般法则。

然而，对高尔顿而言，这个无处不在的正态性给他带来一些困惑。他考察了亲子两代的身高数据， 发现遵从同一的正态分布，遗传作为一个显著因素是如何发挥作用的？1877年， 高尔顿设计了一个 叫高尔顿钉板(quincunx, 或者Galton board)的装置，模拟正态分布的性质用于解释遗传现象。

如下图中每一点表示钉在板上的一颗钉子，它们彼此的距离均相等。 当小圆球向下降落过程中，碰到钉子后皆以 1212分布。所以正态 分布在19世纪是武则天，进入二十世纪就学了慈禧太后，垂帘听政了。 或者，换个角度说，一个好汉三个帮，正态分布如果是孤家寡人恐怕也难以雄霸天下， 有了统计学三大分布作为开国先锋为它开疆拓土，正态分布真正成为傲世群雄的君王。

20世纪初，统计学这三大剑客成为了现代数理统计学的奠基人。以哥塞特为先驱，费歇尔为主将， 掀起了小样本理论的革命，事实上提升了正态分布在统计学中的地位。 在数理统计学中，除了以正态分布为基础的小样本理论获得了空前的胜利，其它分布上都没有成功的案例， 这不能不让人对正态分布刮目相看。在随后的发展中，相关回归分析、多元分析、方差分析、因子分析、 布朗运动、高斯过程等等诸多统计分析方法陆续登上了历史舞台， 而这些和正态分布密切相关的方法，成为推动现代统计学飞速发展的一个强大动力。

	<footer class="entry-meta">本条目发布于<a href="http://www.52nlp.cn/%e6%ad%a3%e6%80%81%e5%88%86%e5%b8%83%e7%9a%84%e5%89%8d%e4%b8%96%e4%bb%8a%e7%94%9f%e5%85%ad" title="20:10" rel="bookmark"><time class="entry-date" datetime="2012-10-25T20:10:46+00:00">2012年10月25号</time></a>。属于<a href="http://www.52nlp.cn/category/%e7%bb%9f%e8%ae%a1%e5%ad%a6" rel="category tag">统计学</a>、<a href="http://www.52nlp.cn/category/nlp" rel="category tag">自然语言处理</a>分类，被贴了 <a href="http://www.52nlp.cn/tag/%e6%ad%a3%e6%80%81%e5%88%86%e5%b8%83" rel="tag">正态分布</a>、<a href="http://www.52nlp.cn/tag/%e6%ad%a3%e6%80%81%e5%88%86%e5%b8%83%e7%9a%84%e5%89%8d%e4%b8%96%e4%bb%8a%e7%94%9f" rel="tag">正态分布的前世今生</a> 标签。<span class="by-author">作者是<span class="author vcard"><a class="url fn n" href="http://www.52nlp.cn/author/rickjin" title="查看所有由rickjin发布的文章" rel="author">rickjin</a></span>。</span>								</footer><!-- .entry-meta -->
</article><!-- #post --><article id="post-4770" class="post-4770 post type-post status-publish format-standard hentry category-538 tag-539 tag-543 tag-1244"><header class="entry-header"><h1 class="entry-title"><a href="http://www.52nlp.cn/%e6%ad%a3%e6%80%81%e5%88%86%e5%b8%83%e7%9a%84%e5%89%8d%e4%b8%96%e4%bb%8a%e7%94%9f%e4%ba%94" rel="bookmark">正态分布的前世今生(五)</a></h1><div class="comments-link"><a href="http://www.52nlp.cn/%e6%ad%a3%e6%80%81%e5%88%86%e5%b8%83%e7%9a%84%e5%89%8d%e4%b8%96%e4%bb%8a%e7%94%9f%e4%ba%94#comments">2条回复</a>				</div><!-- .comments-link --></header><!-- .entry-header --><div class="entry-content"><div class="code-block code-block-1" style="margin: 8px auto; text-align: center; clear: both;">

（六) 开疆扩土，正态分布的进一步发展

19世纪初，随着拉普拉斯中心极限定理的建立与高斯正态误差理论的问世，正态分布开始崭露头角， 逐步在近代概率论和数理统计学中大放异彩。在概率论中，由于拉普拉斯的推动，中心极限定理发展 成为现代概率论的一块基石。而在数理统计学中，在高斯的大力提倡之下，正态分布开始逐步畅行于天下。

1. 论剑中心极限定理

先来说说正态分布在概率论中的地位，这个主要是由于中心极限定理的影响。 1776 年，拉普拉斯开始考虑一个天文学中的彗星轨道的倾角的计算问题，最终的问题涉及 独立随机变量求和的概率计算，也就是计算如下的概率值

Sn=X1+X2+⋯+XnSn=X1+X2+⋯+Xn

理科专业的本科生学习《概率论与数理统计》这门课程的时候， 除了学习棣莫弗-拉普拉斯中心极限定理，通常还学习如下中心极限定理的一般形式：

[Lindeberg-Levy 中心极限定理] 设X