链接：https://arxiv.org/pdf/1705.02426.pdf
本文的主要创新点就是把类比推理应用到 KG embedding 中，通过对模型的 score function 添加某些约束来捕获 KG 中类比结构的信息，进而优化 KG 中实体和关系的 embedding 表示，并在 FB15K 和 WN18 数据集上达到 state-of -the-art 性能。
Analogical Structure
什么是类比结构？以 word embedding中最著名的一句话为例，man is to king as woman is to queen，用 abcd 分别表示 man, king, woman, queen 四个实体，用 r 和 r' 表示 crown 和 male->female 关系，这就可以得到四个三元组
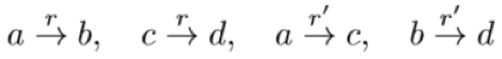
可视化一下，就可以得到一个平行四边形结构，捕获这个结构的信息也就是本文的 motivation，且更复杂的类比结构的基本组成单元就是这个平行四边形结构。
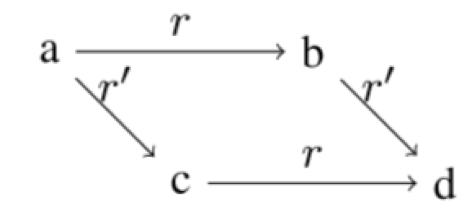
对于线性映射来说，一个理想的特性，就是所有有相同起点和终点的有向图，都形成了所谓的compositional equivalence，在上图中就是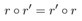
，且若关系集合R中任意两个关系都满足compositionalequivalence，则称R是一个commutingfamily。
Method
本文将关系 r 视为线性映射，即给定三元组 (s,r,o)，作者希望对于所有有效的三元组，都能满足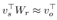
，满足的程度就用一个 score function 表示，模型的目标就是学到恰当的 v 和 W，来让这个 score function 给有效的三元组高分，无效的三元组低分。为什么用线性映射而不用transE那样的加法映射呢？作者的看法是，用矩阵定义的线性映射表达能力比用向量定义的加法映射更强。
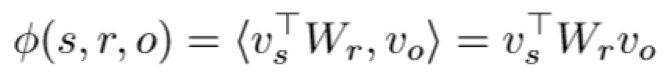
为了捕获 KG 中类比结构的信息，本文在objective function上加入了 Normal Matrix 和 compositional equivalence 的约束，而后者就是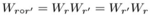
，即在线性映射上的具体实现，最后得到的 objective function 就是
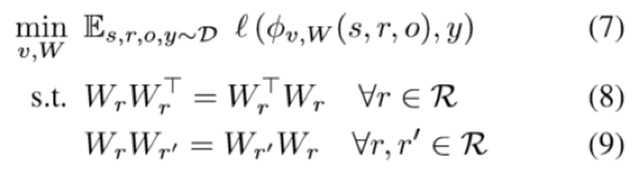
Why Normal Matrix
引理1，对于任意实正规矩阵 A，存在一个实正交矩阵 Q 和分块对角矩阵 B，满足 A=QBQT，其中 B 的每个对角块要么是个实数，要么是个2维实矩阵，x 和 y都是实数。这个引理表明任意一个实正规矩阵都可以分块对角化。
引理2，若一系列实正规矩阵组成了一个 commuting family，那么它们可以用同一个 Q 分块对角化。这个引理表明，若一个稠密关系矩阵集合｛Wr｝相互可交换，那么就可以同时被分块对角化成一个稀疏矩阵集合｛Br｝。
结合以上两个性质，可以对 score function 进行推导，过程如下
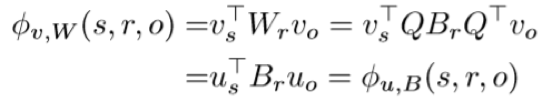
即对于任意目标函数7的解 (v*,W*) ，都有对应的 (u*,B*) 满足
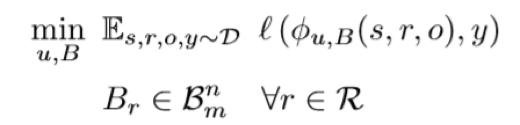
目标函数简化成了这个样子，其中 B表示对角线上有n个实数的m阶对角方阵。
Unified View of Representative Methods
作者也证明了本文模型是 unified method，以 DistMult为例，它的 score func 如
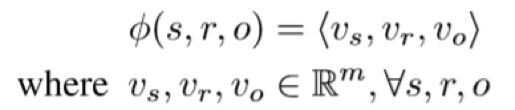
实际上这就是 n=m 的ANALOGY版本，其中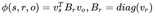
。
Experiments
实验用的数据集是FB15K和WN18，作者用了19个baseline做对比，metrics用的也是常用的MRR和Hits@k。由下表可以知道FB15K的关系数非常多，因此对其建模也更难，KG中包含的类比结构也更多，而在这个数据集上，ANALOGY的表现超过了所有baseline模型，这证明了捕获类比结构信息的作用。
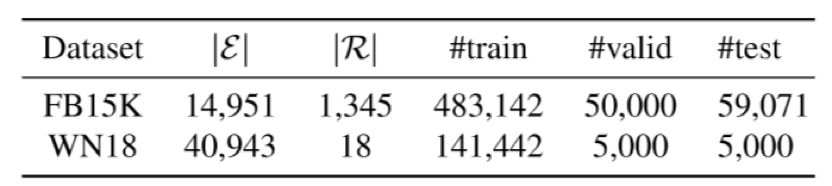
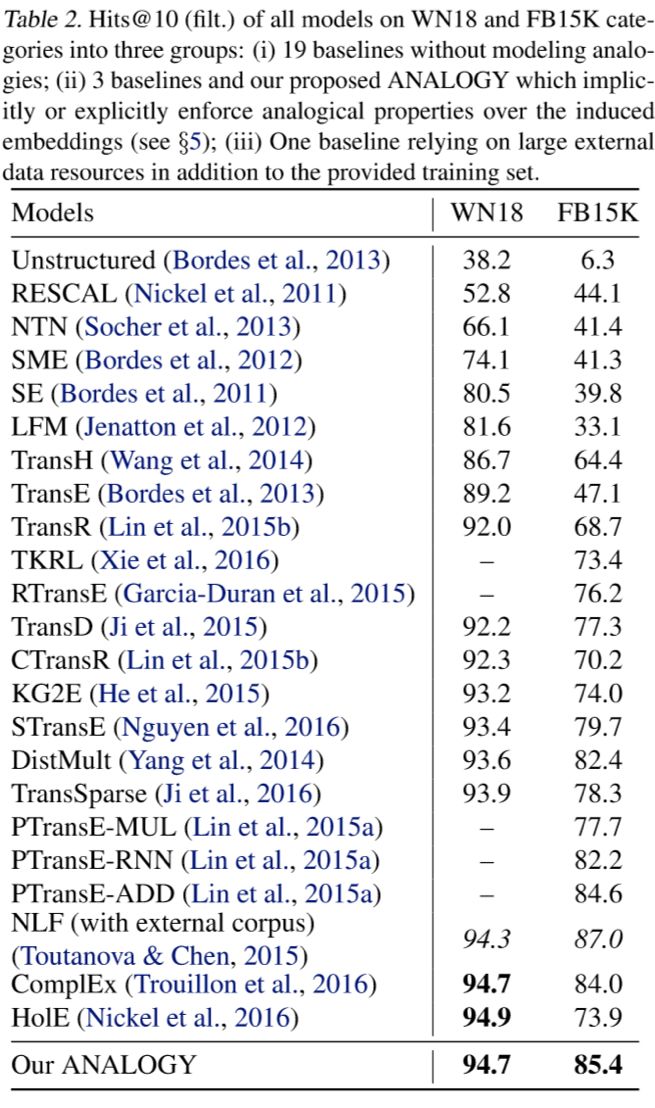
而下图则表明在所有指标上，ANALOGY的表现都超过了 DistMult,ComplEx和HolE，且这三个是ANALOGY的特例。
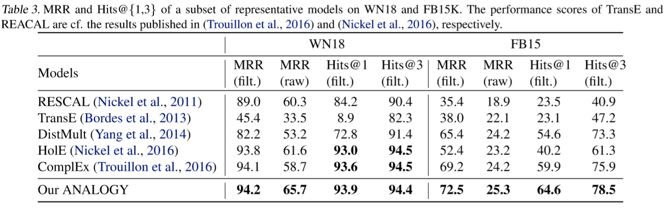
论文笔记整理：汪寒，浙江大学硕士，研究方向为知识图谱，自然语言处理。
OpenKG.CN
中文开放知识图谱（简称OpenKG.CN）旨在促进中文知识图谱数据的开放与互联，促进知识图谱和语义技术的普及和广泛应用。
点击阅读原文，进入 OpenKG 博客。
