文章目录
- 1.概念
- 2.存储方式
- 2.1 链式存储(二叉树代码大部分是链式实现的)
- 2.2 顺序存储(基于数组)
- 3.二叉树的遍历
- 3.1 基于链表的二叉树实现代码
- 3.2 基于数组的二叉树实现代码
- 3.3 非递归法 二叉树遍历

1.概念
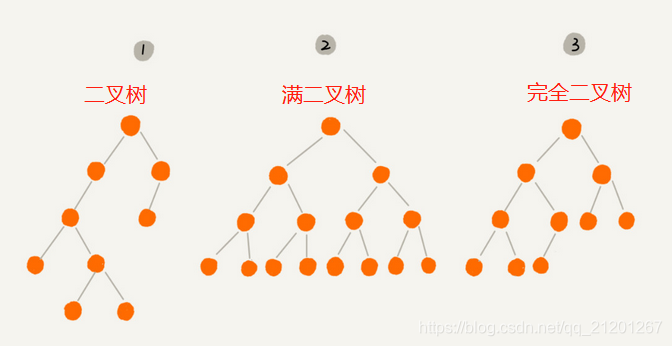
- 二叉树,每个节点最多有两个“叉”,也就是两个子节点,分别是左子节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点
- 满二又树,叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点。
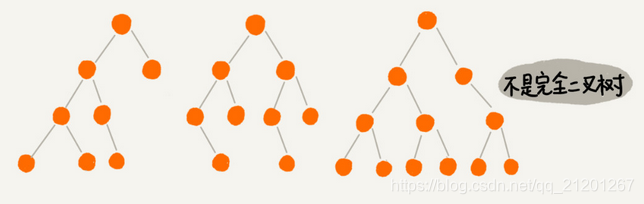
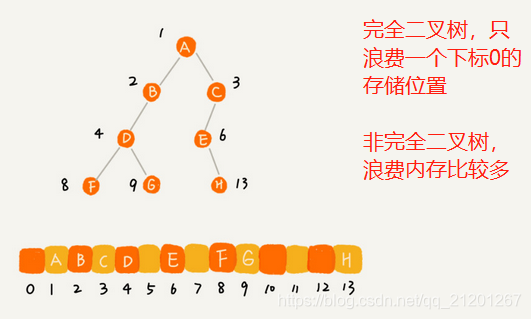
- 完全二叉树,叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大。
2.存储方式
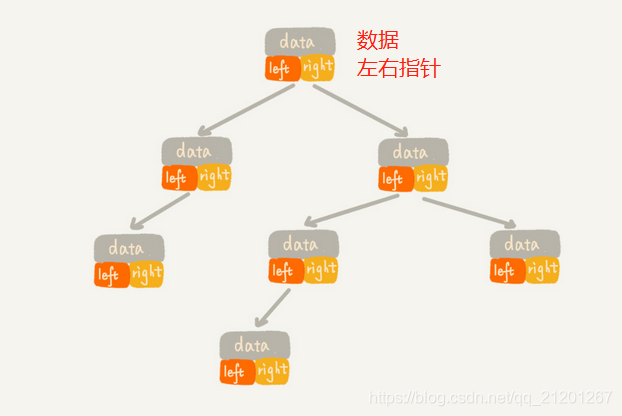
2.1 链式存储(二叉树代码大部分是链式实现的)
2.2 顺序存储(基于数组)
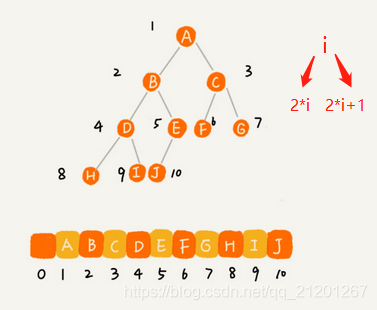
- 把根节点存储在下标 i = 1 的位置,那左子节点存储在下标 2 * i = 2 的位置,右子节点存储在 2 * i + 1 = 3 的位置。
- 以此类推,B节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置,右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。
堆排序中的堆就是完全二叉树。
3.二叉树的遍历
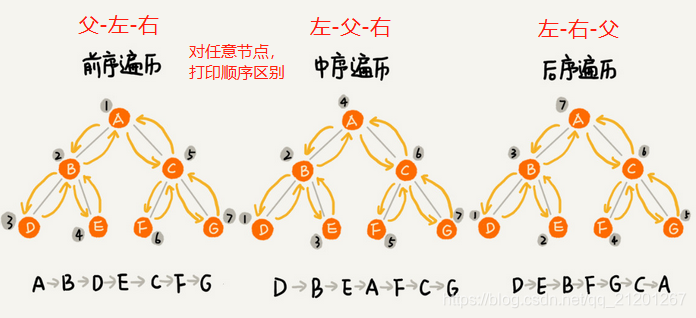
void preOrder(Node* root)
{if(root==NULL)return;print root; //打印root节点preOrder(root->1eft);preOrder(root->right);
}
void inorder(Node* root)
{if(root==NULL)return;inorder(root->1eft);print root; //打印root节点inorder(root->right);
}
void postorder(Node* root)
{if(root==NULL)return;postorder(root->1eft);postorder(root->right);print root; //打印root节点
}
void levelorder(Node* root) //按层从左至右打印
{if(root==NULL)return;queue<node*> nodeQueuenodequeue.push(root);while(!nodequeue.empty()) //建立节点队列,打印父节点,入队左右子节点,出队父节点{node* p = nodeQueue.front();cout << p->data << " ";if(p->left != NULL)nodeQueue.push(p->left);if(p->right != NULL)nodeQueue.push(p->right);nodeQueue.pop();}
}
每个节点最多会被访问 2 次, 所以遍历操作的时间复杂度, 跟节点的个数 n 成正比,二叉树遍历的时间复杂度是 O(n)
3.1 基于链表的二叉树实现代码
/*** @description: 二叉树,链表实现* @author: michael ming* @date: 2019/5/11 18:03* @modified by: */
#include <iostream>
#include <queue>
#include <stack>
using namespace std;
template <class T>
struct node
{T data;node<T> *left, *right;node<T>():left(NULL), right(NULL){}
};
template <class T>
class binary_tree
{
private:int nodelen;node<T> *root;
public:binary_tree():nodelen(0), root(NULL){}node<T>* getRoot()const{return root;}node<T>* insert(node<T> * nodep, size_t lv, size_t toplv, int data = 1){if(lv == 0)return NULL;else if(nodep == NULL && lv == toplv){root = new node<T>();nodep = root;}else{nodep = new node<T>();}nodep->data = data;nodelen++;node<T>* l = insert(nodep->left, lv-1, toplv, 2*data);if(l)nodep->left = l; //返回创建好的left节点l,跟父接上node<T>* r = insert(nodep->right, lv-1, toplv, 2*data+1);if(r)nodep->right = r; //返回创建好的right节点r,跟父接上return nodep;}void preOrderPrint(node<T> * nodep){if (nodep == NULL)return;cout << nodep->data << " ";preOrderPrint(nodep->left);preOrderPrint(nodep->right);}void inOrderPrint(node<T> * nodep){if (nodep == NULL)return;inOrderPrint(nodep->left);cout << nodep->data << " ";inOrderPrint(nodep->right);}void postOrderPrint(node<T> * nodep){if (nodep == NULL)return;postOrderPrint(nodep->left);postOrderPrint(nodep->right);cout << nodep->data << " ";}void levelOrderPrint(node<T> * nodep) //按层打印{if (nodep == NULL)return;queue<node<T>*> nodequeue;nodequeue.push(nodep);while(!nodequeue.empty()) //建立节点队列,打印父节点,入队左右子节点,出队父节点{node<T>* p = nodequeue.front();cout << p->data << " ";if(p->left != NULL)nodequeue.push(p->left);if(p->right != NULL)nodequeue.push(p->right);nodequeue.pop();}}void destory_tree(node<T> * nodep){if (nodep == NULL)return;destory_tree(nodep->left);destory_tree(nodep->right);delete nodep;}//-----------------求二叉树高度-----------------------int get_height(node<T>* nodep) //递归法, 求左右子树高度,较大的+1{if(nodep == NULL)return 0;int leftheight = get_height(nodep->left);int rightheight = get_height(nodep->right);return max(leftheight, rightheight) + 1;}int level_get_height(node<T>* nodep) //按层计算高度{if (nodep == NULL)return 0;queue<node<T>*> nodequeue;node<T>* p = NULL;nodequeue.push(nodep);int height = 0;while(!nodequeue.empty()) //建立节点队列,入队左右子节点,出队父节点{height++;int n = nodequeue.size();for(int i = 0; i < n; ++i){p = nodequeue.front();if(p->left != NULL)nodequeue.push(p->left);if(p->right != NULL)nodequeue.push(p->right);nodequeue.pop();}}return height;}int stack_get_height(node<T>* nodep) //用栈实现前序(或后序)遍历,最大栈长度即为树的高度{if (nodep == NULL)return 0;stack<node<T>*> nodestack;node<T> *temp = NULL;int height = 0;while(nodep != NULL || !nodestack.empty()){if(nodep != NULL){nodestack.push(nodep);nodep = nodep->left;//找到最底端左节点}else{nodep = nodestack.top();//最底端左节点的父节点nodepif(nodep->right != NULL && nodep->right != temp) //右边有节点,且没有进过栈nodep = nodep->right; //进入右节点,跳到上个if查其子树else //没有子节点,或者子节点进过栈{if(nodestack.size() > height)height = nodestack.size(); //更新最大高度temp = nodep; //记录弹栈的节点到tempnodestack.pop();nodep = NULL;}}}return height;}
};int main()
{binary_tree<int> btree;btree.insert(btree.getRoot(), 3, 3);btree.preOrderPrint(btree.getRoot());cout << endl << endl;btree.inOrderPrint(btree.getRoot());cout << endl << endl;btree.postOrderPrint(btree.getRoot());cout << endl << endl;btree.levelOrderPrint(btree.getRoot());cout << endl;cout << "height of tree: " << btree.get_height(btree.getRoot()) << endl;cout << "level height of tree: " << btree.level_get_height(btree.getRoot()) << endl;cout << "stack height of tree: " << btree.stack_get_height(btree.getRoot()) << endl;btree.destory_tree(btree.getRoot());return 0;
}
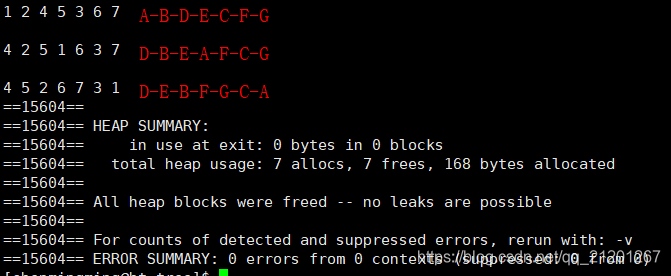

3.2 基于数组的二叉树实现代码
/*** @description: 二叉树,数组实现* @author: michael ming* @date: 2019/5/11 11:44* @modified by: */
#include <iostream>
using namespace std;
template <class T>
struct node
{T data;node<T>(){}
};
template <class T>
class binary_tree
{
private:int size;size_t tree_arrlen;node<T>* tree;
public:binary_tree(int len = 20):size(len),tree_arrlen(0){tree = new node<T> [size];}~binary_tree(){delete [] tree;}void insert(T &data){if(tree_arrlen < size)tree[++tree_arrlen].data = data;}void preOrderPrint(size_t index = 1){if(tree_arrlen < 1 || index > tree_arrlen)return;cout << tree[index].data << " ";preOrderPrint(index*2);preOrderPrint(index*2+1);}void inOrderPrint(size_t index = 1){if(tree_arrlen < 1 || index > tree_arrlen)return;inOrderPrint(index*2);cout << tree[index].data << " ";inOrderPrint(index*2+1);}void postOrderPrint(size_t index = 1){if(tree_arrlen < 1 || index > tree_arrlen)return;postOrderPrint(index*2);postOrderPrint(index*2+1);cout << tree[index].data << " ";}
};int main()
{binary_tree<int> btree;for(int i = 1; i < 8; ++i)btree.insert(i);btree.preOrderPrint();cout << endl;btree.inOrderPrint();cout << endl;btree.postOrderPrint();return 0;
}
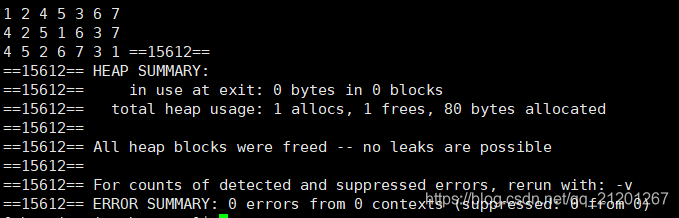
3.3 非递归法 二叉树遍历
- 前序(入栈root,访问stack.top(), 出栈,依次入栈右节点,左节点)
void stackPreOrder()
{stack<node<T>*> nodeStack;node<T> * nodep = root;if(nodep != NULL){nodeStack.push(nodep);while(!nodeStack.empty()){nodep = nodeStack.top();nodeStack.pop();cout << nodep->data << " ";if(nodep->right != NULL) //注意左右节点入栈顺序!!!nodeStack.push(nodep->right);if(nodep->left != NULL)nodeStack.push(nodep->left);}}
}
- 中序(入栈右、根、(左的右、左的根、…),左右节点为空,到达叶子节点,打印叶子节点,)
void stackInOrder()
{stack<node<T>*> nodeStack;node<T> *nodep = root;while(nodep != NULL){while(nodep != NULL)//入栈右、根{if(nodep->right)nodeStack.push(nodep->right);nodeStack.push(nodep);nodep = nodep->left;}nodep = nodeStack.top();//根节点nodeStack.pop();while(!nodeStack.empty() && nodep->right == NULL)//nodep为叶子节点{cout << nodep->data << " ";//打印叶子节点nodep = nodeStack.top();nodeStack.pop();}cout << nodep->data << " ";//左节点为空,右节点非空or最后一个节点if(!nodeStack.empty()){nodep = nodeStack.top();nodeStack.pop();}elsenodep = NULL;}
}
- 后序
void stackPostOrder()
{stack<node<T>*> nodeStack;node<T> *nodep = root, *temp = root;while(nodep != NULL){for(;nodep->left != NULL; nodep = nodep->left)nodeStack.push(nodep); //入栈一路上的左节点while(nodep->right == NULL || nodep->right == temp){cout << nodep->data << " ";//打印叶子节点temp = nodep;if(nodeStack.empty())return;nodep = nodeStack.top();//回到父节点nodeStack.pop();}nodeStack.push(nodep);nodep = nodep->right;//转到右子树}
}
完整代码
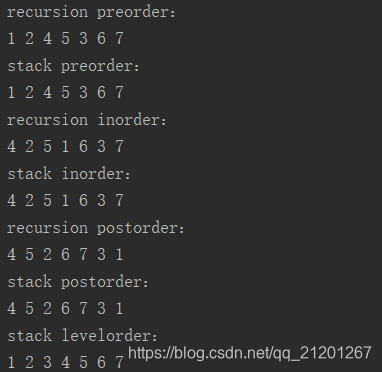








)



)


)



)