LeetCode 第 27 场双周赛（1125/1966，前57.2%）

文章目录

- 1. 比赛结果
- 2. 题目
- - 1. LeetCode 5408. 通过翻转子数组使两个数组相等 easy
  - 2. LeetCode 5409. 检查一个字符串是否包含所有长度为 K 的二进制子串 medium
  - 3. LeetCode 5410. 课程安排 IV medium （Floyd-Warshall）
  - 4. LeetCode 5411. 摘樱桃 II hard

1. 比赛结果

虽然只做出一题，还是记录一下吧。第一题送分题拿下，第二题没绕过弯，第三题超时，第四题没看。继续加油！

全国排名：1125 / 1966，57.2%；全球排名：4236 / 7924，53.5%

在这里插入图片描述

2. 题目

1. LeetCode 5408. 通过翻转子数组使两个数组相等 easy

题目链接
给你两个长度相同的整数数组 target 和 arr 。

每一步中，你可以选择 arr 的任意 非空子数组 并将它翻转。你可以执行此过程任意次。

如果你能让 arr 变得与 target 相同，返回 True；否则，返回 False 。

示例 1：
输入：target = [1,2,3,4], arr = [2,4,1,3]
输出：true
解释：你可以按照如下步骤使 arr 变成 target：
1- 翻转子数组 [2,4,1] ，arr 变成 [1,4,2,3]
2- 翻转子数组 [4,2] ，arr 变成 [1,2,4,3]
3- 翻转子数组 [4,3] ，arr 变成 [1,2,3,4]
上述方法并不是唯一的，还存在多种将 arr 变成 target 的方法。示例 2：
输入：target = [7], arr = [7]
输出：true
解释：arr 不需要做任何翻转已经与 target 相等。示例 3：
输入：target = [1,12], arr = [12,1]
输出：true示例 4：
输入：target = [3,7,9], arr = [3,7,11]
输出：false
解释：arr 没有数字 9 ，所以无论如何也无法变成 target 。示例 5：
输入：target = [1,1,1,1,1], arr = [1,1,1,1,1]
输出：true提示：
target.length == arr.length
1 <= target.length <= 1000
1 <= target[i] <= 1000
1 <= arr[i] <= 1000

解答：

翻转任意次，那就排序后，相等即可

class Solution {
public:bool canBeEqual(vector<int>& target, vector<int>& arr) {sort(target.begin(), target.end());sort(arr.begin(),arr.end());return target == arr;}
};

2. LeetCode 5409. 检查一个字符串是否包含所有长度为 K 的二进制子串 medium

题目链接
给你一个二进制字符串 s 和一个整数 k 。

如果所有长度为 k 的二进制字符串都是 s 的子串，请返回 True ，否则请返回 False 。

示例 1：
输入：s = "00110110", k = 2
输出：true
解释：长度为 2 的二进制串包括 "00"，"01"，"10" 和 "11"。
它们分别是 s 中下标为 0，1，3，2 开始的长度为 2 的子串。示例 2：
输入：s = "00110", k = 2
输出：true示例 3：
输入：s = "0110", k = 1
输出：true
解释：长度为 1 的二进制串包括 "0" 和 "1"，显然它们都是 s 的子串。示例 4：
输入：s = "0110", k = 2
输出：false
解释：长度为 2 的二进制串 "00" 没有出现在 s 中。示例 5：
输入：s = "0000000001011100", k = 4
输出：false提示：
1 <= s.length <= 5 * 10^5
s 中只含 0 和 1 。
1 <= k <= 20

解题：

大小为k的滑动窗口，把字符串取出来，转成int放入集合，看集合中数的种类是不是 2^k 个

class Solution {
public:bool hasAllCodes(string s, int k) {if(s.size() <= k)return false;int i, l = 0, r = 0, num;set<int> st;for( ; r < s.size(); ++r){if(r-l+1 == k)//长度为 k {num = 0;for(i = l; i <= r; ++i)//转成数字num = s[i]-'0' + (num<<1);st.insert(num);l++;}}return st.size()== (1<<k);}
};

968 ms 38.9 MB

stoi函数简化代码 http://www.cplusplus.com/reference/string/stoi/

将字符串从给定下标开始的字符子串，从base进制 转成 10 进制int
int stoi (const string&  str, size_t* idx = 0, int base = 10);
int stoi (const wstring& str, size_t* idx = 0, int base = 10);

class Solution {
public:bool hasAllCodes(string s, int k) {if(s.size() <= k)return false;int i, l = 0, r = 0;set<int> st;string str;for( ; r < s.size(); ++r){if(r-l+1 == k){str = s.substr(l,k);st.insert(stoi(str,0,2));l++;}}return st.size()== (1<<k);}
};

1392 ms 50.2 MB

3. LeetCode 5410. 课程安排 IV medium （Floyd-Warshall）

题目链接
你总共需要上 n 门课，课程编号依次为 0 到 n-1 。

有的课会有直接的先修课程，比如如果想上课程 0 ，你必须先上课程 1 ，那么会以 [1,0] 数对的形式给出先修课程数对。

给你课程总数 n 和一个直接先修课程数对列表 prerequisite 和一个查询对列表 queries 。

对于每个查询对 queries[i] ，请判断 queries[i][0] 是否是 queries[i][1] 的先修课程。

请返回一个布尔值列表，列表中每个元素依次分别对应 queries 每个查询对的判断结果。

注意：如果课程 a 是课程 b 的先修课程且课程 b 是课程 c 的先修课程，那么课程 a 也是课程 c 的先修课程。

示例 1：
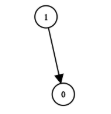
在这里插入图片描述

输入：n = 2, prerequisites = [[1,0]], 
queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

示例 2：
输入：n = 2, prerequisites = [], 
queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

示例 3：
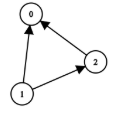
在这里插入图片描述

输入：n = 3, prerequisites = [[1,2],[1,0],[2,0]], 
queries = [[1,0],[1,2]]
输出：[true,true]示例 4：
输入：n = 3, prerequisites = [[1,0],[2,0]], 
queries = [[0,1],[2,0]]
输出：[false,true]示例 5：
输入：n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], 
queries = [[0,4],[4,0],[1,3],[3,0]]
输出：[true,false,true,false]提示：
2 <= n <= 100
0 <= prerequisite.length <= (n * (n - 1) / 2)
0 <= prerequisite[i][0], prerequisite[i][1] < n
prerequisite[i][0] != prerequisite[i][1]
先修课程图中没有环。
先修课程图中没有重复的边。
1 <= queries.length <= 10^4
queries[i][0] != queries[i][1]

解答：

参考弗洛伊德算法，多点源之间的最短路径，时间复杂度 $O(V^3)$
注意 i,j,k 的顺序

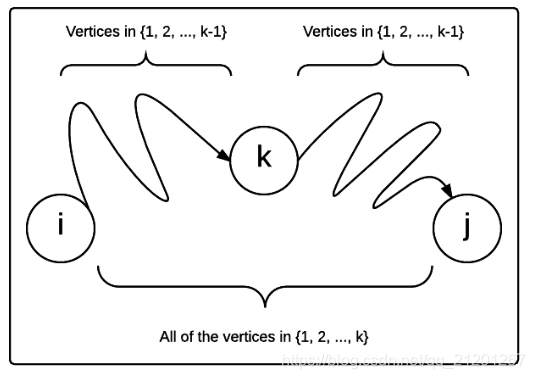
在这里插入图片描述

For each cell (i, j) in M:if i == j:M[i][j] = 0if (i, j) is an edge in E:M[i][j] = weight(i, j)else:M[i][j] = infinity
for k from 1 to |V|:for i from 1 to |V|:for j from 1 to |V|:if M[i][j] > M[i][k] + M[k][j]:M[i][j] = M[i][k] + M[k][j]

class Solution {
public:vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {vector<vector<bool>> m(n, vector<bool>(n,false));for(auto& pre : prerequisites)m[pre[0]][pre[1]] = true;int i, j, k;for(i = 0; i < n; ++i){for(j = 0; j < n; ++j){for(k = 0; k < n; ++k){if(m[j][i] && m[i][k])//连通判断m[j][k] = true;}}}vector<bool> ans(queries.size());i = 0;for(auto& q : queries)ans[i++] = m[q[0]][q[1]];return ans;}
};

1068 ms 59.5 MB

4. LeetCode 5411. 摘樱桃 II hard

题目链接
给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。

你有两个机器人帮你收集樱桃，机器人 1 从左上角格子 (0,0) 出发，机器人 2 从右上角格子 (0, cols-1) 出发。

请你按照如下规则，返回两个机器人能收集的最多樱桃数目：

从格子 (i,j) 出发，机器人可以移动到格子 (i+1, j-1)，(i+1, j) 或者 (i+1, j+1) 。
当一个机器人经过某个格子时，它会把该格子内所有的樱桃都摘走，然后这个位置会变成空格子，即没有樱桃的格子。
当两个机器人同时到达同一个格子时，它们中只有一个可以摘到樱桃。
两个机器人在任意时刻都不能移动到 grid 外面。
两个机器人最后都要到达 grid 最底下一行。

示例 1：
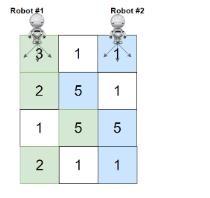
在这里插入图片描述

输入：grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
输出：24
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12 。
机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12 。
樱桃总数为： 12 + 12 = 24 。

示例 2：
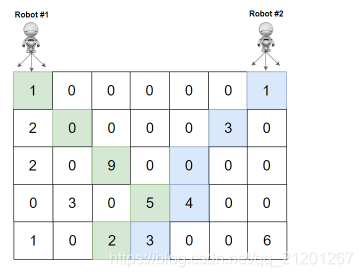
在这里插入图片描述

输入：grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
输出：28
解释：机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17 。
机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11 。
樱桃总数为： 17 + 11 = 28 。示例 3：
输入：grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
输出：22示例 4：
输入：grid = [[1,1],[1,1]]
输出：4提示：
rows == grid.length
cols == grid[i].length
2 <= rows, cols <= 70
0 <= grid[i][j] <= 100

解题：

状态定义很难，参考的大佬们的思路
dp[i][j1][j2],表示第 i 层，两机器人位置为 j1 , j2 的最大值

class Solution {
public:int cherryPickup(vector<vector<int>>& grid) {int i, j1, j2, nj1, nj2,k1,k2, m = grid.size(), n = grid[0].size();vector<vector<vector<int>>> dp(m,vector<vector<int>>(n, vector<int>(n,-1)));//dp[i][j1][j2],表示第i层，两机器人位置为 j1, j2 的最大值dp[0][0][n-1] = grid[0][0]+grid[0][n-1];vector<int> dir = {-1,0,1};int maxPick = 0;for(i = 1; i < m; ++i){for(j1 = 0; j1 < n; ++j1){for(j2 = 0; j2 < n; ++j2){if(dp[i-1][j1][j2] != -1){for(k1 = 0; k1 < 3; ++k1){nj1 = j1 + dir[k1];for(k2 = 0; k2 < 3; ++k2){nj2 = j2 + dir[k2];if(nj1 >= 0 && nj1 < n && nj2 >= 0 && nj2 < n){if(nj1 == nj2)dp[i][nj1][nj2] = max(dp[i][nj1][nj2], dp[i-1][j1][j2]+grid[i][nj1]);elsedp[i][nj1][nj2] = max(dp[i][nj1][nj2], dp[i-1][j1][j2]+grid[i][nj1]+grid[i][nj2]);	}}}}}    			}}for(j1 = 0; j1 < n; ++j1)for(j2 = 0; j2 < n; ++j2)maxPick = max(maxPick, dp[m-1][j1][j2]);return maxPick;}
};