1. 题目

给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。

请你返回元素总和小于或等于阈值的正方形区域的最大边长；
如果没有这样的正方形区域，则返回 0 。

示例 1：
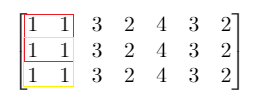
输入：mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], 
threshold = 4
输出：2
解释：总和小于 4 的正方形的最大边长为 2，如图所示。示例 2：
输入：mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], 
threshold = 1
输出：0示例 3：
输入：mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], 
threshold = 6
输出：3示例 4：
输入：mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], 
threshold = 40184
输出：2提示：
1 <= m, n <= 300
m == mat.length
n == mat[i].length
0 <= mat[i][j] <= 10000
0 <= threshold <= 10^5

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

• 先求出左上角（0,0）到任意位置组成的矩形的和
• 然后遍历所有的 左上顶点，再遍历正方形的边长
• 时间复杂度 $O(mn\ast min(m,n))$

class Solution {
public:int maxSideLength(vector<vector<int>>& mat, int threshold) {int m = mat.size(), n = mat[0].size(), i, j, maxlen = 0, len = 0;vector<vector<int>> sum(m,vector<int>(n,0));//先求第一行、第一列的前缀和for(j = 0; j < n; ++j)sum[0][j] = (j > 0 ? sum[0][j-1] : 0) + mat[0][j];//注意加括号for(i = 1; i < m; ++i)sum[i][0] = sum[i-1][0] + mat[i][0];//剩余位置的前缀和for(i = 1; i < m; ++i)for(j = 1; j < n; ++j)sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1]+mat[i][j];int ni, nj, sumofarea;//遍历左上角位置for(i = 0; i < m; ++i)for(j = 0; j < n; ++j)for(len = 1; len <= min(m,n); ++len){	//遍历正方形边长ni = i+len-1;//右下角nj = j+len-1;if(ni < m && nj < n){sumofarea = sum[ni][nj]-(i>0?sum[i-1][nj]:0)-(j>0?sum[ni][j-1]:0)+((i>0&&j>0) ? sum[i-1][j-1] : 0);//由前缀和推出正方形的和if(sumofarea <= threshold){maxlen = max(maxlen, len);if(maxlen == min(m,n))return maxlen;}}elsebreak;}return maxlen;}
};

1104 ms 22.6 MB

• 优化，下一个顶点，遍历的长度从maxlen+1开始找
• 和是增大的，一旦大于阈值就不必往下找了
• 这种解法的时间复杂度为 $O(mn)$，可以参考官方题解分析，比最内层循环采用二分查找的方式$O(mn\log (min(m,n))$更优

class Solution {
public:int maxSideLength(vector<vector<int>>& mat, int threshold) {int m = mat.size(), n = mat[0].size(), i, j, maxlen = 0, len = 0;vector<vector<int>> sum(m,vector<int>(n,0));for(j = 0; j < n; ++j)sum[0][j] = (j > 0 ? sum[0][j-1] : 0) + mat[0][j];for(i = 1; i < m; ++i)sum[i][0] = sum[i-1][0] + mat[i][0];for(i = 1; i < m; ++i)for(j = 1; j < n; ++j)sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1]+mat[i][j];int ni, nj, sumofarea;for(i = 0; i < m; ++i)for(j = 0; j < n; ++j)for(len = maxlen+1; len <= min(m,n); ++len){ni = i+len-1;nj = j+len-1;if(ni < m && nj < n && sum[ni][nj]-(i>0?sum[i-1][nj]:0)-(j>0?sum[ni][j-1]:0)+(i>0&&j>0 ? sum[i-1][j-1] : 0) <= threshold){maxlen = max(maxlen, len);if(maxlen == min(m,n))return maxlen;}elsebreak;}return maxlen;}
};

176 ms 22.5 MB

python3 解答

class Solution:# py3def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:m, n = len(mat), len(mat[0])maxlen = 0prefixsum = [[0]*n for _ in range(m)]prefixsum[0][0] = mat[0][0]for j in range(1,n):prefixsum[0][j] = prefixsum[0][j-1]+mat[0][j]for i in range(1,m):prefixsum[i][0] = prefixsum[i-1][0]+mat[i][0]for i in range(1,m):for j in range(1,n):prefixsum[i][j] = prefixsum[i-1][j]+prefixsum[i][j-1]-prefixsum[i-1][j-1]+mat[i][j]for i in range(m):for j in range(n):length = maxlen+1while length <= min(m,n):ni = i+length-1nj = j+length-1if ni<m and nj<n and prefixsum[ni][nj]-(prefixsum[i-1][nj] if i > 0 else 0)-(prefixsum[ni][j-1] if j > 0 else 0)+(prefixsum[i-1][j-1] if i>0 and j>0 else 0) <= threshold:maxlen = max(maxlen, length)if maxlen == min(m,n):return maxlenelse:breaklength += 1return maxlen

1092 ms 19.3 MB