本文为《机器学习实战：基于Scikit-Learn和TensorFlow》的读书笔记。
中文翻译参考

1. 线性回归

如何得到模型的参数

1.1 正规方程求解

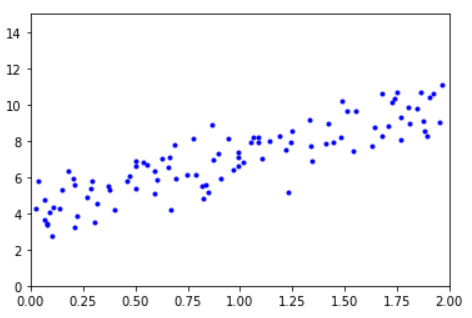
• 先生成带噪声的线性数据

import numpy as np
import matplotlib.pyplot as plt
X = 2*np.random.rand(100,1)
y = 4+3*X+np.random.randn(100,1)
plt.plot(X,y,"b.")
plt.axis([0,2,0,15])

• 采用矩阵解方程，得到参数

X_b = np.c_[np.ones((100,1)),X]
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best

array([[4.46927218],[2.71589368]])

• 预测新的数据

X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)),X_new]
y_pred = X_new_b.dot(theta_best)
y_pred

array([[4.46927218],[9.90105954]])

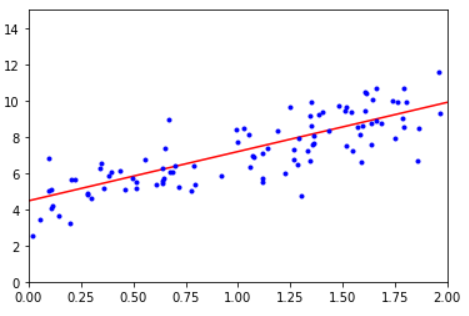
• 画出模型回归线

plt.plot(X_new,y_pred,"r-")
plt.plot(X,y,"b.")
plt.axis([0,2,0,15])
plt.show()

• 使用sklearn求解

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
lin_reg.intercept_, lin_reg.coef_ # (array([4.15725481]), array([[2.97840411]]))
lin_reg.predict(X_new)

array([[ 4.15725481],[10.11406304]])

1.2 时间复杂度

求解过程需要矩阵求逆，矩阵求逆时间复杂度在 $O(n^{2.4})$ 到 $O(n^3)$ 之间，n 为特征数

• 特征个数很多的时候，这种计算方法将会非常慢

1.3 梯度下降

整体思路：通过的迭代来逐渐调整参数使得损失函数达到最小值

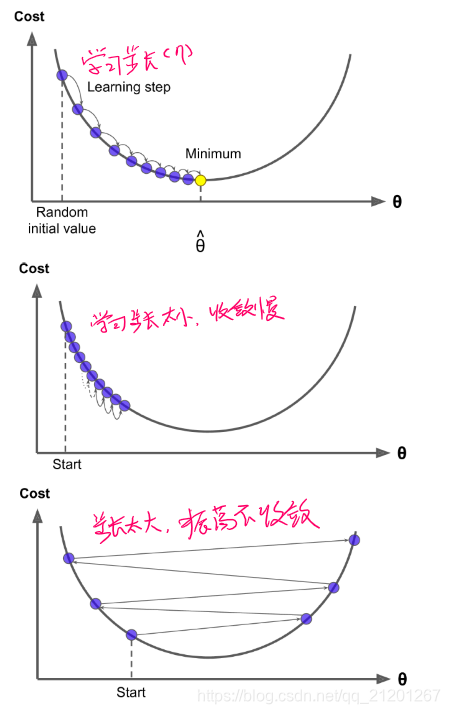
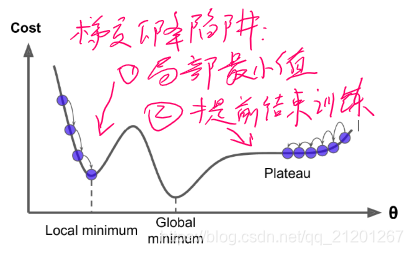
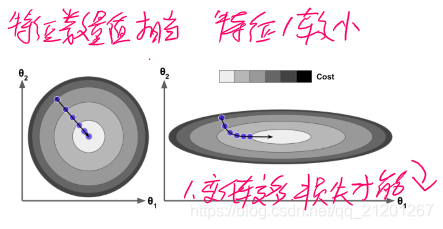
由上图右侧可见，一开始的方向跟梯度方向几乎垂直，走了弯路。

当我们使用梯度下降的时候，应该确保所有的特征有着相近的尺度范围

（例如：使用 Scikit Learn 的 StandardScaler类），否则它将需要很长的时间才能够收敛。

• 参数越多，找到最佳参数的难度也越大

1.4 批量梯度下降

• 会使用全部的训练数据
• 在大数据集上会变得很慢

eta = 0.1 # 学习率
n_iter = 1000
m = 100
theta = np.random.randn(2,1)for iter in range(n_iter):gradients = 2/m*X_b.T.dot(X_b.dot(theta)-y)theta = theta - eta*gradients
theta

array([[4.33118102],[2.8597418 ]])

• 不同的学习率下，学习情况对比

eta = 0.1 # 学习率
n_iter = 1000
m = 100
theta = np.random.randn(2,1)plt.figure(figsize=(8,6))
plt.ion()# 打开交互模式
plt.axis([0,2,0,15])
plt.rcParams["font.sans-serif"] = "SimHei"for iter in range(n_iter):plt.cla() # 清除原图像gradients = 2/m*X_b.T.dot(X_b.dot(theta)-y)theta = theta - eta*gradientsX_new = np.array([[0],[2]])X_new_b = np.c_[np.ones((2,1)),X_new]y_pred = X_new_b.dot(theta)plt.plot(X,y,"b.")plt.plot(X_new,y_pred,"r-")plt.title("学习率：{:.2f}".format(eta))plt.pause(0.1) # 暂停一会display.clear_output(wait=True)# 刷新图像
plt.ioff()# 关闭交互模式    
plt.show()
theta

求解过程动图请参看博文：matplotlib 绘制梯度下降求解过程

• 实际使用时，设置较大的迭代次数，和容差，当梯度向量变得非常小的时候，小于容差时，认为收敛，结束迭代

1.5 随机梯度下降

每一步梯度计算只随机选取训练集中的一个样本。这使得算法变得非常快。

• 随机梯度算法可以在大规模训练集上使用
• 由于随机性，它到达最小值不是平缓下降，损失函数会忽高忽低，大体呈下降趋势
• 迭代点不会停止在一个值上，会一直在这个值附近摆动，最后的参数还不错，但不是最优值

由于其随机性，它能跳过局部最优解，但同时它却不能达到最小值。

解决办法：逐渐降低学习率

• 开始时，走大步，快速前进+跳过局部最优解
• 然后逐步降低学习率，使算法到达全局最小值。 这个过程被称为模拟退火，因为它类似于熔融金属慢慢冷却的冶金学退火过程

决定每次迭代的学习率的函数称为 learning schedule

• 如果学习速度降得过快，可能陷入局部最小值，或者迭代次数到了半路就停止了
• 如果学习速度降得太慢，可能在最小值附近震荡，如果过早停止训练，只得到次优解

from sklearn.linear_model import SGDRegressor
# help(SGDRegressor)
sgd_reg = SGDRegressor(max_iter=100, penalty=None, eta0=0.1)
sgd_reg.fit(X,y.ravel())
sgd_reg.intercept_, sgd_reg.coef_

(array([3.71001759]), array([2.99883799]))

1.6 小批量梯度下降

每次迭代的时候，使用一个随机的小型实例集

2. 多项式回归

依然可以使用线性模型来拟合非线性数据

• 一个简单的方法：对每个特征进行加权后作为新的特征
• 然后训练一个线性模型基于这个扩展的特征集。 这种方法称为多项式回归。

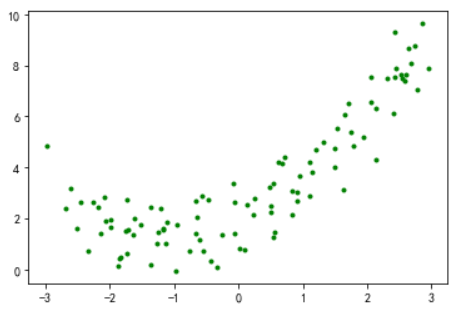
m = 100
X = 6*np.random.rand(m,1)-3
y = 0.5*X**2 + X + 2 + np.random.randn(m,1)
plt.rcParams["axes.unicode_minus"] = False # 显示负号
plt.plot(X, y, "g.")

from sklearn.preprocessing import PolynomialFeatures
pf = PolynomialFeatures(degree=2, include_bias=False)
# help(PolynomialFeatures)
X_ploy = pf.fit_transform(X)
print(X[0])
print(X_ploy[0])

• 对原始特征进行2阶多项式转换后，多出了 X² 项

[2.43507761]
[2.43507761 5.92960298]

• 进行线性回归

lin_reg = LinearRegression()
lin_reg.fit(X_ploy, y)
lin_reg.intercept_, lin_reg.coef_

(array([1.95147614]), array([[1.0462516 , 0.48003845]]))

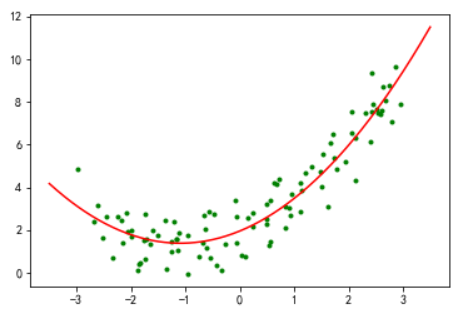
• 绘出预测线

plt.plot(X, y, "g.")
x = np.linspace(-3.5, 3.5, 500)
print(x.shape)
y_pred = lin_reg.intercept_ + lin_reg.coef_[0][0]*x + lin_reg.coef_[0][1]*x**2
plt.plot(x, y_pred, 'r-')

注意，阶数变大时，特征的维度会急剧上升，不仅有 $a^n$，还有 $a^{n-1}b,a^{n-2}{b}^2$等

如何确定选择多少阶：

1、交叉验证

• 在训练集上表现良好，但泛化能力很差，过拟合
• 如果这两方面都不好，欠拟合。可知模型是太复杂还是太简单

2、观察学习曲线

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_splitdef plot_learning_curves(model, X, y):X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)train_errors, val_errors = [], []for m in range(1, len(X_train)):model.fit(X_train[:m], y_train[:m])y_train_predict = model.predict(X_train[:m])y_val_predict = model.predict(X_val)train_errors.append(mean_squared_error(y_train_predict, y_train[:m]))val_errors.append(mean_squared_error(y_val_predict, y_val))plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)

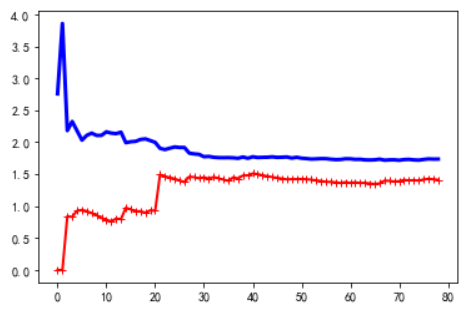
• 上图显示训练集和测试集在数据不断增加的情况下，曲线趋于稳定，同时误差都非常大，欠拟合
• 欠拟合，添加样本是没用的，需要更复杂的模型或更好的特征

模型的泛化误差由三个不同误差的和决定：

• 偏差：模型假设不贴合，高偏差的模型最容易出现欠拟合
• 方差：模型对训练数据的微小变化较为敏感，多自由度的模型更容易有高的方差（如高阶多项式），会导致过拟合
• 不可约误差：数据噪声，可进行数据清洗

3. 线性模型正则化

限制模型的自由度，降低过拟合

• 岭（Ridge）回归 L2正则
• Lasso 回归 L1正则
• 弹性网络（ElasticNet），以上两者的混合，r=0, 就是L2，r=1，就是 L1
  $$J(\theta )=MSE(\theta )+r\alpha \sum _{i=1}^n\left|{\theta }_i\right|+\frac{1-r}{2}\alpha \sum _{i=1}^n{\theta }_i^2$$

from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]]) # array([[5.04581676]])from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])  # array([5.00189893])from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]]) # array([4.99822842])

4. 早期停止法（Early Stopping）

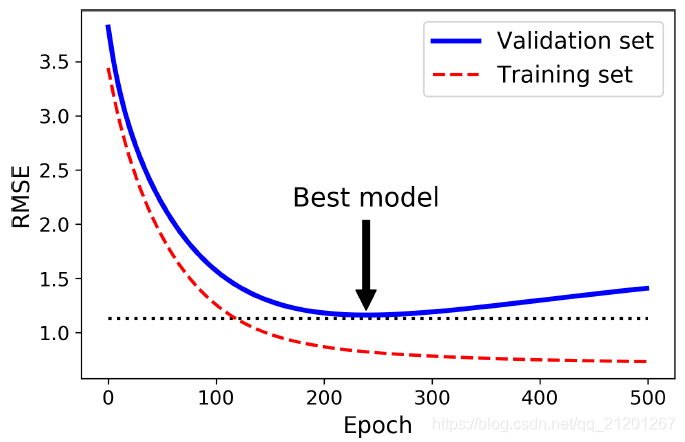
验证集 误差达到最小值，并开始上升时（出现过拟合），结束迭代，回滚到之前的最小值处