LeetCode 1516. Move Sub-Tree of N-Ary Tree（DFS）

文章目录

- 1. 题目
- 2. 解题

1. 题目

Given the root of an N-ary tree of unique values, and two nodes of the tree p and q.

You should move the subtree of the node p to become a direct child of node q. If p is already a direct child of q, don’t change anything. Node p must be the last child in the children list of node q.

Return the root of the tree after adjusting it.

There are 3 cases for nodes p and q:

Node q is in the sub-tree of node p.
Node p is in the sub-tree of node q.
Neither node p is in the sub-tree of node q nor node q is in the sub-tree of node p.

In cases 2 and 3, you just need to move p (with its sub-tree) to be a child of q, but in case 1 the tree may be disconnected, thus you need to reconnect the tree again. Please read the examples carefully before solving this problem.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).
在这里插入图片描述
For example, the above tree is serialized as [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14].

Example 1:
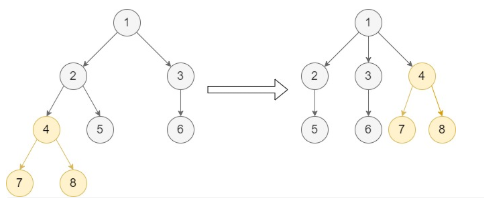
在这里插入图片描述

Input: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 4, q = 1
Output: [1,null,2,3,4,null,5,null,6,null,7,8]
Explanation: This example follows the second case as node p is in the sub-tree of node q. We move node p with its sub-tree to be a direct child of node q.
Notice that node 4 is the last child of node 1.

Example 2:
在这里插入图片描述

Input: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 7, q = 4
Output: [1,null,2,3,null,4,5,null,6,null,7,8]
Explanation: Node 7 is already a direct child of node 4. We don’t change anything.

Example 3:
在这里插入图片描述

Input: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 3, q = 8
Output: [1,null,2,null,4,5,null,7,8,null,null,null,3,null,6]
Explanation: This example follows case 3 because node p is not in the sub-tree of node q and vice-versa. We can move node 3 with its sub-tree and make it as node 8’s child.

Example 4:
在这里插入图片描述

Input: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 2, q = 7
Output: [1,null,7,3,null,2,null,6,null,4,5,null,null,8]
Explanation: Node q is in the sub-tree of node p, so this is case 1.
The first step, we move node p (with all of its sub-tree except for node q) and add it as a child to node q.
Then we will see that the tree is disconnected, you need to reconnect node q to replace node p as shown.

Example 5:
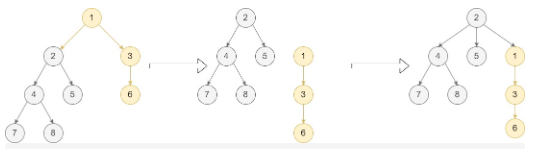
在这里插入图片描述

Input: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 1, q = 2
Output: [2,null,4,5,1,null,7,8,null,null,3,null,null,null,6]
Explanation: Node q is in the sub-tree of node p, so this is case 1.
The first step, we move node p (with all of its sub-tree except for node q) and add it as a child to node q.
As node p was the root of the tree, node q replaces it and becomes the root of the tree.

Constraints:
The total number of nodes is between [2, 1000].
Each node has a unique value.
p != null
q != null
p and q are two different nodes (i.e. p != q).

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/move-sub-tree-of-n-ary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

先看下 p 在不在 q 的直接子节点里，在的话直接返回
再 DFS 确定 q 是不是 p 的子树节点，以及找到 p\q 的父节点
再分两种情况讨论，见注释

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {Node *pf = NULL, *qf = NULL;//父节点bool qisSubOfp = false;bool foundp = false;bool foundq = false;
public:Node* moveSubTree(Node* root, Node* p, Node* q) {for(auto node : q->children)if(node == p)//p是q的直接子节点，无需操作return root;Node* empty = new Node(-1);//建立空节点方便处理empty->children.push_back(root);dfs(empty, NULL, p, q);//q 不是 p 的子节点，p肯定不是rootif(!qisSubOfp){//找到 pf 子节点 p 的 iterauto it = find(pf->children.begin(),pf->children.end(),p);pf->children.erase(it);//删除之q->children.push_back(p);//p接到q的子节点中return root;}//q 是 p 的子树节点，p可能是rootauto it = find(qf->children.begin(),qf->children.end(),q);qf->children.erase(it);//断开 q 与 qfit = find(pf->children.begin(),pf->children.end(),p);//断开 p 与 pfit = pf->children.erase(it);//it指向下一个，即 pf child 中 p 的下一个位置q->children.push_back(p);//接入到q下面pf->children.insert(it, q);//pf 的子节点 原来 p 的位置 插入 qreturn empty->children[0];}void dfs(Node* root, Node* fa, Node* p, Node* q){if(!root) return;if(root == p){pf = fa;foundp = true;}if(root == q){if(foundp)qisSubOfp = true;qf = fa;foundq = true;}for(auto c : root->children)dfs(c, root, p, q);if(root == p)foundp = false;//回溯if(root == q)foundq = false;//回溯}   
};