1. 题目

在由 2D 网格表示的校园里有 n 位工人（worker）和 m 辆自行车（bike），n <= m。所有工人和自行车的位置都用网格上的 2D 坐标表示。

我们需要为每位工人分配一辆自行车。在所有可用的自行车和工人中，我们选取彼此之间曼哈顿距离最短的工人自行车对 (worker, bike) ，并将其中的自行车分配給工人。
如果有多个 (worker, bike) 对之间的曼哈顿距离相同，那么我们选择工人索引最小的那对。
类似地，如果有多种不同的分配方法，则选择自行车索引最小的一对。
不断重复这一过程，直到所有工人都分配到自行车为止。

给定两点 p1 和 p2 之间的曼哈顿距离为 Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|。

返回长度为 n 的向量 ans，其中 a[i] 是第 i 位工人分配到的自行车的索引（从 0 开始）。

示例 1：

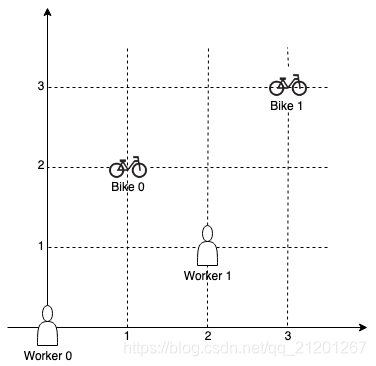
输入：workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]]
输出：[1,0]
解释：
工人 1 分配到自行车 0，因为他们最接近且不存在冲突，工人 0 分配到自行车 1 。
所以输出是 [1,0]。

示例 2：

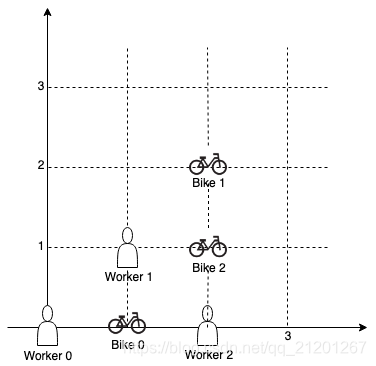
输入：workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]]
输出：[0,2,1]
解释：
工人 0 首先分配到自行车 0 。
工人 1 和工人 2 与自行车 2 距离相同，因此工人 1 分配到自行车 2，工人 2 将分配到自行车 1 。
因此输出为 [0,2,1]。提示：
0 <= workers[i][j], bikes[i][j] < 1000
所有工人和自行车的位置都不相同。
1 <= workers.length <= bikes.length <= 1000

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/campus-bikes
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

• 贪心，先选择小的距离，选择了则记录已经有自行车的人，和自行车被访问过了
• 使用map，key有序，key 为距离，value 为 工人idx，自行车 idx

class Solution {
public:vector<int> assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {map<int,vector<vector<int>>> dis_w_b;int dis, count = 0;for(int i = 0; i < workers.size(); i++){for(int j = 0; j < bikes.size(); j++){dis = abs(workers[i][0]-bikes[j][0])+ abs(workers[i][1]-bikes[j][1]);dis_w_b[dis].push_back(vector<int>({i,j}));}}vector<bool> vis_b(bikes.size(), false);vector<int> ans(workers.size(), -1);for(auto it = dis_w_b.begin(); it != dis_w_b.end(); ++it){	//按距离从小到大for(int i = 0; i < it->second.size(); ++i){	//遍历该距离下所有的 组合if(ans[it->second[i][0]] != -1 || vis_b[it->second[i][1]])continue;//有自行车了，或者自行车被占用了ans[it->second[i][0]] = it->second[i][1];vis_b[it->second[i][1]] = true;if(++count == workers.size())break;}}return ans;}
};

1480 ms 144 MB

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！