LeetCode 1066. 校园自行车分配 II（状态压缩DP）

文章目录

- 1. 题目
- 2. 解题
- - 2.1 回溯超时
  - 2.2 状态压缩DP

1. 题目

在由 2D 网格表示的校园里有 n 位工人（worker）和 m 辆自行车（bike），n <= m。所有工人和自行车的位置都用网格上的 2D 坐标表示。

我们为每一位工人分配一辆专属自行车，使每个工人与其分配到的自行车之间的曼哈顿距离最小化。

p1 和 p2 之间的曼哈顿距离为 Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|。

返回每个工人与分配到的自行车之间的曼哈顿距离的最小可能总和。

示例 1：
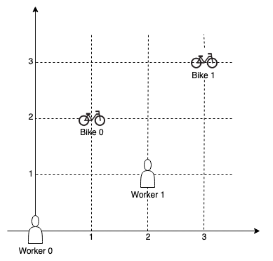
在这里插入图片描述

输入：workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]]
输出：6
解释：
自行车 0 分配给工人 0，自行车 1 分配给工人 1 。
分配得到的曼哈顿距离都是 3, 所以输出为 6 。

示例 2：
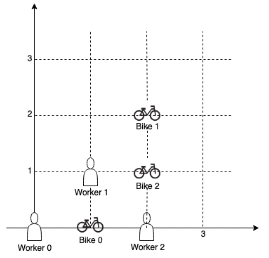
在这里插入图片描述

输入：workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]]
输出：4
解释：
先将自行车 0 分配给工人 0，
再将自行车 1 分配给工人 1（或工人 2），
自行车 2 给工人 2（或工人 1）。
如此分配使得曼哈顿距离的总和为 4。提示：
0 <= workers[i][0], workers[i][1], bikes[i][0], bikes[i][1] < 1000
所有工人和自行车的位置都不相同。
1 <= workers.length <= bikes.length <= 10

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/campus-bikes-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

2.1 回溯超时

22 / 44 个通过测试用例

class Solution {int mindis = INT_MAX;
public:int assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {int nw = workers.size(), nb = bikes.size(), i, j;vector<vector<int>> dis(nw, vector<int>(nb));vector<bool> vis(nb, false);for(i = 0; i < nw; ++i)for(j = 0; j < nb; ++j)dis[i][j] = abs(workers[i][0]-bikes[j][0])+ abs(workers[i][1]-bikes[j][1]);dfs(workers, bikes, vis, dis, 0, 0);return mindis;}void dfs(vector<vector<int>>& workers, vector<vector<int>>& bikes,vector<bool> &vis, vector<vector<int>> &dis, int idx, int distance){if(idx == workers.size()){mindis = min(mindis, distance);return;}for(int i = 0; i < bikes.size(); ++i){if(vis[i]) continue;vis[i] = true;if(distance < mindis)dfs(workers, bikes, vis, dis, idx+1, distance+dis[idx][i]);vis[i] = false;}}
};

2.2 状态压缩DP

参考大力王的题解

类似题目：LeetCode 5387. 每个人戴不同帽子的方案数 hard

class Solution {
public:int assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {int m = workers.size(), n = bikes.size(), i, j;vector<vector<int>> dis(m, vector<int>(n));for(i = 0; i < m; ++i)for(j = 0; j < n; ++j)dis[i][j] = abs(workers[i][0]-bikes[j][0])+ abs(workers[i][1]-bikes[j][1]);int M = 1 << m, N = 1 << n;//每个人或者自行车都看成一个二进制位，0还没选，1选了vector<vector<int>> dp(M, vector<int>(N, 1000000));for(i = 0; i < m; ++i)for(j = 0; j < n; ++j)dp[1<<i][1<<j] = dis[i][j];for(i = 0; i < M; ++i)for(j = 0; j < N; ++j){int i_ = i, j_ = j;m = i&(-i);//二进制数最后一个1代表的数值lowbitn = j&(-j);while(m > 0)//遍历之前的人的状态{dp[i][j] = min(dp[i][j], dp[i-m][j-n]+dp[m][n]);//i-m表示少了？个1，少了？个人//j-n表示少了？辆车i_ -= m;//减掉一个人m = i_&(-i_);}m = i&(-i);//二进制数最后一个1代表的数值lowbitn = j&(-j);while(n > 0)//遍历之前的车子状态{dp[i][j] = min(dp[i][j], dp[i-m][j-n]+dp[m][n]);//i-m表示少了？个1，少了？个人//j-n表示少了？辆车j_ -= n;//减掉一辆车n = j_&(-j_);}}return *min_element(dp[M-1].begin(), dp[M-1].end());}
};