1. 题目

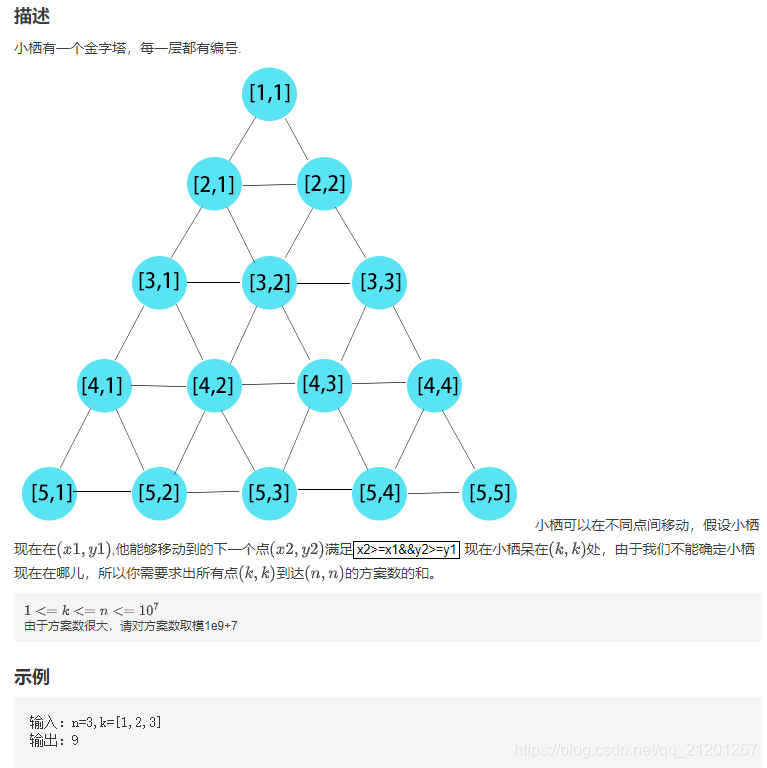
来源：https://tianchi.aliyun.com/oj/15165469968503404/76745683739284070

2. 解题

按道理可以DP暴力求解，但是数据规模太大，会超时的

手算前几项，然后去 oesi 网站查询数列，找到 大施罗德数，就是本题的答案

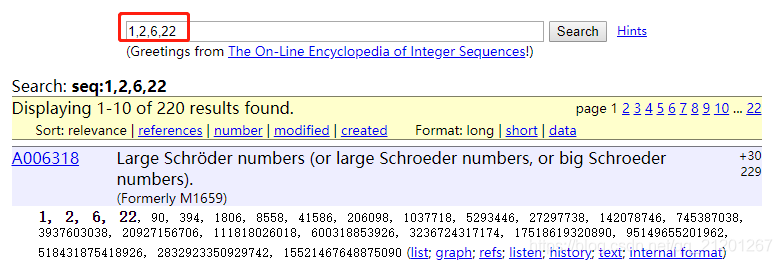
但是这个数列的递推公式是： $$F_n=F_{n-1}+\sum _{k=0}^{n-1}{F}_k\ast F_{n-1-k}$$

是 $O(n^2)$ 时间复杂度，会超时

又查到 超级卡特兰数： $$F_n\ast (n+1)=(6\ast n-3)\ast F_{n-1}-(n-2)\ast F_{n-2}$$

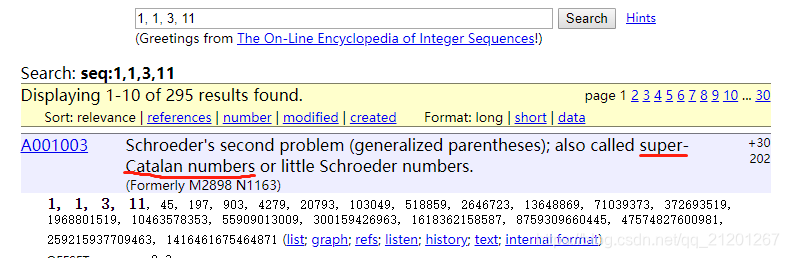
发现，除了第 0 项以外，超级卡特兰数 X 2 = 大施罗德数。厉害！

---

另外，超级卡特兰数，要求 $F_n$ 要除以 $(n+1)$，要用到除法的求模转换方法。
除法是无法直接求模的。有以下方法。

除法求模 + 快速幂

a / c mod p
= a / c mod p * 1
= a / c mod p * c^(p-1) mod p
= a * c^(p-2) mod p

或者 乘法逆元法

inv[1] = 1;
for (int i = 2; i <= n; ++i)
{inv[i] = (mod - mod/i) * inv[mod%i] % mod;//求模运算的乘法逆元
}

---

解答：

class Solution {vector<long long> catalan;int mod = 1e9+7;
public:/*** @param n: The number of pyramid levels n* @param k: Possible coordinates k* @return: Find the sum of the number of plans*/int pyramid(int n, vector<int> &k) {// write your code herelong long sum = 0;catalan = vector<long long>(n+1, 0);catalan[0] = 1;catalan[1] = 1;vector<long long> inv(n+1);inv[1] = 1;for (int i = 2; i <= n; ++i){inv[i] = (mod - mod/i) * inv[mod%i] % mod;//求模运算的乘法逆元}for(int i = 2; i <= n; i++){catalan[i] = ((catalan[i-1]*(6*i-3)%mod)-((i-2)*catalan[i-2]%mod)+mod)*inv[i+1]%mod;}for(int i = 0; i < k.size(); i++){sum = (sum+cal(n,k[i]))%mod;}return sum;}long long cal(int n, int k){if(n == k) return 1;return (catalan[n-k]*2)%mod;}
};

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！