模型函数介绍
Logistic Regression 虽然被称为回归,但其实际上是分类模型,并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱。
Logistic 回归的本质是:假设数据服从这个Logistic 分布,然后使用极大似然估计方法做参数的估计。
Logistic 分布是一种连续型的概率分布,其分布函数和密度函数分别为:
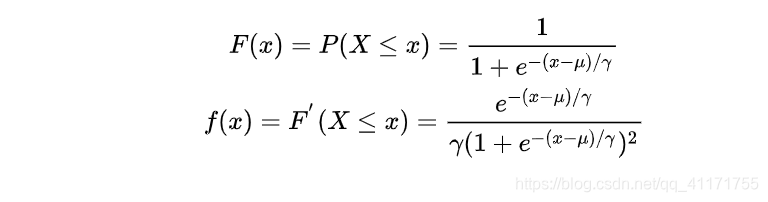
其中, ![]() 表示位置参数,
表示位置参数, ![]() 为形状参数。我们可以看下其图像特征:
为形状参数。我们可以看下其图像特征:
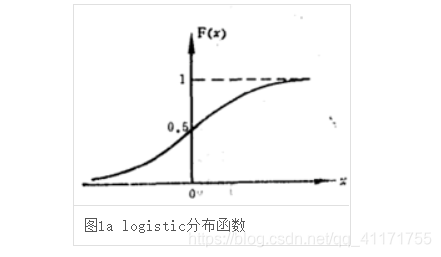
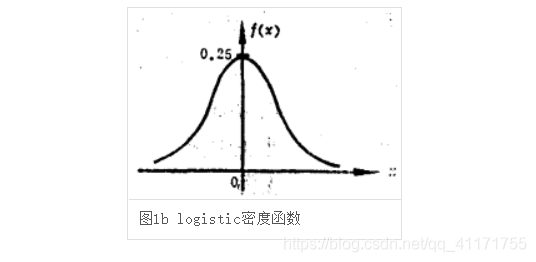
在逻辑斯谛回归中,使用逻辑斯谛函数
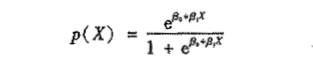
然后用极大似然估计( maximum likelihood) 方法拟合模型 。
模型运用
我们运用 ISLR 库的 smarket (股旗市场)数据的数值和图像进行描述统计分析,来拟合逻辑斯蒂归模型。该数据集里包括了从 2001 年年初至 2005 年年末 1250 天里 S&P 500 股票指数的投资回报率。数据中记 录了过去 5 个交易日中的每个交易日的投资回报率,从 Lag1到 Lag5 ,同时也记录了 Volume (前一日股票成交量,单位为十亿) ,Today (当日的投资回报率)以及Direction (这些数据在市场的走势方向,或 Up (涨)或 Down (跌) )。
> library(ISLR)
> names(Smarket)
[1] "Year" "Lag1" "Lag2" "Lag3" "Lag4"
[6] "Lag5" "Volume" "Today" "Direction"
> fix(Smarket)#lag1~lag5表示5个交易日的股票投资回报率
# [1] "Year" "Lag1" "Lag2" "Lag3" "Lag4"
# [6] "Lag5" "Volume" "Today" "Direction"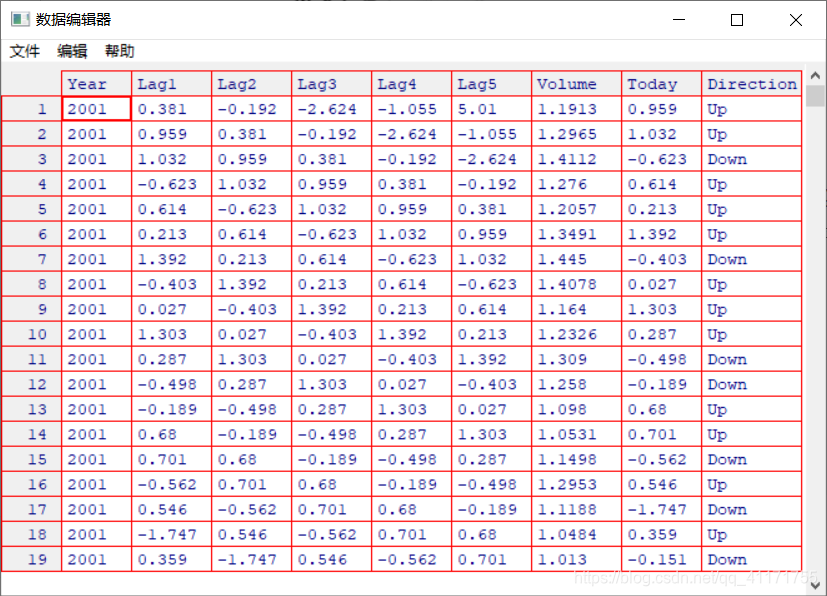
> dim(Smarket)
[1] 1250 9
> summary(Smarket)Year Lag1 Lag2 Min. :2001 Min. :-4.922000 Min. :-4.922000 1st Qu.:2002 1st Qu.:-0.639500 1st Qu.:-0.639500 Median :2003 Median : 0.039000 Median : 0.039000 Mean :2003 Mean : 0.003834 Mean : 0.003919 3rd Qu.:2004 3rd Qu.: 0.596750 3rd Qu.: 0.596750 Max. :2005 Max. : 5.733000 Max. : 5.733000 Lag3 Lag4 Lag5 Min. :-4.922000 Min. :-4.922000 Min. :-4.92200 1st Qu.:-0.640000 1st Qu.:-0.640000 1st Qu.:-0.64000 Median : 0.038500 Median : 0.038500 Median : 0.03850 Mean : 0.001716 Mean : 0.001636 Mean : 0.00561 3rd Qu.: 0.596750 3rd Qu.: 0.596750 3rd Qu.: 0.59700 Max. : 5.733000 Max. : 5.733000 Max. : 5.73300 Volume Today Direction Min. :0.3561 Min. :-4.922000 Down:602 1st Qu.:1.2574 1st Qu.:-0.639500 Up :648 Median :1.4229 Median : 0.038500 Mean :1.4783 Mean : 0.003138 3rd Qu.:1.6417 3rd Qu.: 0.596750 Max. :3.1525 Max. : 5.733000 > pairs(Smarket)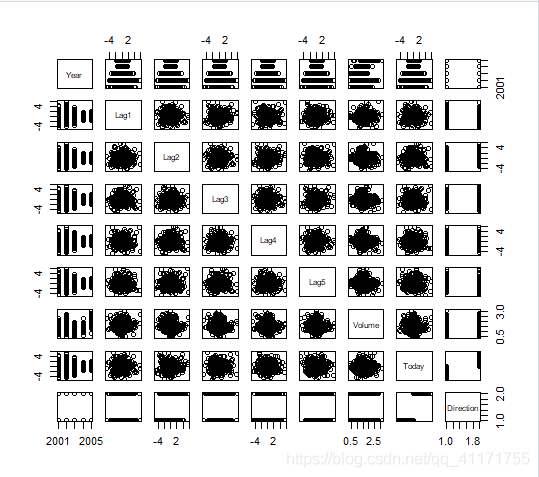
> cor(Smarket)#direction是定性的,所以出错
Error in cor(Smarket) : 'x'必需为数值cor(Smarket[,-9])#当前回报率与之前回报率相关性几乎为0Year Lag1 Lag2 Lag3 Lag4
Year 1.00000000 0.029699649 0.030596422 0.033194581 0.035688718
Lag1 0.02969965 1.000000000 -0.026294328 -0.010803402 -0.002985911
Lag2 0.03059642 -0.026294328 1.000000000 -0.025896670 -0.010853533
Lag3 0.03319458 -0.010803402 -0.025896670 1.000000000 -0.024051036
Lag4 0.03568872 -0.002985911 -0.010853533 -0.024051036 1.000000000
Lag5 0.02978799 -0.005674606 -0.003557949 -0.018808338 -0.027083641
Volume 0.53900647 0.040909908 -0.043383215 -0.041823686 -0.048414246
Today 0.03009523 -0.026155045 -0.010250033 -0.002447647 -0.006899527Lag5 Volume Today
Year 0.029787995 0.53900647 0.030095229
Lag1 -0.005674606 0.04090991 -0.026155045
Lag2 -0.003557949 -0.04338321 -0.010250033
Lag3 -0.018808338 -0.04182369 -0.002447647
Lag4 -0.027083641 -0.04841425 -0.006899527
Lag5 1.000000000 -0.02200231 -0.034860083
Volume -0.022002315 1.00000000 0.014591823
Today -0.034860083 0.01459182 1.000000000> attach(Smarket)
> plot(Volume)#volume随时间不断增长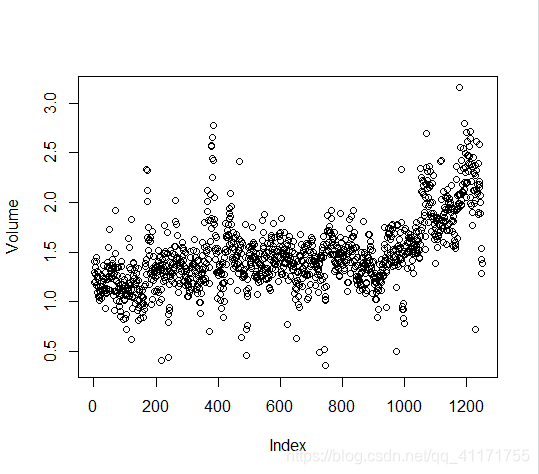
glm.fits=glm(Direction~Lag1+Lag2+Lag3+Lag4+Lag5+Volume,data=Smarket,family=binomial)
#glm函数用于拟合广义线性模型,family=binomial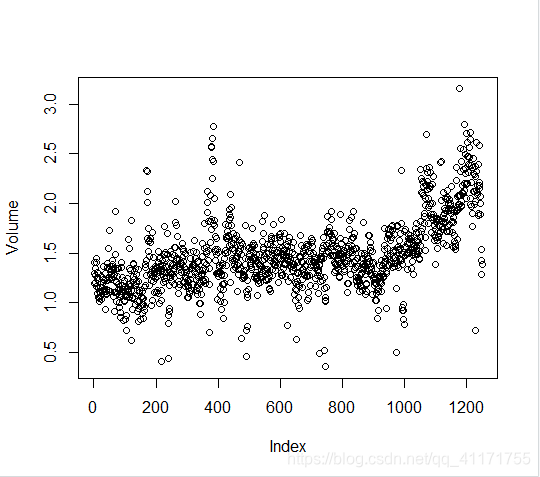
> summary(glm.fits)Call:
glm(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume, family = binomial, data = Smarket)Deviance Residuals: Min 1Q Median 3Q Max
-1.446 -1.203 1.065 1.145 1.326 Coefficients:Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.126000 0.240736 -0.523 0.601
Lag1 -0.073074 0.050167 -1.457 0.145
Lag2 -0.042301 0.050086 -0.845 0.398
Lag3 0.011085 0.049939 0.222 0.824
Lag4 0.009359 0.049974 0.187 0.851
Lag5 0.010313 0.049511 0.208 0.835
Volume 0.135441 0.158360 0.855 0.392(Dispersion parameter for binomial family taken to be 1)Null deviance: 1731.2 on 1249 degrees of freedom
Residual deviance: 1727.6 on 1243 degrees of freedom
AIC: 1741.6Number of Fisher Scoring iterations: 3> coef(glm.fits)#用于输出拟合模型系数(Intercept) Lag1 Lag2 Lag3 Lag4
-0.126000257 -0.073073746 -0.042301344 0.011085108 0.009358938 Lag5 Volume 0.010313068 0.135440659 > summary(glm.fits)$coefEstimate Std. Error z value Pr(>|z|)
(Intercept) -0.126000257 0.24073574 -0.5233966 0.6006983
Lag1 -0.073073746 0.05016739 -1.4565986 0.1452272
Lag2 -0.042301344 0.05008605 -0.8445733 0.3983491
Lag3 0.011085108 0.04993854 0.2219750 0.8243333
Lag4 0.009358938 0.04997413 0.1872757 0.8514445
Lag5 0.010313068 0.04951146 0.2082966 0.8349974
Volume 0.135440659 0.15835970 0.8552723 0.3924004> summary(glm.fits)$coef[,4]
(Intercept) Lag1 Lag2 Lag3 Lag4 Lag5 0.6006983 0.1452272 0.3983491 0.8243333 0.8514445 0.8349974 Volume 0.3924004 > glm.probs=predict(glm.fits,type="response")#type="response"表示明确输出概率
> glm.probs[1:10]1 2 3 4 5 6 7
0.5070841 0.4814679 0.4811388 0.5152224 0.5107812 0.5069565 0.4926509 8 9 10
0.5092292 0.5176135 0.4888378 > contrasts(Direction)#创建哑变量Up
Down 0
Up 1
> glm.pred=rep("Down",1250)
> glm.pred[glm.probs>.5]="Up"> table(glm.pred,Direction)#混淆矩阵Direction
glm.pred Down UpDown 145 141Up 457 507
> (507+145)/1250
[1] 0.5216
> mean(glm.pred==Direction)#表示正确预测的比例
[1] 0.5216> train=(Year<2005)
> Smarket.2005=Smarket[!train,]
> dim(Smarket.2005)
[1] 252 9> Direction.2005=Direction[!train]
> glm.fits=glm(Direction~Lag1+Lag2+Lag3+Lag4+Lag5+Volume,data=Smarket,family=binomial,subset=train)
> glm.probs=predict(glm.fits,Smarket.2005,type="response")
> glm.pred=rep("Down",252)
> glm.pred[glm.probs>.5]="Up"
> table(glm.pred,Direction.2005)Direction.2005
glm.pred Down UpDown 77 97Up 34 44
> mean(glm.pred==Direction.2005)
[1] 0.4801587
> mean(glm.pred!=Direction.2005)
[1] 0.5198413> glm.fits=glm(Direction~Lag1+Lag2,data=Smarket,family=binomial,subset=train)
> glm.probs=predict(glm.fits,Smarket.2005,type="response")
> glm.pred=rep("Down",252)
> glm.pred[glm.probs>.5]="Up"
> table(glm.pred,Direction.2005)Direction.2005
glm.pred Down UpDown 35 35Up 76 106
> mean(glm.pred==Direction.2005)
[1] 0.5595238
> 106/(106+76)
[1] 0.5824176
> predict(glm.fits,newdata=data.frame(Lag1=c(1.2,1.5),Lag2=c(1.1,-0.8)),type="response")1 2
0.4791462 0.4960939


Windows Azure的7月更新:SQL数据库,流量管理,自动缩放,虚拟机)

)



)



)

)




