Educational Codeforces Round 104 (Rated for Div. 2)

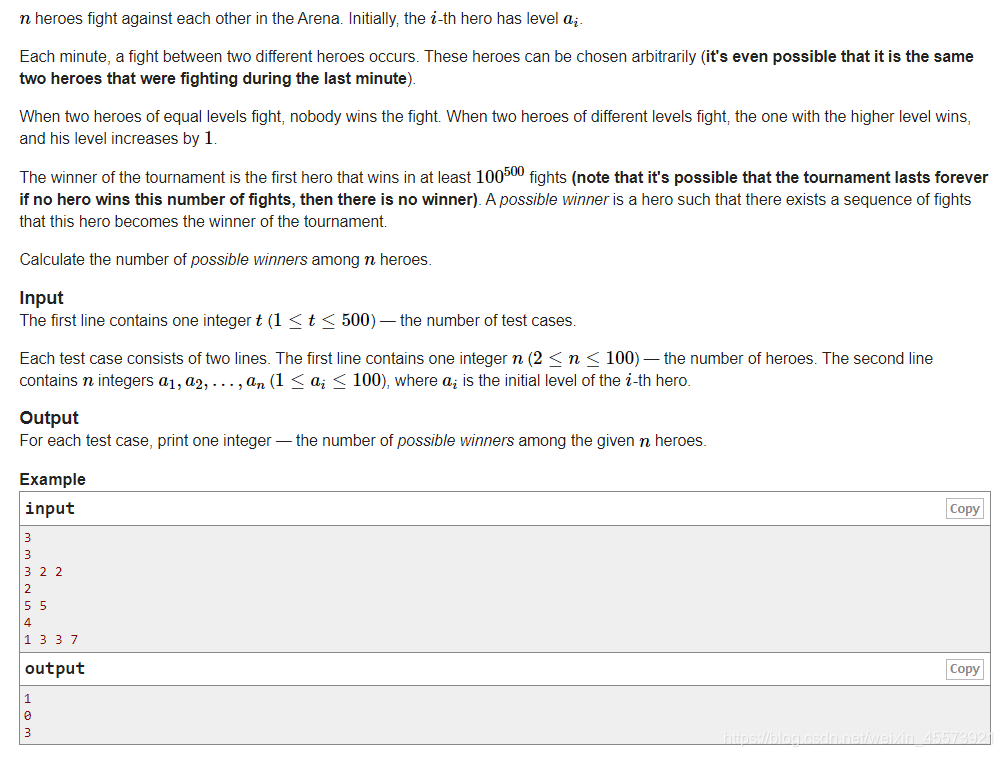
A. Arena

\quad原题链接

http://codeforces.com/contest/1487/problem/A

\quad解题思路

首先，我们看战斗次数是无限的，任意非最小值的英雄都有赢得次数，既然有场次可以赢，那么我们就可以给他安排连胜的序列，是可以成为最后的 winnner 的。因此最终结果为 $n-cnt(min)$总英雄数量减去最小值的次数。

\quadAC代码

#include <bits/stdc++.h>
using namespace std;const int N = 1010, INF = 0x3f3f3f3f;
int a[N], n;int main()
{int t;  cin >> t;while (t -- ){cin >> n;int minblood = INF, cnt = 0;for (int i = 1; i <= n; i ++ )scanf("%d", &a[i]), minblood = min(minblood, a[i]);for (int i = 1; i <= n; i ++ )if (a[i] == minblood)cnt ++;cout << n - cnt << endl;}return 0;
}

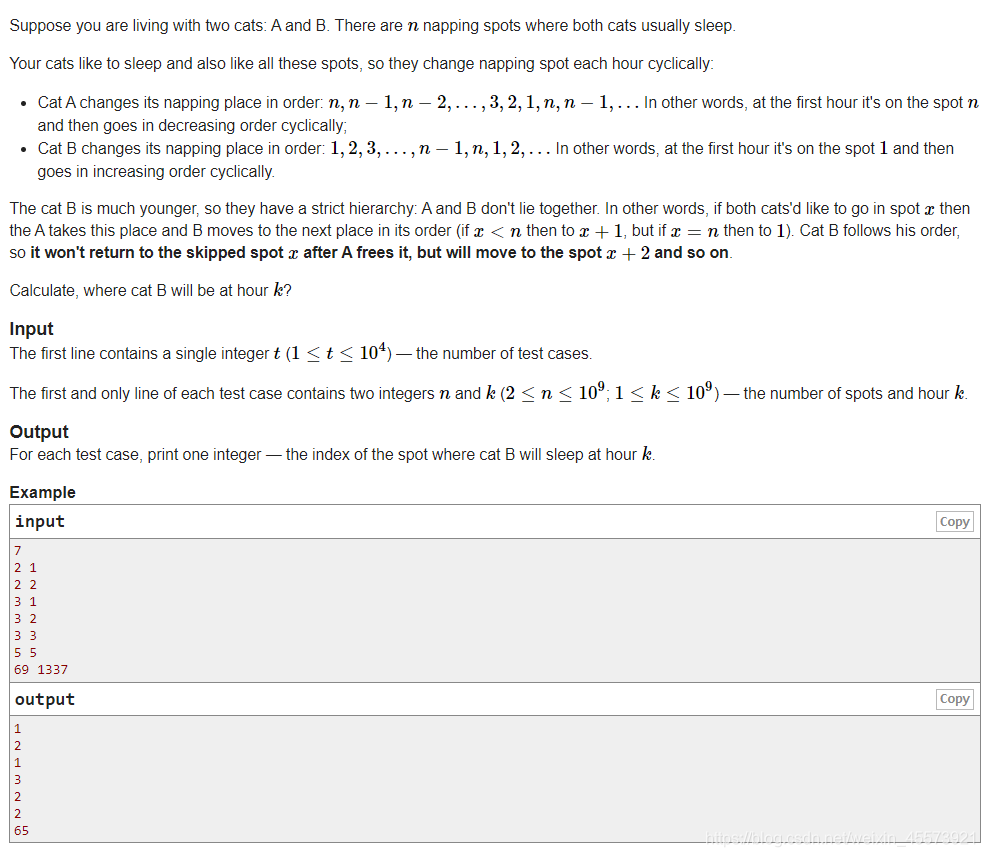
B.Cat Cycle

\quad原题链接

http://codeforces.com/contest/1487/problem/B

\quad解题思路

一种很简单的思路

• 当 n 为偶数时，是不会相撞的，结果很好求

• 那么当$n=2\cdot i+1$为奇数的时候，刚刚开始$B=1,A=2\cdot i+1$，经过$i$步骤达到$B=i+1,A=i+1⟹B=i+2,A=i+1$，也就是说会 经过$i$布相撞，而且相撞后之后两者是刚好错开，距离仍旧是$\lfloor \frac{n-1}{2}\rfloor$，下面我们给出证明：
  假设$A=cur,B=cur+1$，即$B、A$刚好发生冲突，那么我们证明下一次相撞会在什么时刻。
  若首先，倘若两者会相撞，那么要么A减到0，转变成n，要么B增加到了n + 1，变成了1，这样才会有相碰的机会。我们首先计算出 A循环需要的次数为cur - x = 0, x = cur次，B需要的次数为 cur + 1 + x = n + 1, x = n - cur 次。
  若$cur\le n-cur$，那么是 A 会由0转换成 n，然后有一次冲突，设冲突在 t 次，那么有
  $cur-t+n=cur+1+t⟹t=\frac{n-1}{2}$
  若$cur>n-cur$，，那么是 B由n+1向转换成 1，然后有一次冲突，设冲突在 t 次，那么有
  $cur-t=cur+1+t-n⟹t=\frac{n-1}{2}$
  综上，冲突每$\frac{n-1}{2}$会发生一次！！

• 因此， 直接冲突就会 + 1，

很狗的模拟简化复杂度思路

• 当 n 为偶数时，是不会相撞的，结果很好求
• 那么当$n=2\cdot i+1$为奇数的时候，不难发现，每经过$n$次，那么B的原始位置会 + 2，即序列为$1,3,5,\cdot \cdot \cdot$，最后到达 $n$，起始点发生冲突，重回$(1,n)$起点，也就是说循环为$n\ast (n-1)/2$，那么循环内部以 $n$ 为大步长，会冲突两次，那么大步长内部，也会有冲突，下面的冲突就需要列式子计算了。
• 这个方法又麻烦，bug还多，坑惨我了

\quadAC代码

思路一代码

#include <bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 1010, INF = 0x3f3f3f3f;
int n, k;int main()
{int t;  cin >> t;while (t -- ){cin >> n >> k;k --;   // 这样的话，起点就是 (1, n)if (n % 2 == 1) // 奇数冲突会 + 1{k = k + k / (n / 2);}int idx = (1 + k) % n;if (idx == 0)   idx = n;printf("%d\n", idx);}return 0;
}

思路二代码

#include <bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 1010, INF = 0x3f3f3f3f;
LL a[N], n, K;void sol(LL n, LL k)
{if (n % 2 == 0) // 偶数{if (k % n == 0)printf("%d\n", n);elseprintf("%d\n", k % n);}else    // 奇数{k -= 1; // 因为要在初始状态LL mod = LL(n) * (n / 2);  // 循环k %= mod;if (k == 0) printf("1\n");else{LL cnt = k / n;    // 小循环k %= n;LL cur = (1 + cnt * 2);    // B编号if (cur > n)cur -= n;if (k == 0) // 次数耗尽printf("%lld\n", cur);else{LL nxt = (n - cur) / 2;    // 下一次相碰需要的步数if (k < nxt)    // 下一次不会碰了{cur += k;if (cur > n)cur -= n;printf("%lld\n", cur);}else{k -= nxt;cur = cur + nxt + 1;if (cur > n)cur -= n;// 当前的位置是 cur, n - nxt, 还剩下 k 步骤LL A = n - nxt;LL B = cur;if (k == 0){printf("%lld\n", B);return;}A = A - k;B = B + k;if (B <= n) // 还没走出去{printf("%lld\n", B);}else{B -= n;if (B >= A){B ++;}if (B > n)  B -= n;printf("%lld\n", B);}}}}}
}
int main()
{int t;  cin >> t;while (t -- ){cin >> n >> K;// printf("ans=\n\t");sol(n, K);}return 0;
}

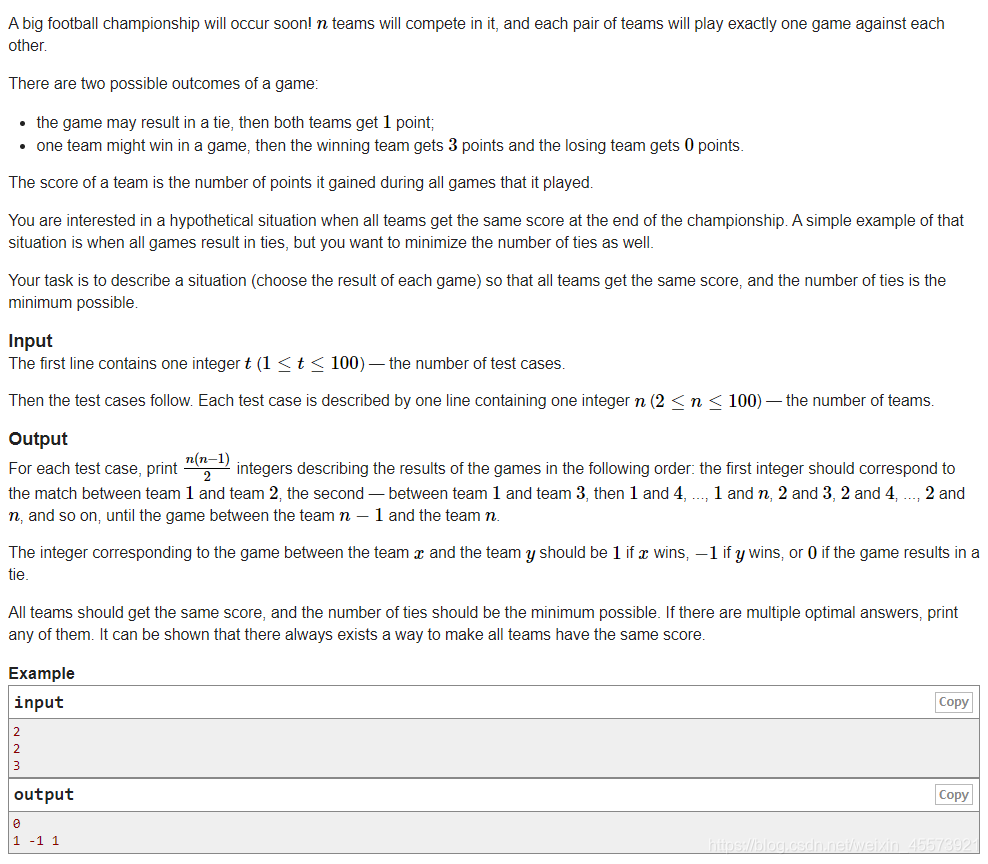
C.Minimum Ties

\quad原题链接

http://codeforces.com/contest/1487/problem/C

\quad解题思路

本题就是一个比较简单的模拟题，倘若 $n$ 为奇数，那么他对战的球队数量 $n-1$为偶数，那么是可以一半输，一半赢的，关键是如何找到这种方案。首先要想找的话，利用所有球队共有的性质，就可以完成每个队伍的输赢一半。
我们假设球队的数量为$n$，编号为$1,2,3,\cdot \cdot \cdot ,n$，那么我们可以让他们围成一个圈，如下图所示。

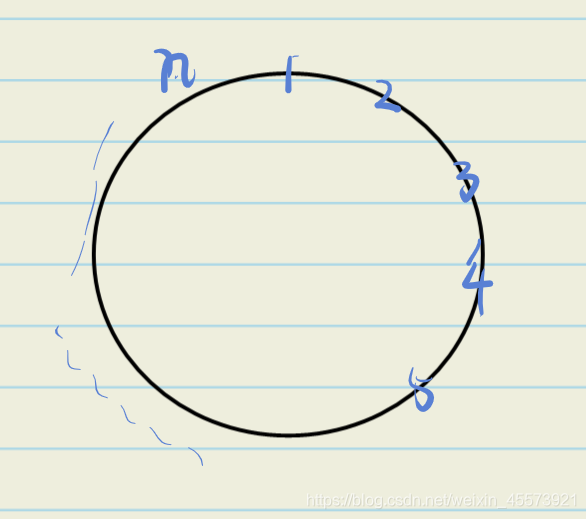
让当前编号i,输给比他编号大的，赢编号比他小的，那么这样就完成了无矛盾的轮转对称。
同理，奇数的时候，也是这样，不过中位数那个编号是平局。

\quadAC代码

#include <bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 1010, INF = 0x3f3f3f3f;
int n, a[N][N];int main()
{int t;  cin >> t;while (t -- ){cin >> n;static int cnt = 0;cnt = n - 1;    // 每支队伍比赛次数for (int i = 1; i < n; i ++ )   // 遍历队伍{if (cnt % 2 == 0)   // 一般赢，一半输{for (int j = 1; j <= n - i; j ++ ){if (j <= cnt / 2){printf("%d ", 1);}else{printf("%d ", -1);}}}else{int tie = (cnt + 1) / 2;for (int j = 1; j <= n - i; j ++ ){if (j < tie){printf("%d ", 1);}else if (j == tie){printf("%d ", 0);}else{printf("%d ", -1);}}}}cout << endl;}return 0;
}

D.Pythagorean Triples

\quad原题链接

http://codeforces.com/contest/1487/problem/D

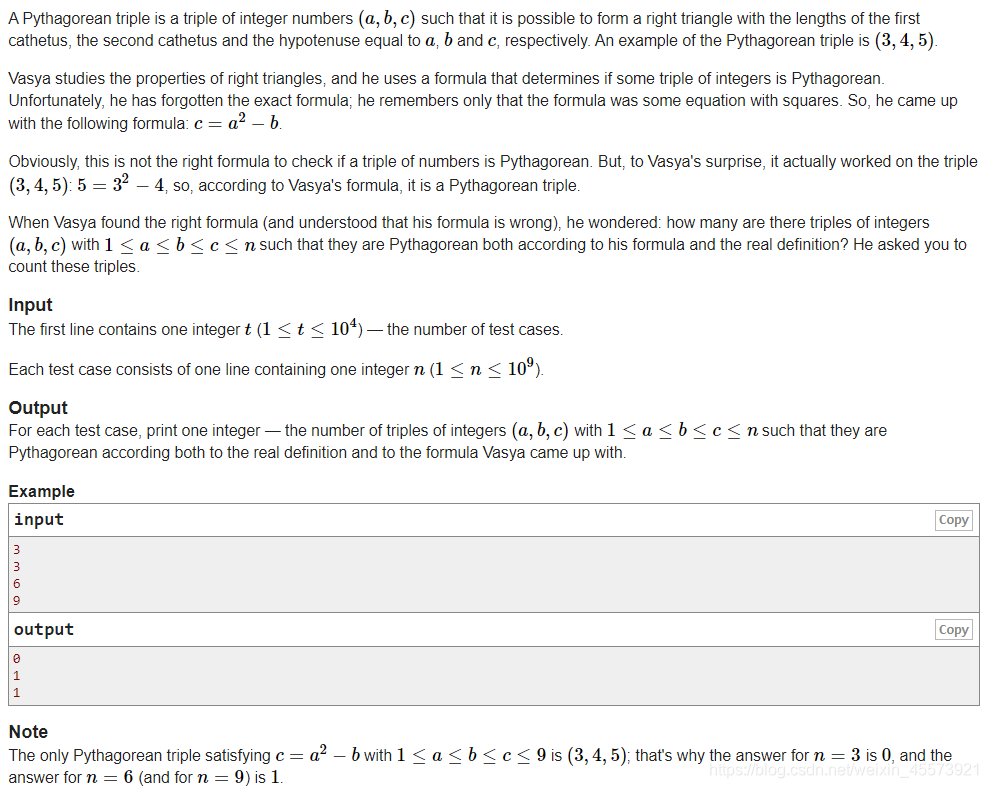
\quad解题思路

就是一个简单的公式推导，最后可以使用二分log(n)，也可以直接O(1)来写sqrt

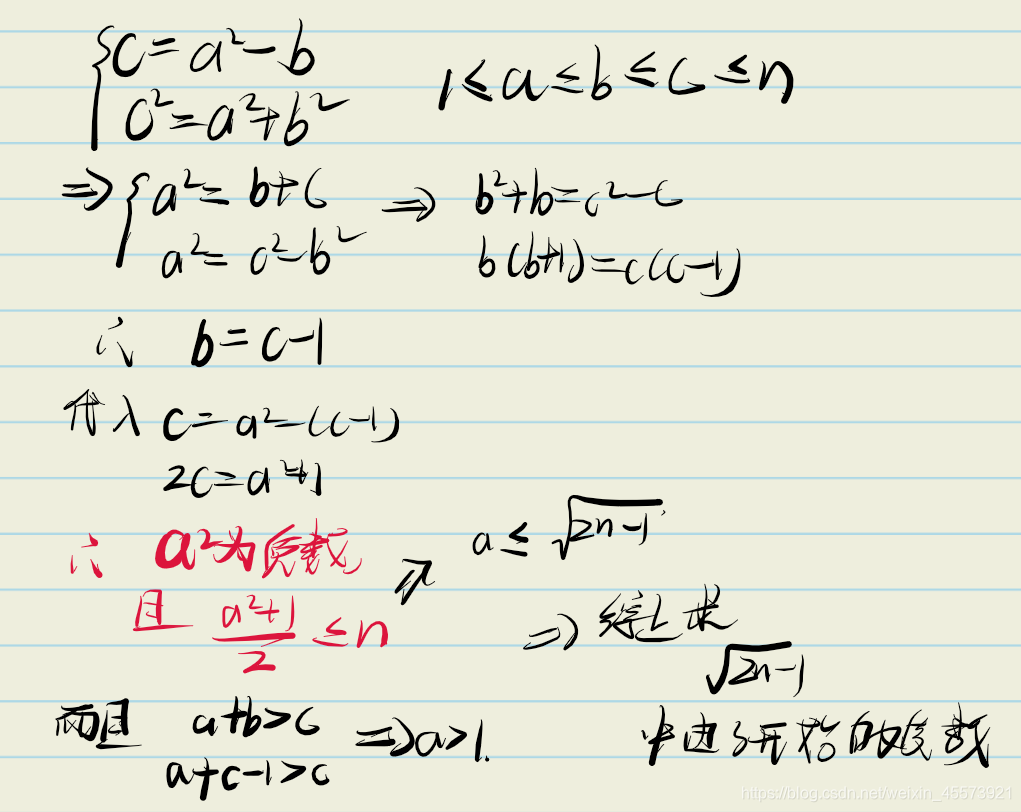
\quadAC代码

#include <bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 1010, INF = 0x3f3f3f3f;
int n, a[N][N];int main()
{int t;  cin >> t;while (t -- ){static int tmp;cin >> n;// printf("Floor:");tmp = floor(sqrt(2 * n - 1));if (tmp % 2 == 0)   tmp -= 1;tmp = tmp / 2;cout << tmp << endl;}return 0;
}

E.Cheap Dinner

\quad原题链接

http://codeforces.com/contest/1487/problem/E

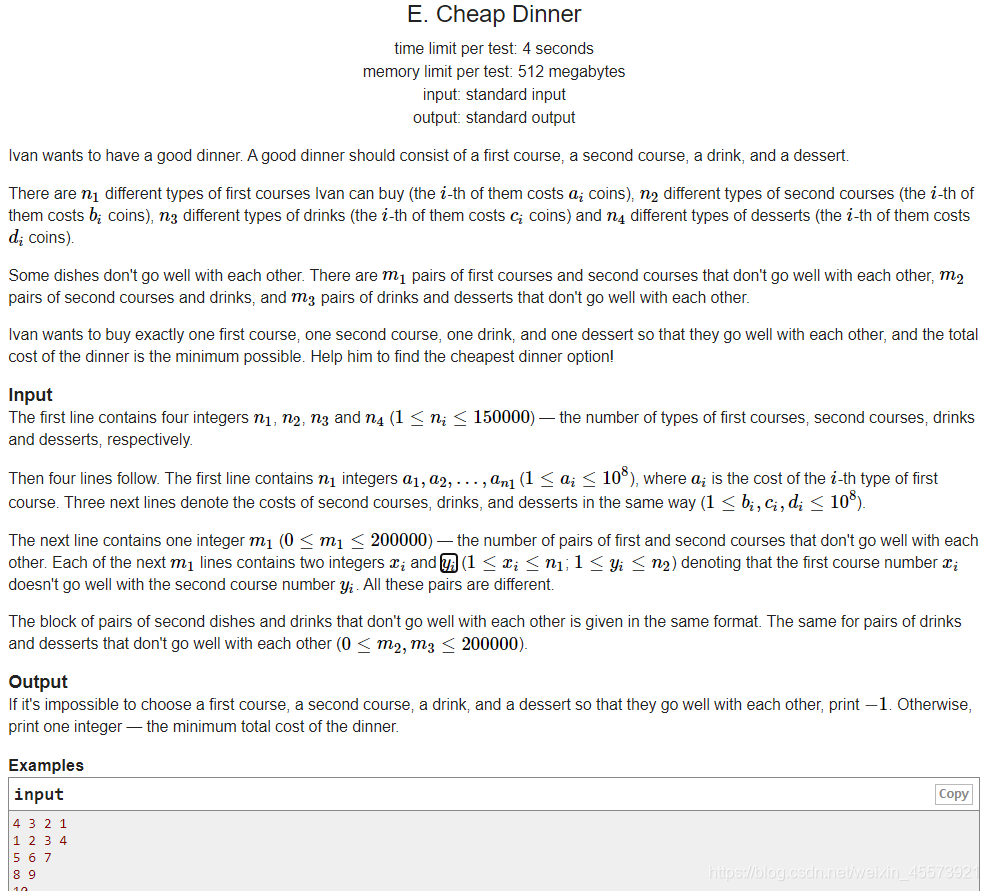
\quad解题思路

分层图 + 贪心进行求解。
对于a, b, c, d四个数组，首先我们用a数组更新b数组，再拿更新之后的b数组更新c数组，一定到d数组，进行结果输出。
关键在于如何进行相邻数组的更新，下面我们以a数组更新b数组为例进行叙述：
利用堆的性质进行贪心更新，首先将 a 的数值存入堆中，假设如今待更新的集合组为 set，那么我们将set中与当前下标冲突的取出，然后更新集合中的剩余数，并将集合清空，再讲原本冲突未更新的点放入，直到堆为空或者是b数组所有元素贪心更新完毕。
关键点是使用STL中的set来降低复杂度

\quadAC代码

#include <bits/stdc++.h>
using namespace std;typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
const int N = 150010, M = 200010;
int a[N], b[N], c[N], d[N];
int n1, n2, n3, n4;
bool st[N];
int h[N], ne[M], e[M], idx;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++;
}// 处理当前这一层
void deal(int a[], int b[], int n1, int n2)
{// initialpriority_queue<PII, vector<PII>, greater<PII> > pque;for (int i = 1; i <= n1; i ++ )if (st[i])pque.push(PII(a[i], i));// inputint m;  cin >> m;memset(h, -1, sizeof h);    idx = 0;for (int i = 1, x, y; i <= m; i ++ ){scanf("%d%d", &x, &y);add(x, y);}//memset(st, false, sizeof st);int surp = n2;PII cur;    int val, idx, u;set<int> s1;    set<int>::iterator it;for (int i = 1; i <= n2; i ++ )s1.insert(i);while (surp != 0 && pque.size()){cur = pque.top();   pque.pop();val = cur.first, idx = cur.second;for (int i = h[idx]; ~i; i = ne[i]){u = e[i];if (!st[u])s1.erase(u);}for (it = s1.begin(); it != s1.end(); it ++ )   // 主要是利用集合来去掉不合适的部分{static int v;   v = * it;b[v] = a[idx] + b[v];st[v] = true;surp --;}s1.clear();for (int i = h[idx]; ~i; i = ne[i]){u = e[i];if (!st[u])s1.insert(u);}}
}int main()
{// inputcin >> n1 >> n2 >> n3 >> n4;for (int i = 1; i <= n1; i ++ )scanf("%d", &a[i]);for (int i = 1; i <= n2; i ++ )scanf("%d", &b[i]);for (int i = 1; i <= n3; i ++ )scanf("%d", &c[i]);for (int i = 1; i <= n4; i ++ )scanf("%d", &d[i]);// 分层图按层次进行for (int i = 1; i <= n1; i ++ )st[i] = true;deal(a, b, n1, n2);deal(b, c, n2, n3);deal(c, d, n3, n4);// 结果输出int res = INF;for (int i = 1; i <= n4; i ++ )if (st[i])res = min(res, d[i]);if (res == INF) res = -1;cout << res << endl;return 0;
}