LeetCode 1824. 最少侧跳次数（DP）

文章目录

- 1. 题目
- 2. 解题

1. 题目

给你一个长度为 n 的 3 跑道道路，它总共包含 n + 1 个点，编号为 0 到 n 。
一只青蛙从 0 号点第二条跑道出发，它想要跳到点 n 处。然而道路上可能有一些障碍。

给你一个长度为 n + 1 的数组 obstacles ，其中 obstacles[i] （取值范围从 0 到 3）表示在点 i 处的 obstacles[i] 跑道上有一个障碍。
如果 obstacles[i] == 0 ，那么点 i 处没有障碍。
任何一个点的三条跑道中 最多有一个 障碍。

比方说，如果 obstacles[2] == 1 ，那么说明在点 2 处跑道 1 有障碍。

这只青蛙从点 i 跳到点 i + 1 且跑道不变的前提是点 i + 1 的同一跑道上没有障碍。
为了躲避障碍，这只青蛙也可以在同一个点处侧跳到另外一条跑道（这两条跑道可以不相邻），但前提是跳过去的跑道该点处没有障碍。

比方说，这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。
这只青蛙从点 0 处跑道 2 出发，并想到达点 n 处的任一跑道，请你返回 最少侧跳次数 。

注意：点 0 处和点 n 处的任一跑道都不会有障碍。

示例 1：
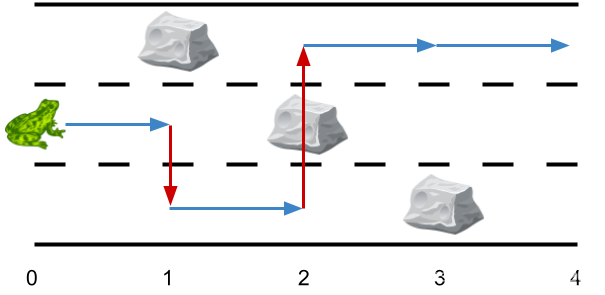
在这里插入图片描述

输入：obstacles = [0,1,2,3,0]
输出：2 
解释：最优方案如上图箭头所示。总共有 2 次侧跳（红色箭头）。
注意，这只青蛙只有当侧跳时才可以跳过障碍（如上图点 2 处所示）。

示例 2：
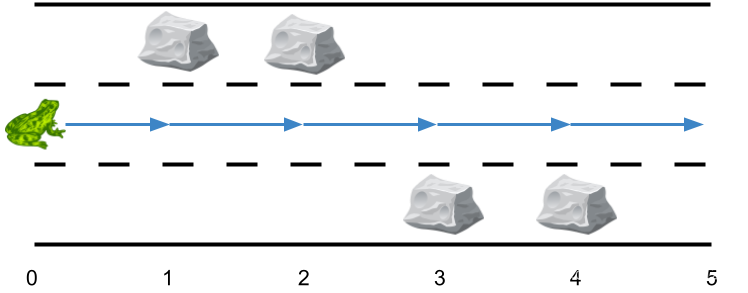
在这里插入图片描述

输入：obstacles = [0,1,1,3,3,0]
输出：0
解释：跑道 2 没有任何障碍，所以不需要任何侧跳。

示例 3：
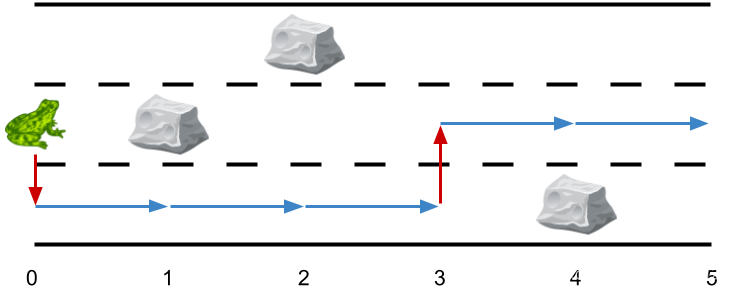
在这里插入图片描述

输入：obstacles = [0,2,1,0,3,0]
输出：2
解释：最优方案如上图所示。总共有 2 次侧跳。提示：
obstacles.length == n + 1
1 <= n <= 5 * 10^5
0 <= obstacles[i] <= 3
obstacles[0] == obstacles[n] == 0

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-sideway-jumps
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

dp[pos][道的编号1-3] 表示到pos位置处在第几号道上的最少侧跳次数

class Solution {
public:int minSideJumps(vector<int>& obstacles) {int n = obstacles.size();vector<vector<int>> dp(n, vector<int>(4, INT_MAX));// dp[pos][道的编号1-3] 表示到pos位置处在第几号道上的最少侧跳次数dp[0][1] = dp[0][3] = 1;dp[0][2] = 0;//初始条件for(int i = 1; i < n; ++i){int prev = obstacles[i-1];//前一位置障碍道编号int cur = obstacles[i];//当前位置障碍道编号for(int j = 1; j <= 3; ++j){if(prev && prev==j)continue;//是障碍，j 不能状态转移for(int k = 1; k <= 3; ++k){if(cur && cur==k)continue;//是障碍不能转移到 kif(j == k)//相同道次dp[i][k] = min(dp[i][k], dp[i-1][j]);else if(prev==k && cur==j)//不同道次，且需要跳两次才能 j -> kdp[i][k] = min(dp[i][k], dp[i-1][j]+2);else//不同道次，只需跳一次dp[i][k] = min(dp[i][k], dp[i-1][j]+1);}}}return min(dp[n-1][1], min(dp[n-1][2], dp[n-1][3]));}
};

760 ms 267.3 MB C++

当前状态只跟上一状态有关，状态可以压缩

class Solution {
public:int minSideJumps(vector<int>& obstacles) {int n = obstacles.size();vector<int> dp(4), tmp(4);dp[1] = dp[3] = 1;dp[2] = 0;//初始条件for(int i = 1; i < n; ++i){tmp[1]=tmp[2]=tmp[3]=INT_MAX;int prev = obstacles[i-1];//前一位置障碍道编号int cur = obstacles[i];//当前位置障碍道编号for(int j = 1; j <= 3; ++j){if(prev && prev==j)continue;//是障碍，j 不能状态转移for(int k = 1; k <= 3; ++k){if(cur && cur==k)continue;//是障碍不能转移到 kif(j == k)//相同道次tmp[k] = min(tmp[k], dp[j]);else if(prev==k && cur==j)//不同道次，且需要跳两次才能 j -> ktmp[k] = min(tmp[k], dp[j]+2);else//不同道次，只需跳一次tmp[k] = min(tmp[k], dp[j]+1);}}swap(dp, tmp);}return min(dp[1], min(dp[2], dp[3]));}
};