1. 题目

给你两个整数数组 nums1 和 nums2 ，它们长度都为 n 。

两个数组的 异或值之和 为 (nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1]) （下标从 0 开始）。

比方说，[1,2,3] 和 [3,2,1] 的 异或值之和 等于 (1 XOR 3) + (2 XOR 2) + (3 XOR 1) = 2 + 0 + 2 = 4 。
请你将 nums2 中的元素重新排列，使得 异或值之和 最小 。

请你返回重新排列之后的 异或值之和 。

示例 1：
输入：nums1 = [1,2], nums2 = [2,3]
输出：2
解释：将 nums2 重新排列得到 [3,2] 。
异或值之和为 (1 XOR 3) + (2 XOR 2) = 2 + 0 = 2 。示例 2：
输入：nums1 = [1,0,3], nums2 = [5,3,4]
输出：8
解释：将 nums2 重新排列得到 [5,4,3] 。
异或值之和为 (1 XOR 5) + (0 XOR 4) + (3 XOR 3) = 4 + 4 + 0 = 8 。提示：
n == nums1.length
n == nums2.length
1 <= n <= 14
0 <= nums1[i], nums2[i] <= 10^7

https://leetcode-cn.com/contest/biweekly-contest-53/problems/minimum-xor-sum-of-two-arrays/
https://leetcode-cn.com/problems/minimum-xor-sum-of-two-arrays/solution/zhuang-tai-ya-suo-dp-by-kobe24o-1h46/

2. 解题

类似题目： LeetCode 1178. 猜字谜（状态压缩+枚举二进制子集+哈希）
第7次 全部通过🚀

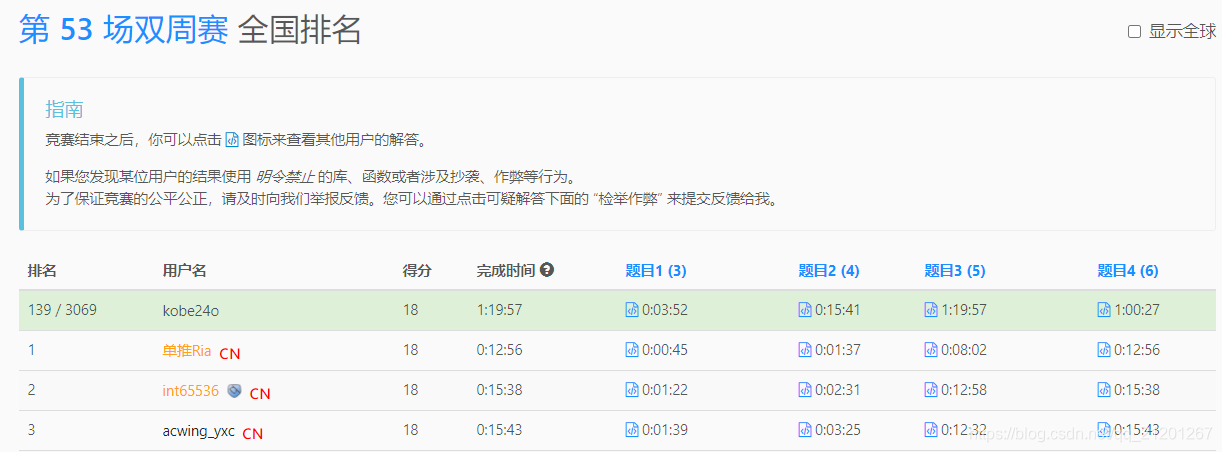
139 / 3069，前 4.53%

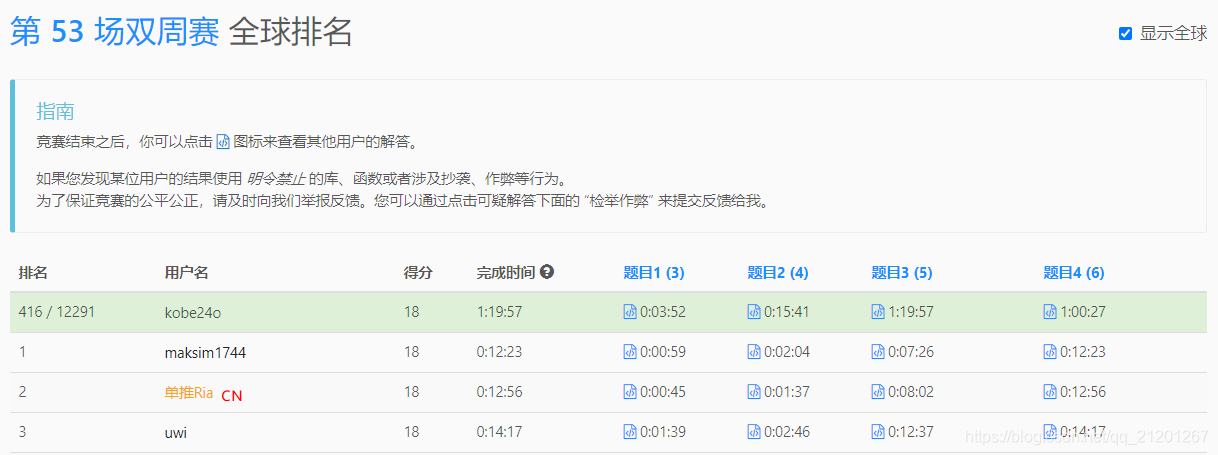
416 / 12291，前 3.38%

2.1 回溯

• 比赛时，写了个回溯，用 n = 14 测了下，会超时

class Solution {int ans = INT_MAX;
public:int minimumXORSum(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();vector<bool> vis(n, false);sort(nums1.rbegin(), nums1.rend());sort(nums2.rbegin(), nums2.rend());dfs(nums1, nums2, vis, 0, 0);return ans;}void dfs(vector<int>& nums1, vector<int>& nums2, vector<bool>& vis, int idx, int XORsum){if(XORsum >= ans)return;if(idx == nums1.size()){if(XORsum < ans)ans = XORsum;return;}for(int i = 0; i < nums2.size(); ++i){if(vis[i]) continue;vis[i] = true;dfs(nums1, nums2, vis, idx+1, XORsum+(nums1[idx]^nums2[i]));vis[i] = false;}}
};

2.2 状态压缩DP

• 用二进制1表示 nums2 各个位置被占用的情况

class Solution {
public:int minimumXORSum(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();vector<int> dp(1<<n, INT_MAX);for(int i = 0; i < n; ++i)dp[1<<i] = nums1[0]^nums2[i];  // 第一个数跟 nums2 结合的情况for(int i = 1; i < n; ++i){	// 剩余的 nums1 的数for(int state = (1<<n)-1; state > 0; --state){	// 遍历所有状态if(dp[state] == INT_MAX) continue; // 不存在的状态，passif(count(state) == i) // 原状态的 1 的个数 为 i 个，可以进行状态转移{for(int j = 0; j < n; ++j){ // 遍历所有的位，碰到 state 0 的位置可以放一个 1if(((state>>j)&1)==0)dp[state|(1<<j)] = min(dp[state|(1<<j)], dp[state]+(nums1[i]^nums2[j]));}}}}return dp.back();}int count(int x){ // 计算 二进制 1 的 个数int s = 0;while(x){s++;x = x&(x-1);}return s;}
};

40 ms 9.1 MB C++

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！