LeetCode 2285. 道路的最大总重要性

文章目录

- 1. 题目
- 2. 解题

1. 题目

给你一个整数 n ，表示一个国家里的城市数目。城市编号为 0 到 n - 1 。

给你一个二维整数数组 roads ，其中 roads[i] = [ai, bi] 表示城市 ai 和 bi 之间有一条双向道路。

你需要给每个城市安排一个从 1 到 n 之间的整数值，且每个值只能被使用一次。
道路的 重要性 定义为这条道路连接的两座城市数值之和。

请你返回在最优安排下，所有道路重要性之和最大为多少。

示例 1：
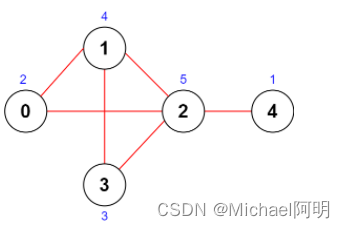
在这里插入图片描述

输入：n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
输出：43
解释：上图展示了国家图和每个城市被安排的值 [2,4,5,3,1] 。
- 道路 (0,1) 重要性为 2 + 4 = 6 。
- 道路 (1,2) 重要性为 4 + 5 = 9 。
- 道路 (2,3) 重要性为 5 + 3 = 8 。
- 道路 (0,2) 重要性为 2 + 5 = 7 。
- 道路 (1,3) 重要性为 4 + 3 = 7 。
- 道路 (2,4) 重要性为 5 + 1 = 6 。
所有道路重要性之和为 6 + 9 + 8 + 7 + 7 + 6 = 43 。
可以证明，重要性之和不可能超过 43 。

示例 2：
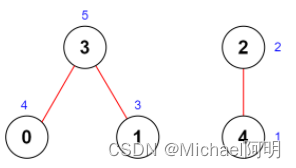
在这里插入图片描述

输入：n = 5, roads = [[0,3],[2,4],[1,3]]
输出：20
解释：上图展示了国家图和每个城市被安排的值 [4,3,2,5,1] 。
- 道路 (0,3) 重要性为 4 + 5 = 9 。
- 道路 (2,4) 重要性为 2 + 1 = 3 。
- 道路 (1,3) 重要性为 3 + 5 = 8 。
所有道路重要性之和为 9 + 3 + 8 = 20 。
可以证明，重要性之和不可能超过 20 。提示：
2 <= n <= 5 * 10^4
1 <= roads.length <= 5 * 10^4
roads[i].length == 2
0 <= ai, bi <= n - 1
ai != bi
没有重复道路。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximum-total-importance-of-roads
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

记录所有的节点的连接的边的次数，排序
贪心：次数大的，安排大的数字，

class Solution {
public:long long maximumImportance(int n, vector<vector<int>>& roads) {vector<int> ct(n);for(auto& r : roads){ct[r[0]]++, ct[r[1]]++;}sort(ct.begin(), ct.end());long long ans = 0;for(int i = 1; i <=n; ++i)ans += 1LL*i*ct[i-1];return ans;}
};