1. 题目

给你一个二维整数数组 circles ，其中 circles[i] = [xi, yi, ri] 表示网格上圆心为 (xi, yi) 且半径为 ri 的第 i 个圆，返回出现在 至少一个 圆内的 格点数目 。

注意：
格点 是指整数坐标对应的点。
圆周上的点 也被视为出现在圆内的点。

示例 1：

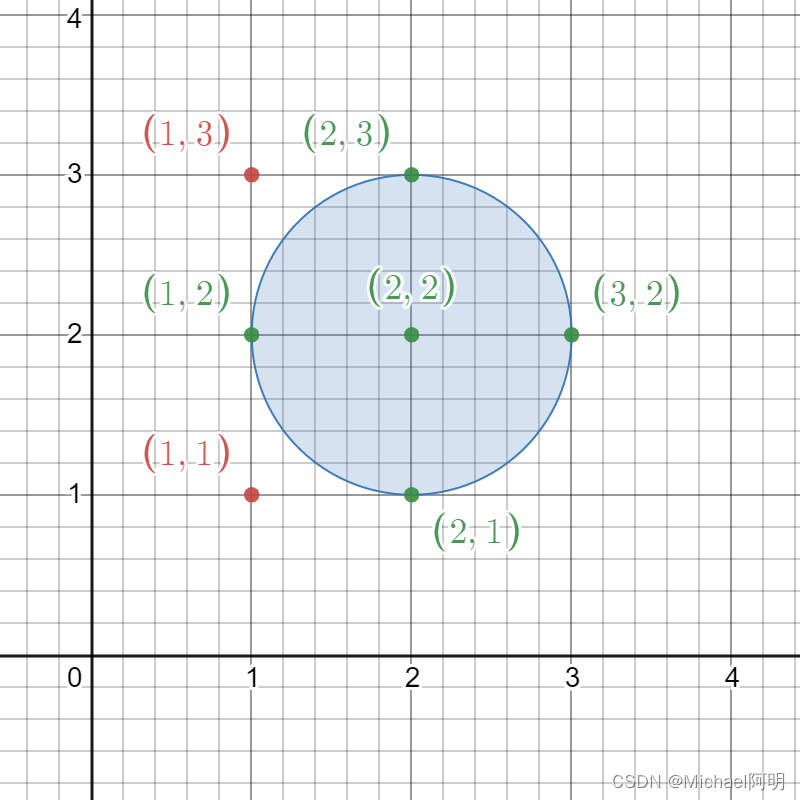
输入：circles = [[2,2,1]]
输出：5
解释：
给定的圆如上图所示。
出现在圆内的格点为 (1, 2)、(2, 1)、(2, 2)、(2, 3) 和 (3, 2)，在图中用绿色标识。
像 (1, 1) 和 (1, 3) 这样用红色标识的点，并未出现在圆内。
因此，出现在至少一个圆内的格点数目是 5 。

示例 2：

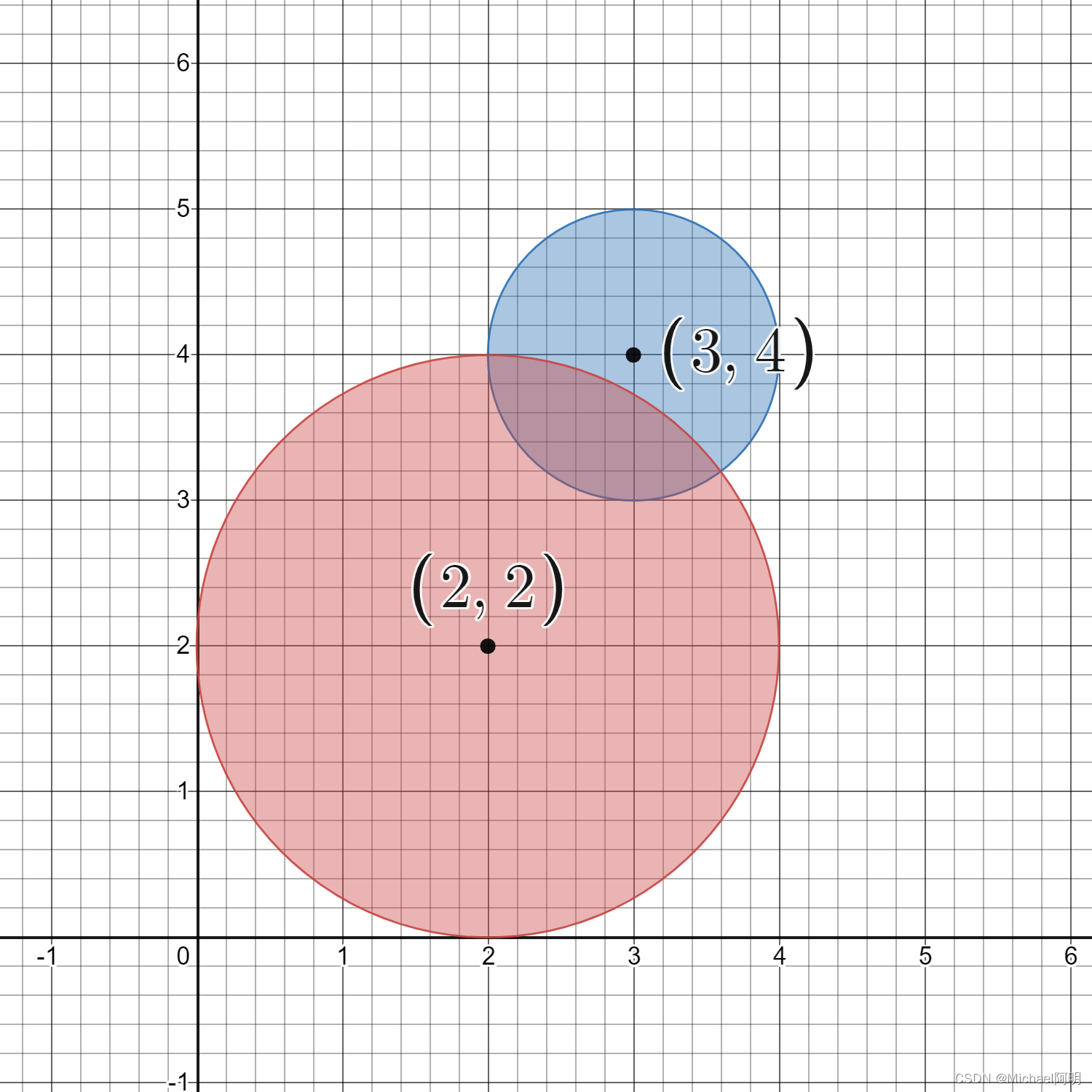
输入：circles = [[2,2,2],[3,4,1]]
输出：16
解释：
给定的圆如上图所示。
共有 16 个格点出现在至少一个圆内。
其中部分点的坐标是 (0, 2)、(2, 0)、(2, 4)、(3, 2) 和 (4, 4) 。提示：
1 <= circles.length <= 200
circles[i].length == 3
1 <= xi, yi <= 100
1 <= ri <= min(xi, yi)

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/count-lattice-points-inside-a-circle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

class Solution:def countLatticePoints(self, circles: List[List[int]]) -> int:X = max(x+r for x,y,r in circles) # 最大的边界Y = max(y+r for x,y,r in circles) # 最大的边界ans = 0circles.sort(key=lambda x: x[-1], reverse=True) # 半径大的先找for x in range(X+1):for y in range(Y+1):for x0, y0, r in circles:if (x-x0)*(x-x0) + (y-y0)*(y-y0) <= r*r:ans += 1breakreturn ans

872 ms 14.9 MB Python3

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！