文章目录
- 1 为什么需要Alignment
- 2 穷举所有的alignment
- 2.1 HMM的对齐
- 2.2 CTC的对齐
- 2.3 RNN-T的对齐
- 3 小结
本文为李弘毅老师【Speech Recognition - Alignment of HMM, CTC and RNN-T (optional)】的课程笔记,课程视频youtube地址,点这里👈(需翻墙)。
下文中用到的图片均来自于李宏毅老师的PPT,若有侵权,必定删除。
文章索引:
上篇 - 1-4 HMM
下篇 - 1-6 RNN-T Training
总目录
1 为什么需要Alignment
现在所有的seq2seq的模型forward的过程,从宏观上来讲,就是我们输入一个序列XXX,可以输出产生任意序列YYY的概率。
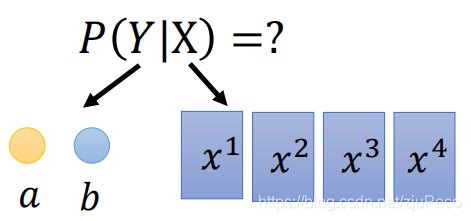
然后decode的时候,我们就是要找到一个序列YYY,使得P(Y∣X)P(Y|X)P(Y∣X)最大。在找这个序列的时候,一般不会穷举,而是通过Beam Search去做。
Decoding:Y∗=argmax⏟YlogP(Y∣X)Decoding:Y^*= \underbrace{argmax}_Y logP(Y|X) Decoding:Y∗=YargmaxlogP(Y∣X)
像LAS这样的的输出中没有额外的符号的模型,其结果就直接是P(Y∣X)P(Y|X)P(Y∣X)了。比如上图要计算输出序列ababab的概率就是
P(Y∣X)=P(a∣X)P(b∣a,X)P(<EOS>∣ab,X)P(Y|X)=P(a|X)P(b|a,X)P(<EOS>|ab,X) P(Y∣X)=P(a∣X)P(b∣a,X)P(<EOS>∣ab,X)
如果有点忘了LAS的decoder是长什么样的话,可以看下面这幅图。
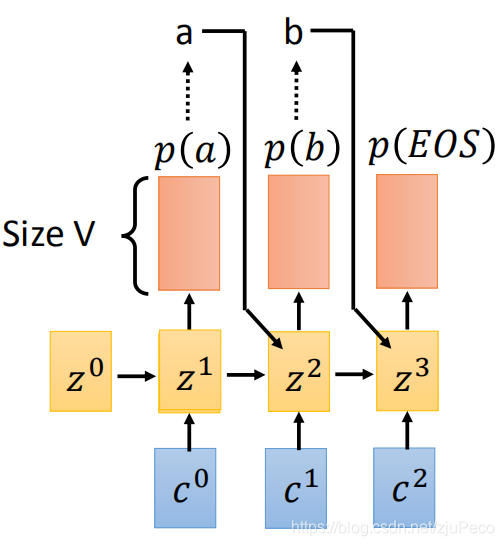
在训练的时候,我们就希望训练出一组模型参数θ\thetaθ下,使得模型在decode的时候,得到标签Y^\hat{Y}Y^的概率是最大的。
Training:argmax⏟θlogPθ(Y^∣X)Training: \underbrace{argmax}_{\theta}logP_{\theta}(\hat{Y}|X) Training:θargmaxlogPθ(Y^∣X)
以上的是模型输出符号都是字典里的字符的情况,但是,当用CTC或者RNN-T这样的模型时,我们的结果中是会出现ϕ\phiϕ这样的占位符的,那么就不能简单地直接计算P(Y∣X)P(Y|X)P(Y∣X)了。而HMM这样的模型,会需要去掉重复的字符,故也不能直接计算。
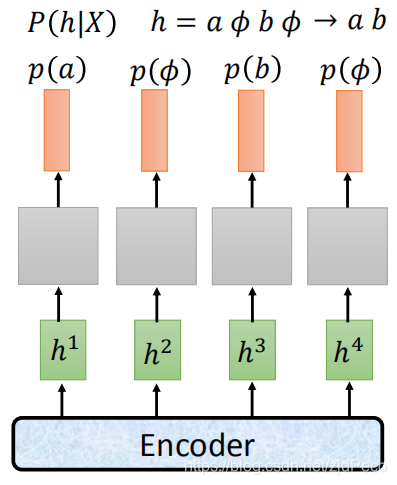
这个时候,我们需要计算的是所有能够通过相应的对齐规则对齐到YYY的输出序列hhh概率之和。
P(Y∣X)=∑h∈align(Y)P(h∣X)P(Y|X) = \sum_{h \in align(Y)}P(h|X) P(Y∣X)=h∈align(Y)∑P(h∣X)
这就是我们要讲alignment的原因。
下文会讲到的如何穷举所有可能的alignment。也就是上面公式中h∈align(Y)h \in align(Y)h∈align(Y)这个集合是怎么来的。
2 穷举所有的alignment
为了方便说明,我们假设现在输入的sequence长度为6,输出的sequence为"cat"。由于HMM,CTC和RNN-T对齐的规则有所不同,故他们在找h∈align(Y)h \in align(Y)h∈align(Y)这个集合的时候,也会有些不同。
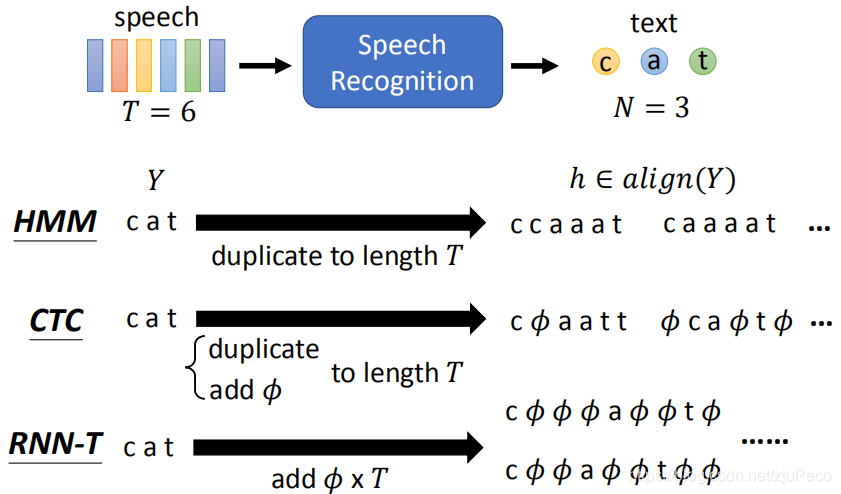
2.1 HMM的对齐
HMM的对齐规则为:
- 去掉所有的相邻重复字符
所以,HMM在找h∈align(Y)h \in align(Y)h∈align(Y)的时候,就是在"cat"的基础上,加入重复的字符,使得序列的长度等于T=6T=6T=6。写成演算法的话,就是下图中灰色方框里这样。比如我们的目标是"cat",那么N=3N=3N=3,然后我们从"c"开始选择重复一次或者多次,接着再去重复"a"和"t",我们需要保证所有的字符都至少出现一次,且它们出现的次数之和为输入序列的长度TTT。
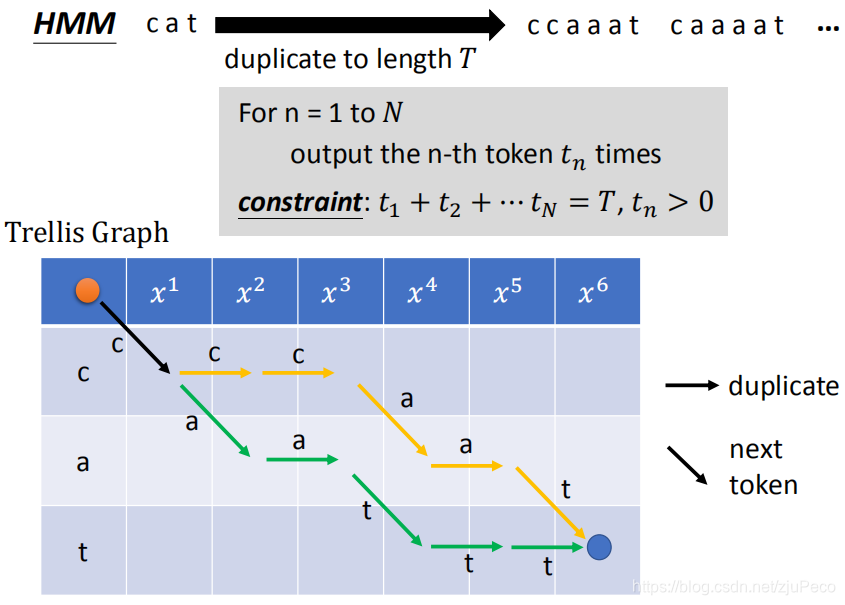
HMM要找的所有alignment都可以画在一个表格当中。这个表格的起点为左上角的橘黄色的点,终点为右下角蓝色的点。往右下方走,表示选择下一个token,往正右方走,表示重复一个token。我们要在保证每次只能往右下或者正右的情况下,从橘点走到蓝点。每一种走法的路径,就是一个alignment。
2.2 CTC的对齐
CTC的对齐规则为:
- 首先合并所有的相邻重复字符
- 然后去除掉所有的ϕ\phiϕ
所以,CTC在找h∈align(Y)h \in align(Y)h∈align(Y)的时候,就是在"cat"的基础上,加入重复的字符和ϕ\phiϕ,使得序列的长度等于T=6T=6T=6。写成演算法的话,就是下图中灰色方框里这样。比如我们的目标是"cat",那么N=3N=3N=3,然后我们从"c"或者“ϕ\phiϕ”开始选择重复一次或者多次,接着再去重复"a","ϕ\phiϕ“和"t”,"ϕ\phiϕ",我们需要保证所有的字符都至少出现一次,"ϕ\phiϕ“可以出现也可不出现,且字符和”ϕ\phiϕ"出现的次数之和为输入序列的长度TTT。
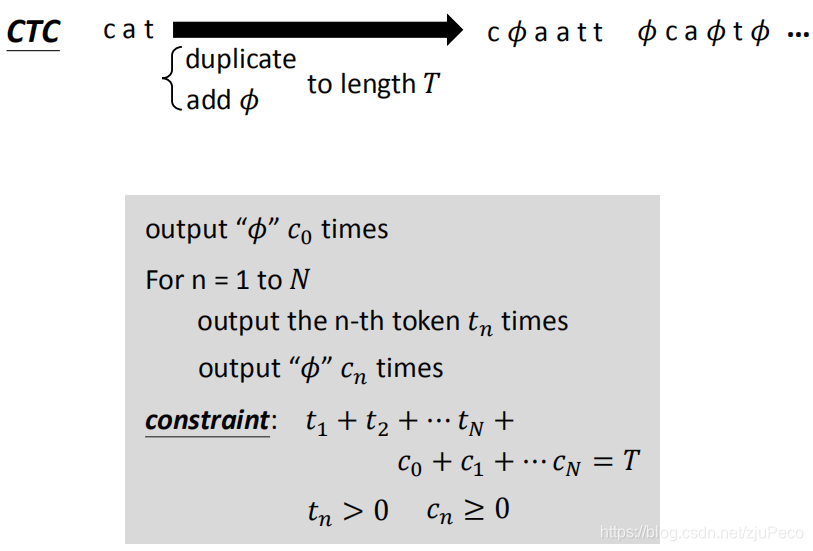
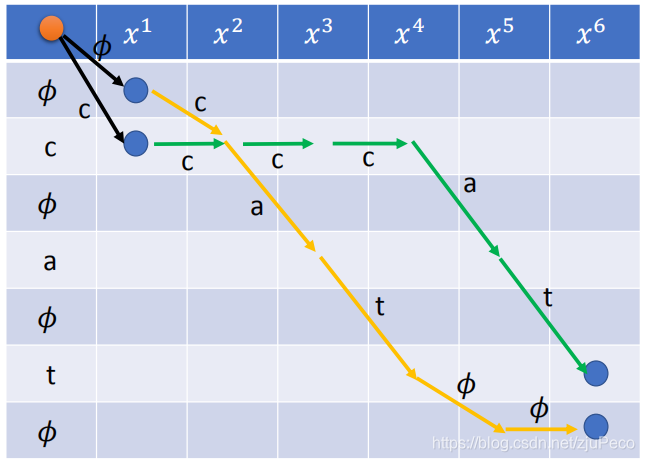
CTC要找的所有alignment同样也可以画在一个表格当中。这个表格的起点为左上角的橘黄色的点,终点有两个,为右下角蓝色的点。
第一步,我们可以选择字符或者“ϕ\phiϕ”;如果选择了字符"c",那么接下来可以有3种选择,分别是往正右重复,往右下对角插入一个"ϕ\phiϕ",往右下走马步插入字符"a"。
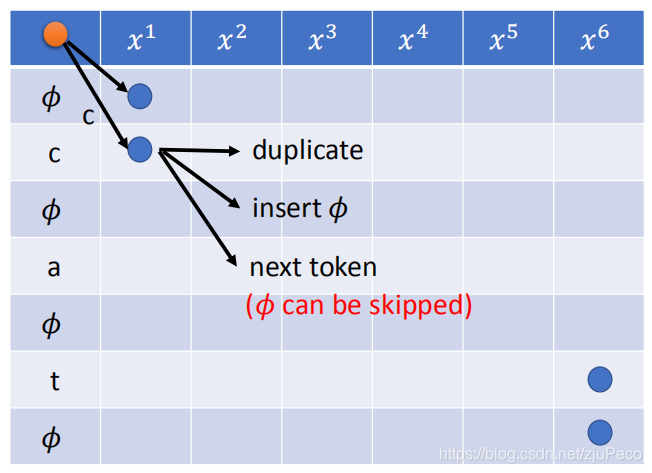
如果我们选择的是"ϕ\phiϕ",那么我们就只有2种选择,分别是往正右重复"ϕ\phiϕ“或者往右下对角插入字符"c”。这个时候,是不能走右下马步重复ϕ\phiϕ的。
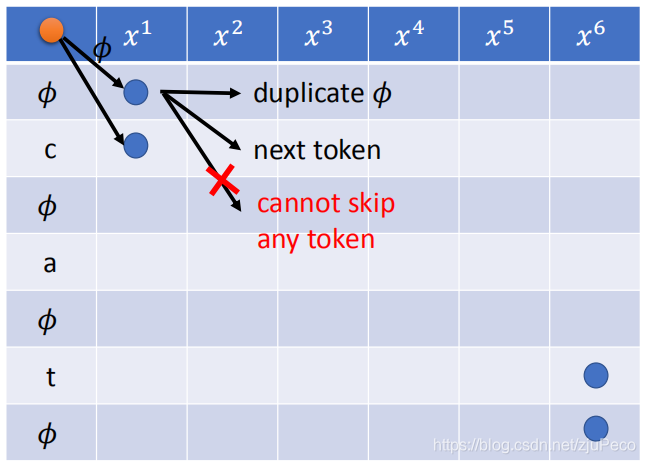
总结一下,就是在"ϕ\phiϕ"行的时候,有正右或者右下对角2种选择,在字符行的时候,有正右或者右下对角或者右下马步3种选择。
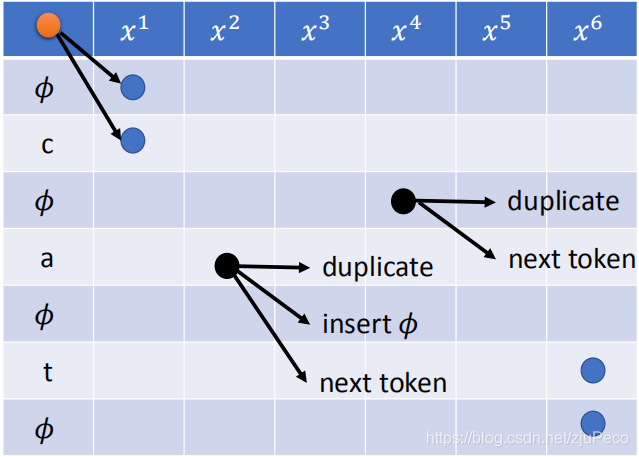
还有一种特殊情况需要注意的是,如果走右下角马步得到的字符和当前字符是相同的时候,不同走右下角马步。

基于以上的这些规则,从橘点走到右下脚两个蓝点中的任意一个所经过的路径都是一个合理的alignment。
2.3 RNN-T的对齐
RNN-T的对齐规则为:
- 去除掉所有的ϕ\phiϕ
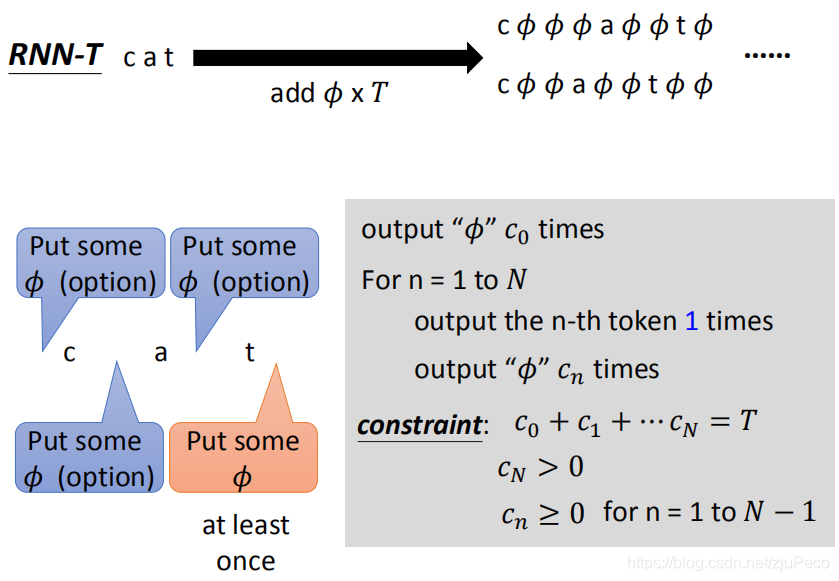
所以,RNN-T在找h∈align(Y)h \in align(Y)h∈align(Y)的时候,就是在"cat"的基础上,加入T=6T=6T=6个ϕ\phiϕ。写成演算法的话,就是下图中灰色方框里这样。我们在每个字符之间都可以插入数量不等的"ϕ\phiϕ",但是末尾至少要有1个"ϕ\phiϕ",然后所有"ϕ\phiϕ“的个数之和为T=6T=6T=6。
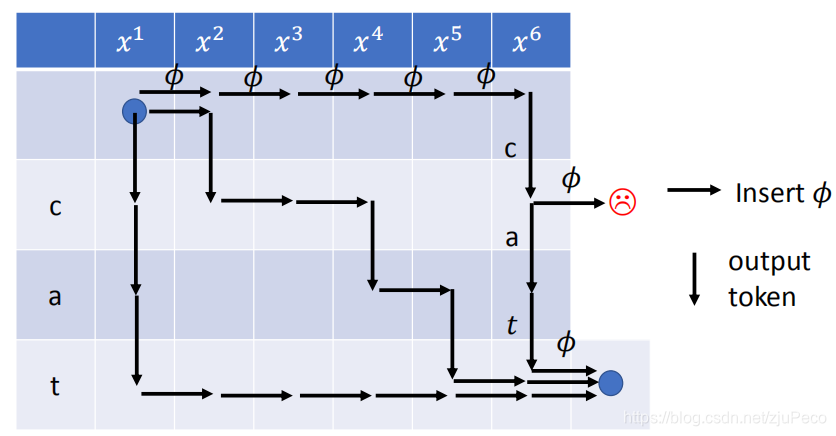
RNN-T要找的所有alignment同样也可以画在一个表格当中,不过这个表格和之前的有所不同。这个表格的起点为左上角的蓝色的点,终点为右下角蓝色的点。每往正右走一步就是插入一个”ϕ\phiϕ",每往正下走一步就是插入一个字符,直到走到右下角的蓝点,所经过的路径都是一个合理的alignment。
3 小结
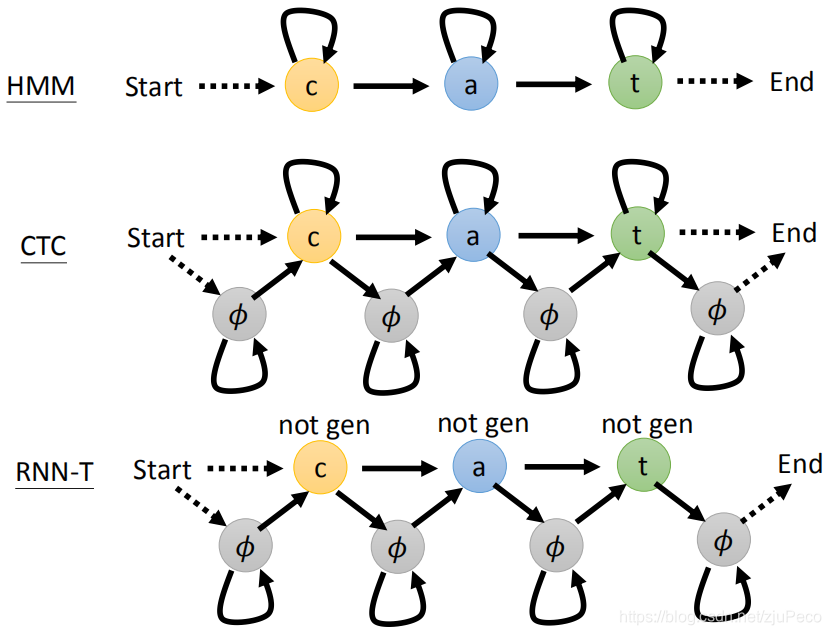
HMM、CTC和RNN-T都可以用如下图所示的HMM专用的状态转移图来表示。其实也就是上文所述的东西,我觉得就算不看下面这个图也无所谓,所以这里就不讲了。



)



)











)