文为李弘毅老师【Transformer】的课程笔记，课程视频youtube地址，点这里👈(需翻墙)。

下文中用到的图片均来自于李宏毅老师的PPT，若有侵权，必定删除。

1 内容简述

抛开Transformer的内部结构，Transformer其实就是一个seq2seq的模型，其中用到了大量的self-attention layer。本文会试图讲明白什么是self-attention layer。

2 seq2seq的常用模块

之前使用最广泛的seq2seq的模块就是RNN。RNN可以分为单向的和双向的。如果是单向的RNN，输出中的每个time step会有一些信息丢失，比如单向的RNN在下图中产生$b^3$的时候就只考虑了$[a^1,a^2,a^3]$。而双向的RNN输出的每个time step都考虑了输入的所有信息，比如双向的RNN在下图中产生$b^3$的时候就考虑了$[a^1,a^2,a^3]$和$[a^3,a^4]$。

但是RNN有一个不好的地方就是它的计算很难并行化，比如我要算$b^4$的时候，就要等前几个结果都出来了，才能算。为了解决这个问题，就有人提出了CNN来替换RNN。

1-D CNN的模块介绍可以参见这里。虽然CNN的计算可以并行处理，但是，CNN的kernel_size一般会比较小，输出的某个time step想要考虑到全局的信息，就要把CNN叠很多层。

然后本文的重点就由此引出了，self-attention可以同时解决这两个问题，也就是既可以让每个time step的输出考虑了全局的输入，又可以并行计算。

左图为RNN，右图为CNN

3 Self-attention

self-attention最早出自google的这篇Attention Is All You Need，这篇文章比较难读懂，但它本身并不是那么神秘，一个非常直观的理解就是，self-attention是一个可以替代RNN的东西。下面就来剖析一下这个self-attention。我们的目的是输入一个序列$a$，得到一个序列$b$。

假设我们的输入是$x$，首先要对$x$进行一次embedding，让它变到我们需要的维度，我们记这个embedding的结果为$a$。

$$a=Wx$$

然后，我们要让这个$a$再分别乘以三个矩阵，self-attention中最为重要的三个东西query, key和value。

$$\begin{gathered} q:query(tomatchothers) \\ q=W^{q}a \\ k:key(tobematched) \\ k=W^{k}a \\ v:value(informationtobeextracted) \\ v=W^{v}a \end{gathered}$$

然后，我们会把每一个q去对k做attention，所谓的attention就是塞两个向量进去，然后吐出来一个表示两个向量相关性的数值$\alpha$。attention的方法有很多种，在Attention Is All You Need中，所使用的叫做scaled dot-product attention。

$${\alpha }_{1,i}=q^1\cdot k^i/\sqrt{d}$$

为什么要除以这个$\sqrt{d}$呢？因为当$q$和$k$的维度很大时，它们内积的variance就会很大，所以要除以一个$\sqrt{d}$来scale一下。

最后还要对$\alpha$做一个softmax，得到$\hat{\alpha }$。大致的流程如下图所示。

这个$\hat{\alpha }$其实就是每一个time step的value的重要性。用这个$\hat{\alpha }$对每个time step的value进行一个加权，就得到了self-attention的结果$b$。比如$b^1$就可以通过下式计算得到
$$b^1=\sum _i{\hat{\alpha }}_{1,i}{v}^i$$

这样得到的$b$是考虑了所有的输入的，而且无视输入之间的远近，完全通过学习attention来获取需要的value，其示意图如下所示。

更重要的是，以上的过程都是可以并行计算的。因为每个time step的计算都是独立的，我们可以把它们concat到一个大的矩阵里，然后一起计算，示意图如下所示。

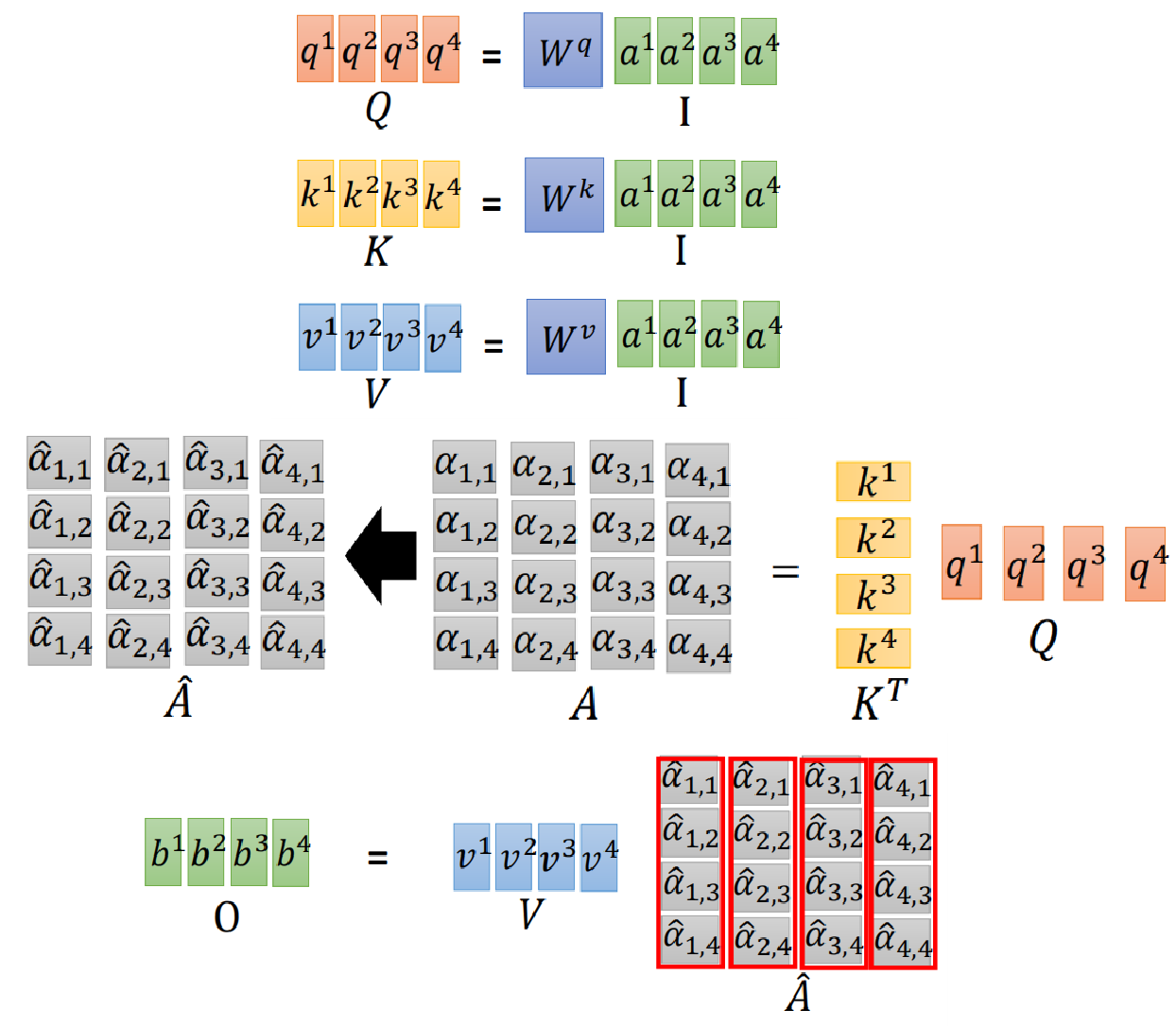
4 Multi-head Self-attention

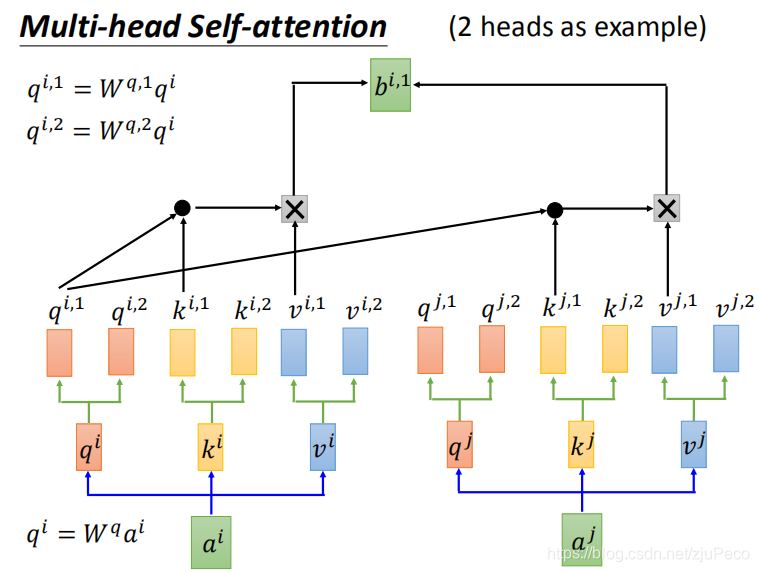
self-attention是可以做成multi-head的，所谓multi-head，其实就是把$q$，$k$，$v$分裂成多个，然后每个分别在自己的head内做self-attention，然后把结果再concat起来，如果得到的结果维度不是我们想要的，那么再乘以一个矩阵就可以了。

做成Multi-head的目的是让不同的head去学到不同的东西，比如有的head学局部的信息，有的head学全局的信息。

5 Positional Encoding

然而，从之前的整个流程可以看出来，self-attention是不会去关心输入的time step顺序的，任何一个输出，time step是$1$还是$T$，对self-attention来说都是一样的，李老师很形象地称之为“天涯若比邻”。

为了增加位置的信息，就会给$a$加上一个神奇的人为预先设定好的向量$e$，有了这个$e$之后，模型就可以知道输入的位置信息了。

那为什么是$e+a$，这样不是把$a$的信息给搅乱了吗？会什么不是直接concat上去变成$[e,a]$呢？我们不妨来试试concat的话会如何，不过既然是位置信息，我们需要concat到$x$上。假设我们有一个和位置有关的向量$p$，$p$是一个one-hot的向量，表示当前的$x^i$是在第$i$个time step上。那么在做embedding的时候，我们也需要把embedding的矩阵$W$变大，而$W$又可以拆成$W^i$和$W^p$。根据矩阵的计算方法，其结果就相当于给$a$加了一个值，这个值也就是之前提到的$e$的。可见，$e+a$和对$x$进行concat是等效的。

这里有一个比较神奇的地方，就是这个$e$是个什么东西，为啥这么灵？换成其他的灵不灵？这就不得而知了。

论文中的position encoding用的是

$$\begin{gathered} P{E}_{(pos,2i)}=sin(pos/10000^{2i/d_{model}}) \\ P{E}_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}}) \end{gathered}$$

这是一个不用学习的参数，作者也试过让模型自己去学，但结果差不多。作者选择这个不用学习的版本是为了让模型可以处理比训练时遇到过的序列更长的序列。

也有人把这个可视化了，可以参见illustrated-transformer。

6 Transformer

从上文中可以看出，self-attention是可以替代RNN的，实际操作中，也就是把RNN替换成self-attention就结束了。

接下来让我们来看看下面这幅经典的Transformer的图，现在看起来应该是亲切了不少。这个图的左半个结构是Encoder，右半个结构是Decoder。把图中的Multi-Head Attention想象成RNN就可以了。Emmm…感觉也不需要额外的说明了。值得注意的是，这里的Masked Multi-Head Attention就是指是对已经产生的序列做attention，比如我们翻译的时候，是塞一个起始符进去，然后一个字一个字生成，直到遇到终止符。

参考资料

[1] 李宏毅-transformer
[2] illustrated-transformer
[3] Attention Is All You Need