问题
昨天晚上,小学6年级的外甥女从数学课外辅导班补习回来,兴冲冲的对家里人说,哎,我发现了一个数学的大bug啊。
你说1/3不是一个无限循环小数0.33333...,那么三个1/3加起来,不就是0.99999...吗?可是我们都知道3*1/3=1。这不就是说

这不就是一个大bug嘛!
看到这里,你是否也认为这是一个bug呢?
答案
这不是数学的bug,因为,0.99999......就是等于1。
这看起来有点违反直觉。但是你要注意到,你这里的0.99999......,不是0.9,也不是0.99,甚至不能说是0.99后面跟了一串很长的9,而应该是0.99后面跟了一串无穷长度的9。
一旦涉及到无穷,就不一样了。
你有可能问,可是,不管后面有多少位9,0.99999......总是和1有一个差距吧!没错,如果你把0.99999......在某一位截断的话,那么这个有限长度的0.99999......,确实和1的差距不为0。
但是‘0.99999......’的长度是无穷的,没有所谓的最后一个数字,所以你不能说‘0.99999......’总是和1有一个差距。
看到这里,我们还是摆出严格的数学证明吧。
证明
数字‘0.99999......’,可以被展开成如下的式子

上式中的每一项,都是某个小数点后面跟了一个9,因此可以写成如下的形式
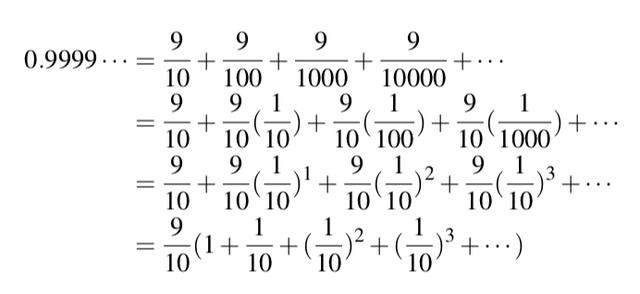
注意到( )内部是一个无限等比数列。按照等比数列的公式,我们可以接着计算

因此,我们证明了0.99999......=1
很多涉及到无穷和极限的东西,都会违反我们的直觉。和上面的例子很相似的一个例子是是古希腊数学家芝诺(Zeno of Elea)提出的一个芝诺悖论。
“一个人从A点走到B点,要先走完路程的1/2,再走完剩下总路程的1/2,再走完剩下的1/2...”如此循环下去,永远不能到终点”。
假设此人速度不变,那么实际需要时间是1/2+1/4+1/8+......。我们知道,虽然这个式子的项有无穷项,但是之和

关于这个的证明,只要从下面的图里看起来就一目了然了。
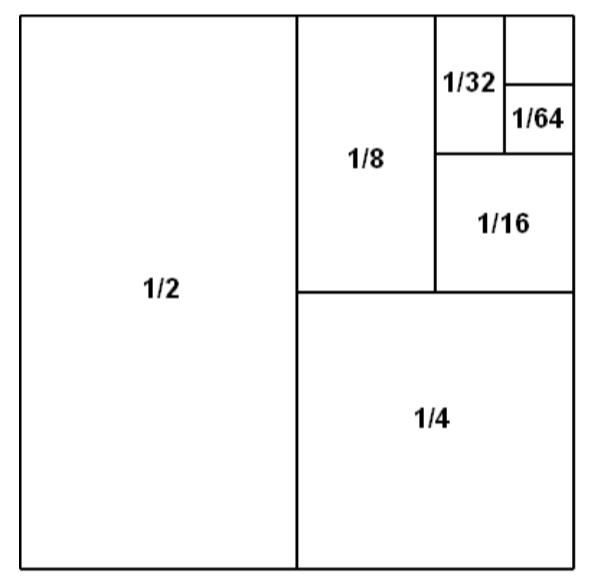
很有意思的是,我们的庄子,在《庄子·天下篇》中直接给出了答案:
“一尺之棰,日取其半,万世不竭”。
庄子的这句话有两点含义(1)“万世不竭”,表明包含有无限的项,(2)"一尺之锤",表明这所有的项之和为1。
今天,我从一个例子,谈起了数学的美妙之处。没有经过数学的训练,我们很多人的思维经常会有很多桎梏,例如很多人无法理解无穷、极限、量级等等,就会导致很多地方出现“违反直觉”的地方。但是经过严格的数学证明,你就可以理解其中的概念了。
好了,今天的就到这里,希望你能有所收获。今天的思考题是,你能不能给出几个违反你的直觉,但是又正确的例子呢?



)



)



)


)


)
)
