红黑树,对很多童鞋来说,是既熟悉又陌生。熟悉是因为在校学习期间,准备面试时,这是重点。然后经过多年的荒废,如今已经忘记的差不多了。如果正在看文章的你,马上快要毕业,面临着找工作的压力;又或者你觉得需要将这块知识重新复习一遍;又或者只是看看,那么恭喜你,赚到了。那么我将带领大家重新认识下红黑树,用简单的语言,搞懂红黑树。
在学习红黑树之前,咱们需要先来理解下二叉查找树(BST)。
要想了解二叉查找树,我们首先看下二叉查找树有哪些特性呢?
1, 左子树上所有的节点的值均小于或等于他的根节点的值
2, 右子数上所有的节点的值均大于或等于他的根节点的值
3, 左右子树也一定分别为二叉排序树
我们来看下图的这棵树,他就是典型的二叉查找树
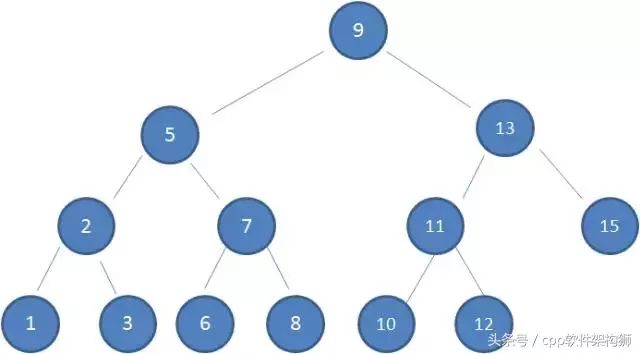
那问题来了,为什么一定要这种结构呢?换句话说这样的结构有什么好处呢?我们就来查找下值为10的节点。它怎么一步步的找到这个节点的?步骤是怎样的?接着往下看。
1, 查找到根节点9,看下图:
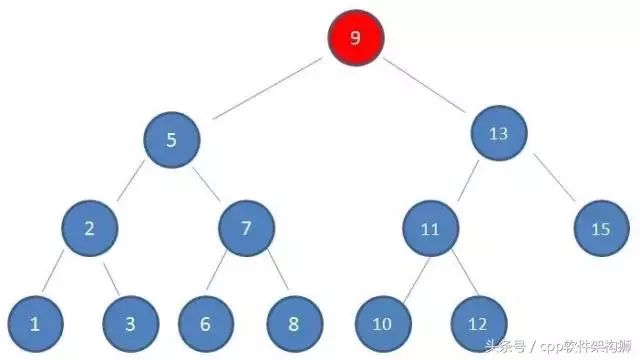
2, 由于10大于9的,所以查找到右孩子13,看下图:
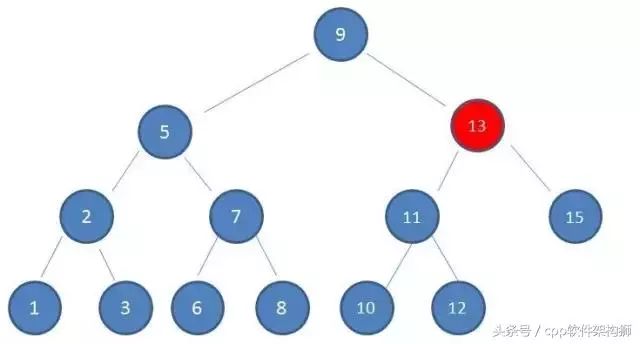
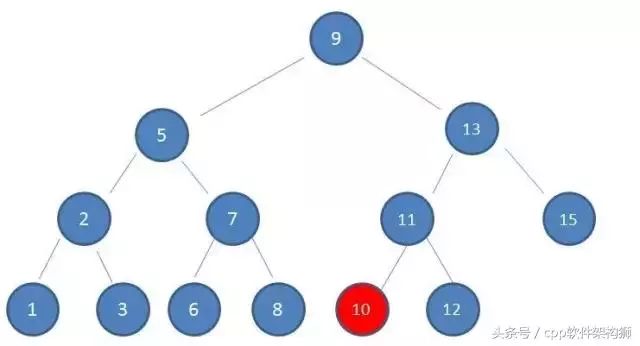
3, 又因为10是小与13的,所以查找到左孩子11,看下图:

4, 这一步相比不用说了大家也都知道了,找到了左孩子,然后发现正好是10 。恰好是正要寻找的值。
可能又有童鞋会问,这不是二分查找的思想吗?确实,查找所需的最大次数等同于二叉查找树的高度。当然在插入节点的时候,也是这种思想,一层一层的找到合适的位置插入。但是二叉查找树有个比较大的缺陷,而且这个缺陷会影响到他的性能。我们先来看下有一种情况的插入操作:
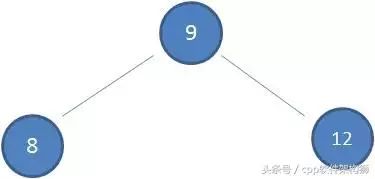
如果初始的二叉查找树只有三个节点,如下图:
我们依次插入5个节点:7,6,5,4,3,。看下图插入之后的图:
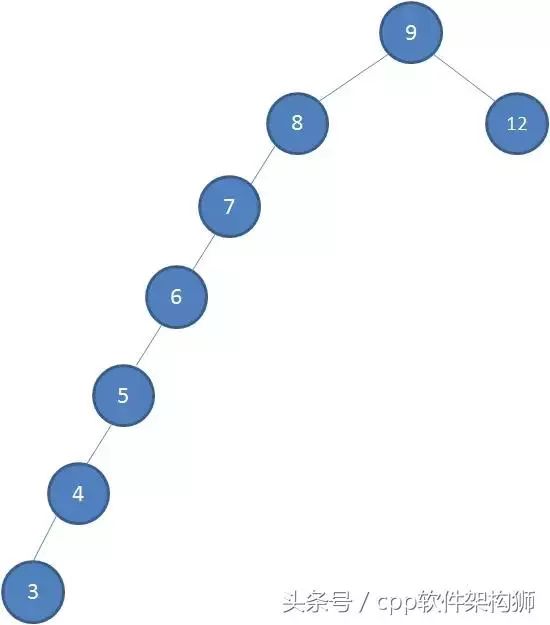
看出来了吗?有没有觉得很别扭,如果根节点足够大,那是不是“左腿”会变的特别长,也就是说查找的性能大打折扣,几乎就是线性查找了。
那有没有好的办法解决这个问题呢?解决这种多次插入新节点而导致的不平衡?这个时候红黑树就登场了。
红黑树就是一种平衡的二叉查找树,说他平衡的意思是他不会变成“瘸子”,左腿特别长或者右腿特别长。除了符合二叉查找树的特性之外,还具体下列的特性:
1. 节点是红色或者黑色
2. 根节点是黑色
3. 每个叶子的节点都是黑色的空节点(NULL)
4. 每个红色节点的两个子节点都是黑色的。
5. 从任意节点到其每个叶子的所有路径都包含相同的黑色节点。
看下图就是一个典型的红黑树: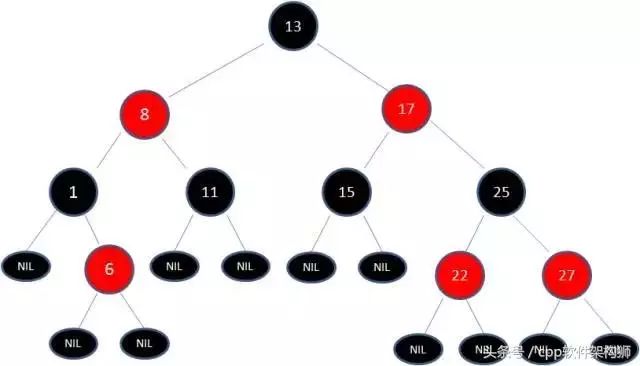
很多童鞋又会惊讶了,天啊这个条条框框也太多了吧。没错,正式因为这些规则,才能保证红黑树的自平衡。最长路径不超过最短路径的2倍。
当插入和删除节点,就会对平衡造成破坏,这时候需要对树进行调整,从而重新达到平衡。那什么情况下会破坏红黑树的规则呢?
1,我们看下图:
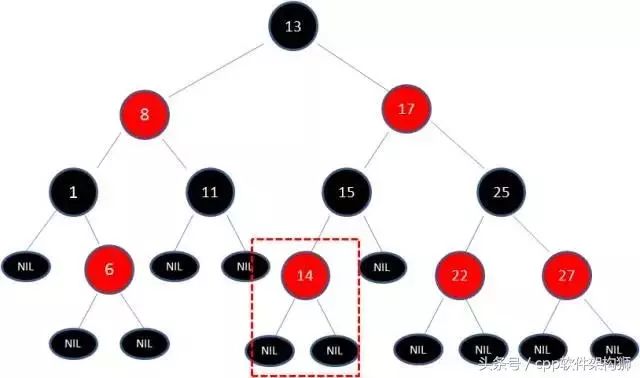
向原来的红黑树插入值为14的新节点,由于父节点15是黑色节点,所以这种情况没有破坏结构,不需要做任何的改变。
2,向原树插入21呢?,看下图:
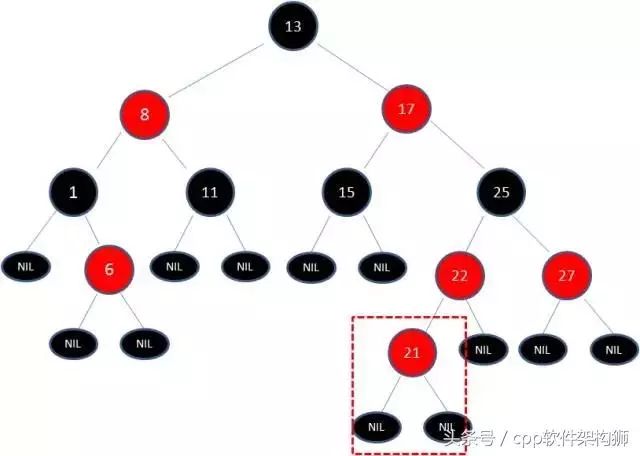
由于父节点22是红色节点,因此这种情况打破了红黑树的规则4,必须作出调整。那么究竟该怎么调整呢?有两种方式【变色】和【旋转】分为【左旋转】和【右旋转】。
【变色】:
为了符合红黑树的规则,会把节点红变黑或者黑变红。下图展示的是红黑树的部分,需要注意节点25并非根节点。因为21和22链接出现红色,不符合规则4,所以把22红变黑:
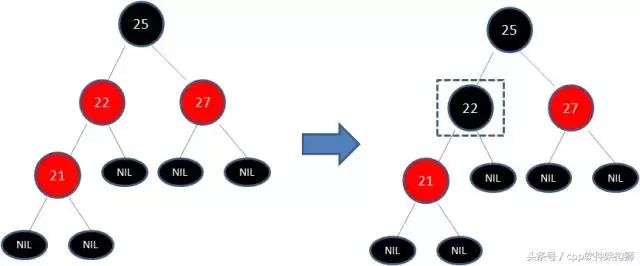
但这样还是不符合规则5,所以需要把25黑变红,看下图:
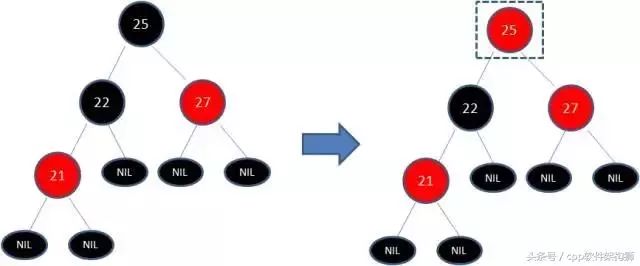
你以为现在结束了?天真,因为25和27又是两个连续的红色节点(规则4),所以需要将27红变黑。
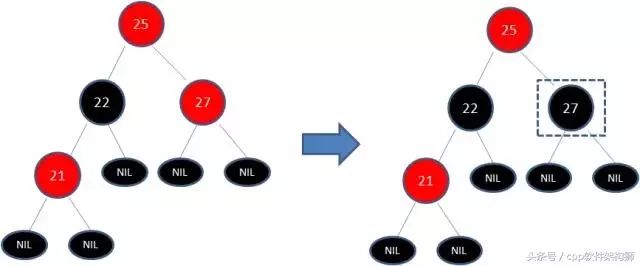
终于结束了,都满足规则了,舒服多了。
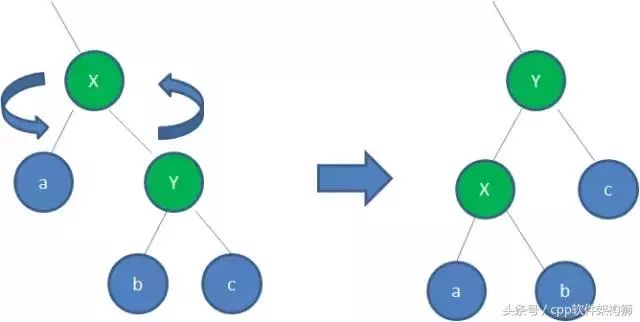
【左旋转】
也就是逆时针旋转两个节点,使父节点被自己的右孩子取代,而自己成为自己的左孩子,听起来吓死人,直接看图吧:
【右旋转】
顺时针旋转两个节点,使得自己的父节点被左孩子取代,而自己成为自己的右孩子,看不懂直接看图吧:
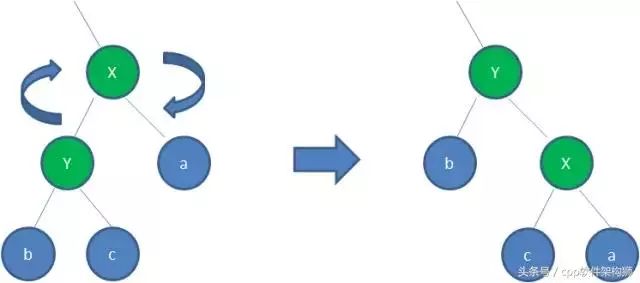
看起来这么复杂,到底怎么用呢?确实很复杂,我们讲下典型的例子,大家参考下:
以刚才插入21节点的例子:

首先我们需要做的是变色,把节点25以及下方的节点变色:
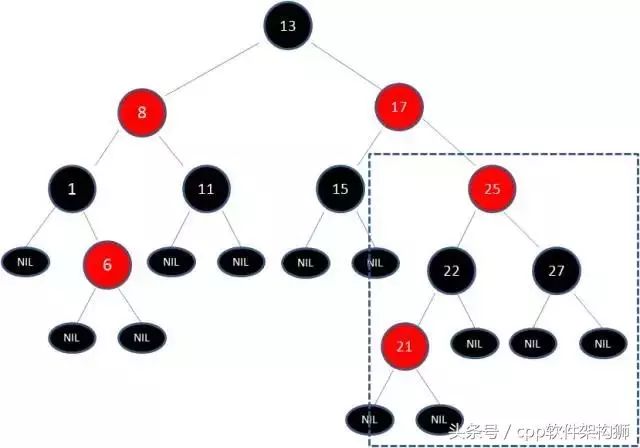
由于17和25是连续的两个红色节点,那么吧节点17变黑吗?这样是不行的,你想这样一来不就打破了规则4了吗,而且根据规则2,也不可能吧13变成红色。变色已经无法解决问题了,所以只能进行旋转了。13当成X,17当成Y,左旋转试试看:

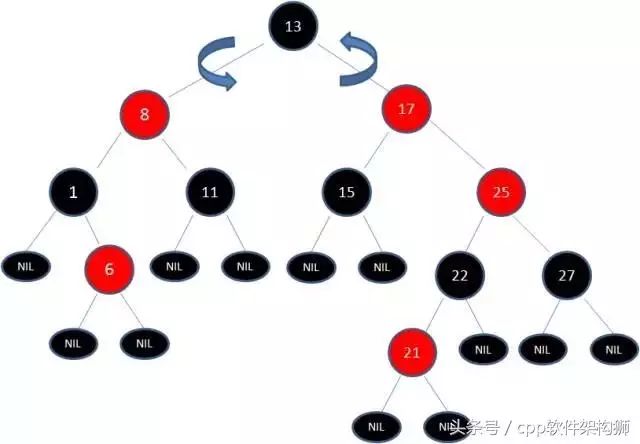
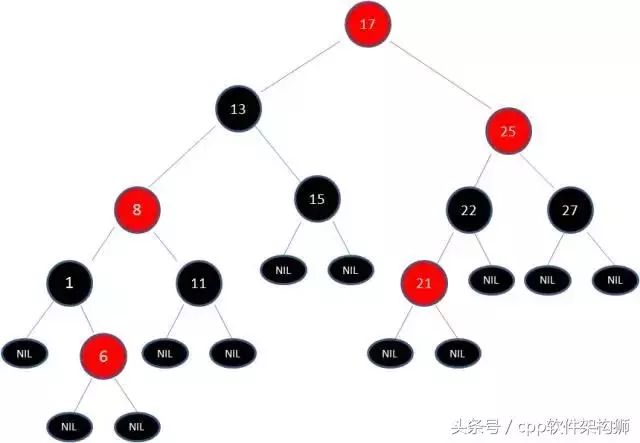
由于根节点必须是黑色,所以需要变色,结果如下图:
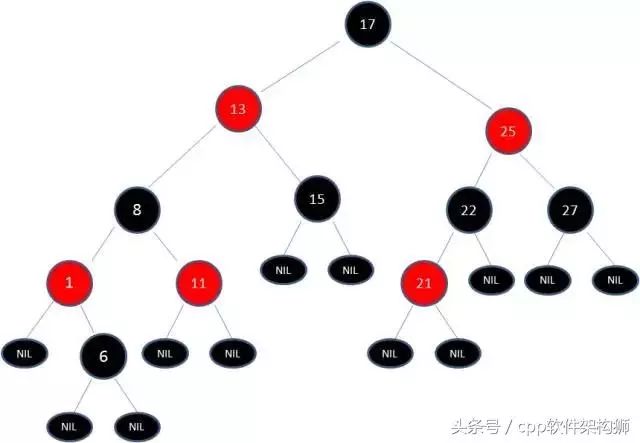
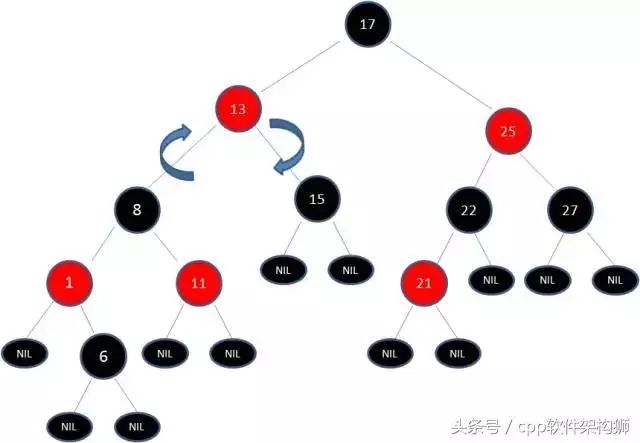
继续,其中有两条路径(17-)8->6->NULL)的黑色节点个数不是3,是4不符合规则。
这个时候需要把13当做X,8当做Y,进行右旋转:

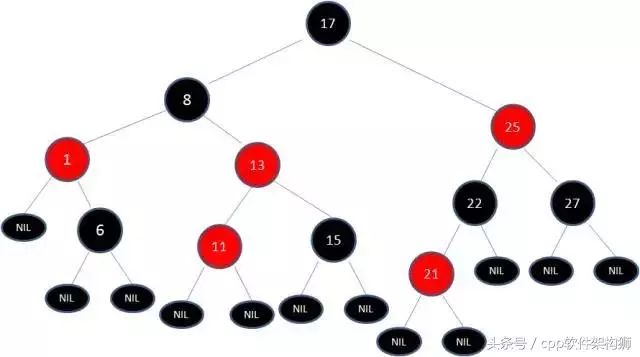
最后根据规则变色:
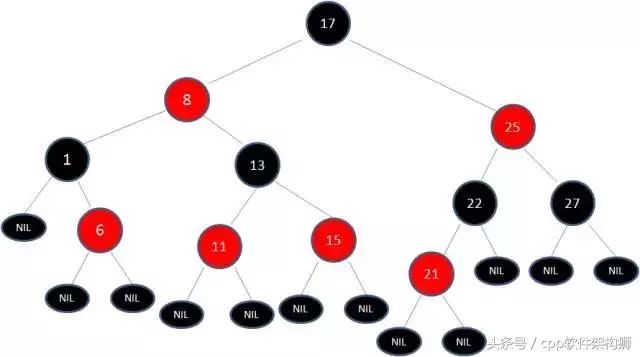
这样一来,我们终于结束了,经过调整之后符合规则。
那我们费这么大力气,这么复杂,这东西用在哪里,有哪些应用呢?
其实STL中的map就是用的红黑树。
转自:www.360doc.com
总结:
红黑色的大体思想就是上面描述的那样,里面还有很多情况要考虑,本文只是简单的讲述思想,大家有兴趣可以去百度上看各种情况的考虑。谢谢大家的支持!

扫码或长按关注
回复「 加群 」进入技术群聊







)








$)


