在此次新冠肺炎疫情防控过程中,对疫情发展趋势的科学预测显得尤为重要。而这背后,离不开对传染病传播规律的建模。今天,小编就带各位数学学子们来了解一下传染病的四大经典数学模型:SI/SIS/SIR/SEIR。其中用到了许多微分方程的知识,大家不妨在阅读过程中重温一下。


首先来介绍几类与传染病相关的人群表示:
易感者(Susceptible):有潜在感染风险的人群,数量记为S(t)
潜伏者(Exposed):已感染但仍处于潜伏期未发生症状的人群,数量记为E(t)
感染者(Infectious):感染并表现症状的人群,数量记为I(t)
康复者(Recovered):痊愈获得抗性的人群,数量记为R(t)


SI模型
(Susceptible-Infectious Model)
SI模型考虑了最简单的情况,即把人群分为易感者S和感染者I两类,且绝望地不考虑康复。假设总人数为N,单位时间I个感染者接触r个人,传染率为β,易感人比例为S/N,则单位时间新增病例为rβIS/N,可得到微分方程:
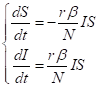
其初始条件为:
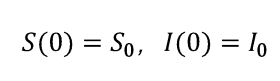
总人数守恒条件为:
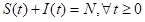
将S=N-I代入第二个微分方程即得:
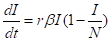
这就是我们学过的Logistic方程,解得:
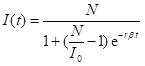
其指数增长率rβ,正比于感染者的接触人数和传染率。当感染者I达到N/2时病人增加速度最快。观察可得,
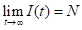
也就是此模型下经过足够时间人类将全军覆没。
我们用MATLAB来模拟SI模型下的增长过程。假设地区共有5000个人,最初只有1人感染,感染者每天出门遇到10个人,传染率是1%, 我们来看一看结果。
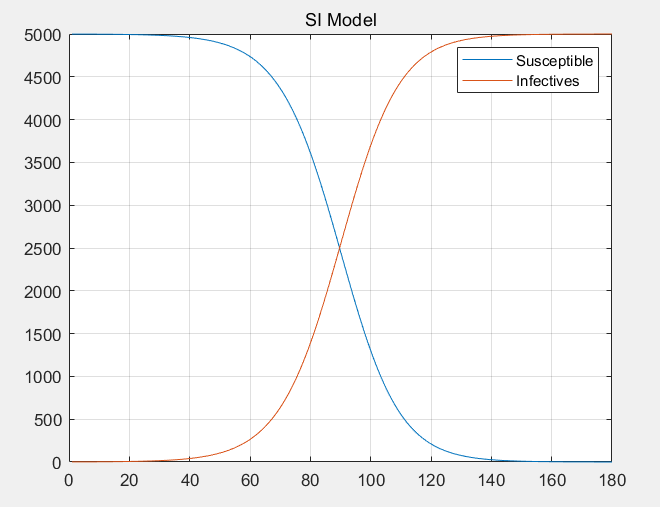
半年时间内一个人几乎传染给了所有人,SI模型告诉我们在对无望康复的传染病(如HIV)的控制中,隔离传染过程非常重要,否则最终整个生态将崩溃。

SIS模型
(Susceptible-Infectious-Susceptible Model)
接下来我们考虑稍微复杂而有希望的情况,即感染者可以康复,但令人沮丧的是康复者仍然可能再次被感染。例如普通流感常常应用这类模型。这种情况下需要向模型中添加感染者I的康复率γ,也就是单位时间内感染者会减少γI,而易感者会增加γI。
修正微分方程为:
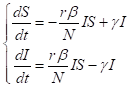
同样地,初始条件为:
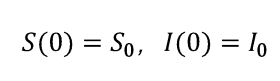
以及总人数守恒条件:
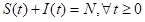
将S=N-I代入第二个微分方程即得:
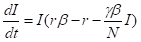
同样的方法可解得Logistic函数:
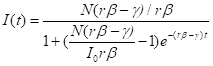
注意这次感染者I的极限并不是全部人口N,而是:
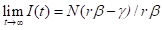
我们一样用MATLAB来验证一下,参数取值都与SI模型一样,不同的是添加了康复率γ,我们假设为3%。
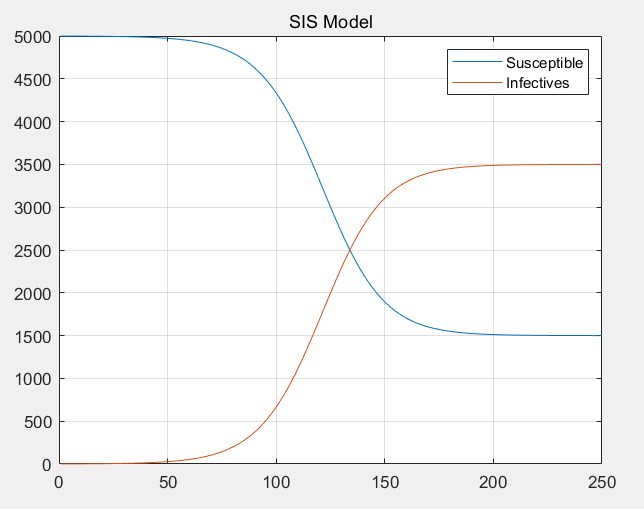
可见假设条件下一年内病人和健康人基本达到动态平衡,而最终稳定的健康人比例决于rβ和γ,即传染性和康复性。本例中其他条件不变的情况下如果康复率提高到10%,在极短的时间内病人数将几乎稳定在0,这出人意料的全员康复结果提示了提高医疗科研水平来增加康复率的重要性。

SIR模型
(Susceptible-Infectious-Recovered Model)
继续完善我们的数学模型。许多急性传染病康复后是存在抗体的,如有短期抗体的感冒,长期抗体的水痘、腮腺炎等。这些时候我们需要引入第三类人群:康复者R,假设此类人群体内拥有别人梦寐以求的抗体,得病后永不复发长生不死。单位时间康复者γI不再加入到S类,而是归为R类。
此时有三个微分方程:
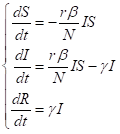
初始条件:
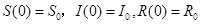
总人数守恒条件:
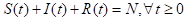
至此就不会求解析解啦,我们用数值解来模拟。还是假设地区共有5000个人,最初只有1人感染,感染者每天出门遇到10个人,传染率设为3%,康复率是5%。
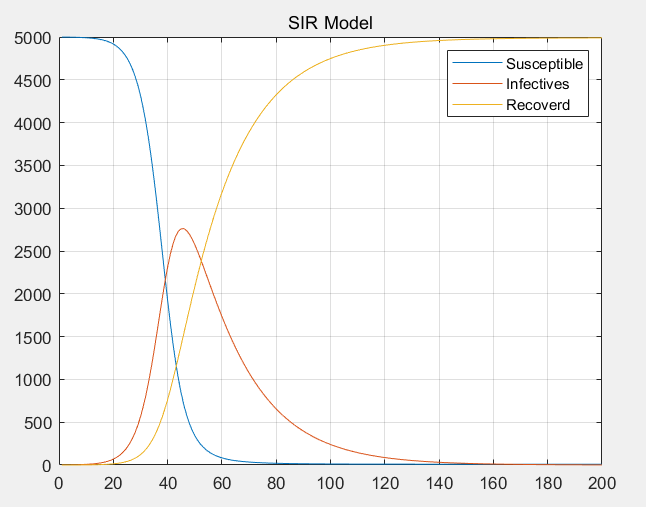
可以看到假设条件下传染病爆发40~50天疫情达到高峰,此后半年内逐渐平息,最后全员康复。这一模型和现实中我们常经历的急性传染病的传播阶段比较符合,这其中抗体起到一个非常关键的作用,也提示了痊愈者血清以及研制疫苗在遏制疫情上的重要性。

SEIR模型
(Susceptible-Exposed-Infectious-Recovered Model)
为了研究带潜伏期的恶性传染病,继续复杂化我们的模型。此时引入潜伏者E,潜伏者感染疾病但是不会显现症状,且不考虑潜伏期的传染性。这类模型就是当前2019-nCoV传播的基本模型。当然,实际情况要比理想模型复杂得多,还需考虑其他的扰动项来修正方程,我们只考察最原始最简单的SEIR模型。假设单位时间被感染者I以传染率β把易感者S变为潜伏者E,即E单位时间增加rβIS/N,而潜伏者以概率α发作成感染者,即E单位时间减少αE,I单位时间增加αE,康复者仍按之前假设。微分方程为:
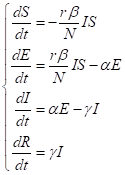
初始条件:
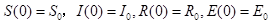
人数守恒:
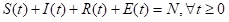
同样地,求不出解析解的情况下我们用数值模拟。为了更好地模拟新肺疫情,传染率取值较之前的例子有所提高。假设地区共有5000个人,最初只有1人感染,感染者每天出门遇到10个人,以10%的传染率把健康人变为潜伏者,潜伏者以50%的概率发作症状变为感染者,康复率是10%。
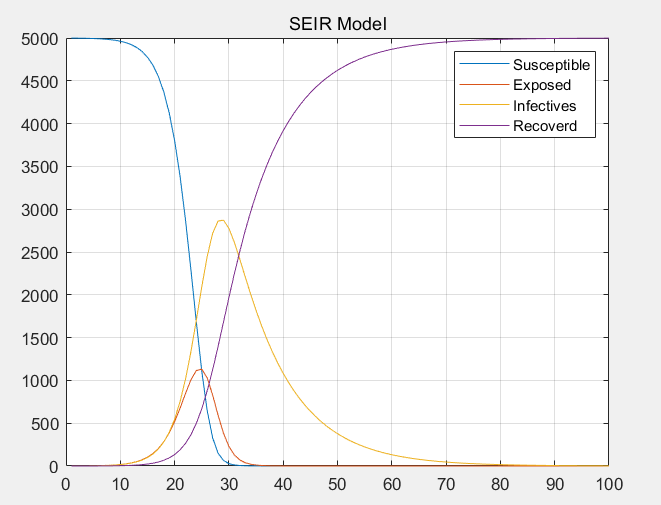
可见上述条件下在20~30天中潜伏期人群达到顶峰,而30天左右感染者达到顶峰,疫情迎来大爆炸,随着康复人群的上升,疫情在三个月左右基本结束。这大体上符合目前2019-nCoV的走势。同时可以看出疫情防控中,对感染者的隔离、对潜伏者的尽早识别和控制都是重中之重。
数学无处不在,通过以上模型的介绍,相信大家对传染病有了更加深入的认识。传染病防控离不开多个学科的合作,希望通过数学人的共同努力,让传染病防控水平得到进一步提升!
文编:网易羊
美编:陈茜
责编:王天晓













)

 方法)




