文章目录
- 转换器与估计器
- 分类算法-K近邻算法
- 一个例子弄懂k-近邻
- 计算距离公式
- sklearn.neighbors
- Method
- k近邻实例
- k-近邻算法案例分析
- 对Iris数据集进行分割
- 对特征数据进行标准化
- 朴素贝叶斯
- 概率论基础
- 联合概率与条件概率
- 联合概率
- 条件概率
- 如果每个事件相互独立
- 拉普拉斯平滑
- sklearn朴素贝叶斯实现API
- 朴素贝叶斯优缺点
- 词袋法特征值计算
- 案例
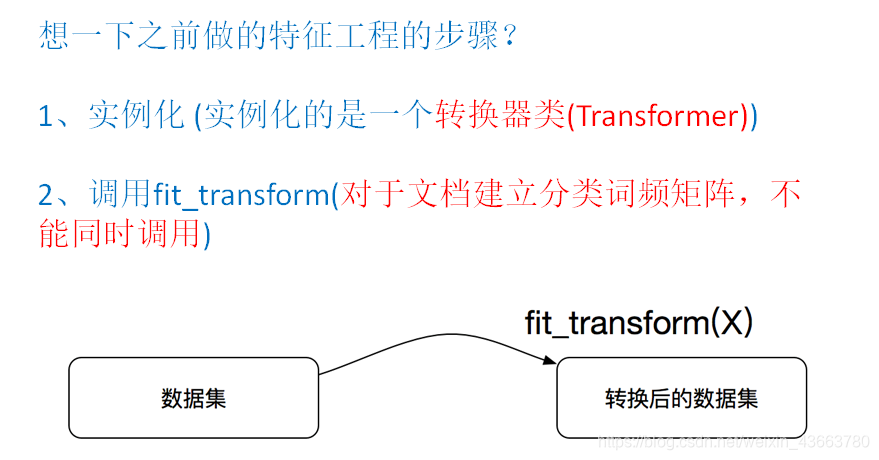
转换器与估计器



分类算法-K近邻算法
一个例子弄懂k-近邻
电影可以按照题材分类,每个题材又是如何定义的呢?那么假如两种类型的电影,动作片和爱情片。动作片有哪些公共的特征?那么爱情片又存在哪些明显的差别呢?我们发现动作片中打斗镜头的次数较多,而爱情片中接吻镜头相对更多。当然动作片中也有一些接吻镜头,爱情片中也会有一些打斗镜头。所以不能单纯通过是否存在打斗镜头或者接吻镜头来判断影片的类别。那么现在我们有6部影片已经明确了类别,也有打斗镜头和接吻镜头的次数,还有一部电影类型未知

那么我们使用K-近邻算法来分类爱情片和动作片:存在一个样本数据集合,也叫训练样本集,样本个数M个,知道每一个数据特征与类别对应关系,然后存在未知类型数据集合1个,那么我们要选择一个测试样本数据中与训练样本中M个的距离,排序过后选出最近的K个,这个取值一般不大于20个。选择K个最相近数据中次数最多的分类。那么我们根据这个原则去判断未知电影的分类

我们假设K为3,那么排名前三个电影的类型都是爱情片,所以我们判定这个未知电影也是一个爱情片。那么计算距离是怎样计算的呢?
欧氏距离 那么对于两个向量点
之间的距离,可以通过该公式表示


计算距离公式
欧氏距离
k近邻算法需要做标准化处理

sklearn.neighbors
sklearn.neighbors提供监督的基于邻居的学习方法的功能,sklearn.neighbors.KNeighborsClassifier是一个最近邻居分类器。那么KNeighborsClassifier是一个类,我们看一下实例化时候的参数
class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=1, **kwargs)**""":param n_neighbors:int,可选(默认= 5),k_neighbors查询默认使用的邻居数:param algorithm:{'auto','ball_tree','kd_tree','brute'},可选用于计算最近邻居的算法:'ball_tree'将会使用 BallTree,'kd_tree'将使用 KDTree,“野兽”将使用强力搜索。'auto'将尝试根据传递给fit方法的值来决定最合适的算法。:param n_jobs:int,可选(默认= 1),用于邻居搜索的并行作业数。如果-1,则将作业数设置为CPU内核数。不影响fit方法。"""
import numpy as np
from sklearn.neighbors import KNeighborsClassifierneigh = KNeighborsClassifier(n_neighbors=3)
Method
fit(X, y)
使用X作为训练数据拟合模型,y作为X的类别值。X,y为数组或者矩阵
X = np.array([[1,1],[1,1.1],[0,0],[0,0.1]])
y = np.array([1,1,0,0])
neigh.fit(X,y)
kneighbors(X=None, n_neighbors=None, return_distance=True)
找到指定点集X的n_neighbors个邻居,return_distance为False的话,不返回距离
neigh.kneighbors(np.array([[1.1,1.1]]),return_distance= False)neigh.kneighbors(np.array([[1.1,1.1]]),return_distance= False,n_neighbors=2)
predict(X)
预测提供的数据的类标签
neigh.predict(np.array([[0.1,0.1],[1.1,1.1]]))
predict_proba(X)
返回测试数据X属于某一类别的概率估计
neigh.predict_proba(np.array([[1.1,1.1]]))
k近邻实例



def knncls():"""K-近邻预测用户签到位置:return:None"""# 读取数据data = pd.read_csv("./data/FBlocation/train.csv")# print(data.head(10))# 处理数据# 1、缩小数据,查询数据晒讯data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")# 处理时间的数据time_value = pd.to_datetime(data['time'], unit='s')print(time_value)# 把日期格式转换成 字典格式time_value = pd.DatetimeIndex(time_value)# 构造一些特征data['day'] = time_value.daydata['hour'] = time_value.hourdata['weekday'] = time_value.weekday# 把时间戳特征删除data = data.drop(['time'], axis=1)print(data)# 把签到数量少于n个目标位置删除place_count = data.groupby('place_id').count()tf = place_count[place_count.row_id > 3].reset_index()data = data[data['place_id'].isin(tf.place_id)]# 取出数据当中的特征值和目标值y = data['place_id']x = data.drop(['place_id'], axis=1)# 进行数据的分割训练集合测试集x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)# 特征工程(标准化)std = StandardScaler()# 对测试集和训练集的特征值进行标准化x_train = std.fit_transform(x_train)x_test = std.transform(x_test)# 进行算法流程 # 超参数knn = KNeighborsClassifier()# # fit, predict,score# knn.fit(x_train, y_train)## # 得出预测结果# y_predict = knn.predict(x_test)## print("预测的目标签到位置为:", y_predict)## # 得出准确率# print("预测的准确率:", knn.score(x_test, y_test))# 构造一些参数的值进行搜索param = {"n_neighbors": [3, 5, 10]}# 进行网格搜索gc = GridSearchCV(knn, param_grid=param, cv=2)gc.fit(x_train, y_train)# 预测准确率print("在测试集上准确率:", gc.score(x_test, y_test))print("在交叉验证当中最好的结果:", gc.best_score_)print("选择最好的模型是:", gc.best_estimator_)print("每个超参数每次交叉验证的结果:", gc.cv_results_)return None
C:\Users\HP\Anaconda3\python.exe D:/PycharmProjects/untitled2/算法/算法3.pyrow_id x y accuracy time place_id
0 0 0.7941 9.0809 54 470702 8523065625
1 1 5.9567 4.7968 13 186555 1757726713
2 2 8.3078 7.0407 74 322648 1137537235
3 3 7.3665 2.5165 65 704587 6567393236
4 4 4.0961 1.1307 31 472130 7440663949
5 5 3.8099 1.9586 75 178065 6289802927
6 6 6.3336 4.3720 13 666829 9931249544
7 7 5.7409 6.7697 85 369002 5662813655
8 8 4.3114 6.9410 3 166384 8471780938
9 9 6.3414 0.0758 65 400060 1253803156
600 1970-01-01 18:09:40
957 1970-01-10 02:11:10
4345 1970-01-05 15:08:02
4735 1970-01-06 23:03:03
5580 1970-01-09 11:26:50
6090 1970-01-02 16:25:07
6234 1970-01-04 15:52:57
6350 1970-01-01 10:13:36
7468 1970-01-09 15:26:06
8478 1970-01-08 23:52:02
9357 1970-01-04 16:53:19
12125 1970-01-07 03:55:07
14937 1970-01-06 03:46:38
20660 1970-01-08 03:08:15
20930 1970-01-02 21:31:48
21731 1970-01-07 08:52:19
26584 1970-01-04 15:48:09
27937 1970-01-08 03:51:54
30798 1970-01-01 20:58:30
33184 1970-01-06 15:31:39
33877 1970-01-02 14:58:01
34340 1970-01-04 14:03:40
37405 1970-01-04 15:35:01
38968 1970-01-08 08:56:00
41861 1970-01-01 03:13:36
42135 1970-01-02 02:36:41
42729 1970-01-01 16:03:37
44283 1970-01-08 06:48:09
44549 1970-01-07 01:10:01
44694 1970-01-08 14:30:07...
29070221 1970-01-07 02:55:07
29070322 1970-01-01 18:13:24
29070934 1970-01-03 03:44:08
29071712 1970-01-08 04:19:17
29072165 1970-01-04 12:42:07
29073572 1970-01-07 20:29:38
29074121 1970-01-08 02:30:21
29077579 1970-01-08 18:08:30
29077716 1970-01-09 11:51:11
29079070 1970-01-07 00:33:24
29079416 1970-01-05 10:48:15
29079931 1970-01-02 05:35:45
29083241 1970-01-02 00:35:10
29083789 1970-01-05 09:39:49
29084739 1970-01-06 12:04:17
29085497 1970-01-03 11:31:33
29086167 1970-01-08 01:04:37
29087094 1970-01-04 22:25:01
29089004 1970-01-01 23:26:24
29090443 1970-01-03 09:00:22
29093677 1970-01-07 10:03:36
29094547 1970-01-09 11:44:34
29096155 1970-01-04 08:07:44
29099420 1970-01-04 15:47:47
29099686 1970-01-08 01:24:11
29100203 1970-01-01 10:33:56
29108443 1970-01-07 23:22:04
29109993 1970-01-08 15:03:14
29111539 1970-01-04 00:53:41
29112154 1970-01-08 23:01:07
Name: time, Length: 17710, dtype: datetime64[ns]
D:/PycharmProjects/untitled2/算法/算法3.py:36: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value insteadSee the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copydata['day']=time_value.day
D:/PycharmProjects/untitled2/算法/算法3.py:37: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value insteadSee the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copydata['hour']=time_value.hour
D:/PycharmProjects/untitled2/算法/算法3.py:38: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value insteadSee the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copydata['weekday']=time_value.weekdayrow_id x y accuracy place_id day hour weekday
600 600 1.2214 2.7023 17 6683426742 1 18 3
957 957 1.1832 2.6891 58 6683426742 10 2 5
4345 4345 1.1935 2.6550 11 6889790653 5 15 0
4735 4735 1.1452 2.6074 49 6822359752 6 23 1
5580 5580 1.0089 2.7287 19 1527921905 9 11 4
6090 6090 1.1140 2.6262 11 4000153867 2 16 4
6234 6234 1.1449 2.5003 34 3741484405 4 15 6
6350 6350 1.0844 2.7436 65 5963693798 1 10 3
7468 7468 1.0058 2.5096 66 9076695703 9 15 4
8478 8478 1.2015 2.5187 72 3992589015 8 23 3
9357 9357 1.1916 2.7323 170 5163401947 4 16 6
12125 12125 1.1388 2.5029 69 7536975002 7 3 2
14937 14937 1.1426 2.7441 11 6780386626 6 3 1
20660 20660 1.2387 2.5959 65 3683087833 8 3 3
20930 20930 1.0519 2.5208 67 6399991653 2 21 4
21731 21731 1.2171 2.7263 99 8048985799 7 8 2
26584 26584 1.1235 2.6282 63 5606572086 4 15 6
27937 27937 1.1287 2.6332 588 5606572086 8 3 3
30798 30798 1.0422 2.6474 49 1435128522 1 20 3
33184 33184 1.0128 2.5865 75 1913341282 6 15 1
33877 33877 1.1437 2.6972 972 6683426742 2 14 4
34340 34340 1.1513 2.5824 176 2355236719 4 14 6
37405 37405 1.2122 2.7106 10 2946102544 4 15 6
38968 38968 1.1496 2.6298 166 9598377925 8 8 3
41861 41861 1.0886 2.6840 10 3312463746 1 3 3
42135 42135 1.0498 2.6840 5 3312463746 2 2 4
42729 42729 1.0694 2.5829 10 1812226671 1 16 3
44283 44283 1.2384 2.7398 60 8048985799 8 6 3
44549 44549 1.2077 2.5370 76 3992589015 7 1 2
44694 44694 1.0380 2.5315 152 5035268417 8 14 3
... ... ... ... ... ... ... ... ...
29070221 29070221 1.1678 2.5605 66 2355236719 7 2 2
29070322 29070322 1.0493 2.7010 74 3312463746 1 18 3
29070934 29070934 1.1899 2.5176 28 2199223958 3 3 5
29071712 29071712 1.2260 2.7367 4 2946102544 8 4 3
29072165 29072165 1.0175 2.6220 42 5283227804 4 12 6
29073572 29073572 1.2467 2.7316 64 8048985799 7 20 2
29074121 29074121 1.2071 2.6646 161 5270522918 8 2 3
29077579 29077579 1.2479 2.6474 42 2006503124 8 18 3
29077716 29077716 1.1898 2.7013 5 6683426742 9 11 4
29079070 29079070 1.1882 2.5476 28 1731306153 7 0 2
29079416 29079416 1.2335 2.5903 72 6766324666 5 10 0
29079931 29079931 1.0213 2.6554 167 5270522918 2 5 4
29083241 29083241 1.0600 2.6722 71 9632980559 2 0 4
29083789 29083789 1.0674 2.6184 88 1097200869 5 9 0
29084739 29084739 1.2319 2.6767 63 2327054745 6 12 1
29085497 29085497 1.0550 2.5997 175 1097200869 3 11 5
29086167 29086167 1.0515 2.6758 57 6237569496 8 1 3
29087094 29087094 1.0088 2.5978 71 1097200869 4 22 6
29089004 29089004 1.1860 2.6926 153 2215268322 1 23 3
29090443 29090443 1.0568 2.6959 58 2460093296 3 9 5
29093677 29093677 1.0016 2.5252 16 9013153173 7 10 2
29094547 29094547 1.1101 2.6530 24 5270522918 9 11 4
29096155 29096155 1.0122 2.6450 65 8178619377 4 8 6
29099420 29099420 1.1675 2.5556 9 2355236719 4 15 6
29099686 29099686 1.0405 2.6723 13 3312463746 8 1 3
29100203 29100203 1.0129 2.6775 12 3312463746 1 10 3
29108443 29108443 1.1474 2.6840 36 3533177779 7 23 2
29109993 29109993 1.0240 2.7238 62 6424972551 8 15 3
29111539 29111539 1.2032 2.6796 87 3533177779 4 0 6
29112154 29112154 1.1070 2.5419 178 4932578245 8 23 3[17710 rows x 8 columns]
C:\Users\HP\Anaconda3\lib\site-packages\sklearn\preprocessing\data.py:645: DataConversionWarning: Data with input dtype int64, float64 were all converted to float64 by StandardScaler.return self.partial_fit(X, y)
C:\Users\HP\Anaconda3\lib\site-packages\sklearn\base.py:464: DataConversionWarning: Data with input dtype int64, float64 were all converted to float64 by StandardScaler.return self.fit(X, **fit_params).transform(X)
D:/PycharmProjects/untitled2/算法/算法3.py:62: DataConversionWarning: Data with input dtype int64, float64 were all converted to float64 by StandardScaler.x_test=std.transform(x_test)
C:\Users\HP\Anaconda3\lib\site-packages\sklearn\model_selection\_split.py:652: Warning: The least populated class in y has only 1 members, which is too few. The minimum number of members in any class cannot be less than n_splits=2.% (min_groups, self.n_splits)), Warning)
在测试集上准确率 0.42174940898345153
在交叉验证中最好结果 0.3899747793190416
选择最好的模型 KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',metric_params=None, n_jobs=None, n_neighbors=10, p=2,weights='uniform')
每个超参数每次交叉验证的结果 {'mean_fit_time': array([0.01645494, 0.01138353, 0.01047194]), 'std_fit_time': array([0.00448656, 0.00058341, 0.00249255]), 'mean_score_time': array([0.75878692, 0.61585569, 0.6273967 ]), 'std_score_time': array([0.01371908, 0.09724212, 0.01204288]), 'param_n_neighbors': masked_array(data=[3, 5, 10],mask=[False, False, False],fill_value='?',dtype=object), 'params': [{'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 10}], 'split0_test_score': array([0.33999688, 0.36842105, 0.38841168]), 'split1_test_score': array([0.34622116, 0.37549722, 0.39156722]), 'mean_test_score': array([0.34308008, 0.37192623, 0.38997478]), 'std_test_score': array([0.00311201, 0.00353793, 0.0015777 ]), 'rank_test_score': array([3, 2, 1]), 'split0_train_score': array([0.60875099, 0.56022275, 0.49880668]), 'split1_train_score': array([0.59253475, 0.53959082, 0.48633453]), 'mean_train_score': array([0.60064287, 0.54990678, 0.49257061]), 'std_train_score': array([0.00810812, 0.01031597, 0.00623608])}Process finished with exit code 0k-近邻算法案例分析
本案例使用最著名的”鸢尾“数据集,该数据集曾经被Fisher用在经典论文中,目前作为教科书般的数据样本预存在Scikit-learn的工具包中
from sklearn.datasets import load_iris
# 使用加载器读取数据并且存入变量iris
iris = load_iris()# 查验数据规模
iris.data.shape# 查看数据说明(这是一个好习惯)
print iris.DESCR
通过上述代码对数据的查验以及数据本身的描述,我们了解到Iris数据集共有150朵鸢尾数据样本,并且均匀分布在3个不同的亚种;每个数据样本有总共4个不同的关于花瓣、花萼的形状特征所描述。由于没有制定的测试集合,因此按照惯例,我们需要对数据进行随即分割,25%的样本用于测试,其余75%的样本用于模型的训练。
由于不清楚数据集的排列是否随机,可能会有按照类别去进行依次排列,这样训练样本的不均衡的,所以我们需要分割数据,已经默认有随机采样的功能
对Iris数据集进行分割
from sklearn.cross_validation import train_test_split
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,test_size=0.25,random_state=42)
对特征数据进行标准化
from sklearn.preprocessing import StandardScalerss = StandardScaler()
X_train = ss.fit_transform(X_train)
X_test = ss.fit_transform(X_test)
K近邻算法是非常直观的机器学习模型,我们可以发现K近邻算法没有参数训练过程,也就是说,我们没有通过任何学习算法分析训练数据,而只是根据测试样本训练数据的分布直接作出分类决策。因此,K近邻属于无参数模型中非常简单一种。
from sklearn.datasets import load_iris
from sklearn.cross_validation import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report
from sklearn.model_selection import GridSearchCVdef knniris():"""鸢尾花分类:return: None"""# 数据集获取和分割lr = load_iris()x_train, x_test, y_train, y_test = train_test_split(lr.data, lr.target, test_size=0.25)# 进行标准化std = StandardScaler()x_train = std.fit_transform(x_train)x_test = std.transform(x_test)# estimator流程knn = KNeighborsClassifier()# # 得出模型# knn.fit(x_train,y_train)## # 进行预测或者得出精度# y_predict = knn.predict(x_test)## # score = knn.score(x_test,y_test)# 通过网格搜索,n_neighbors为参数列表param = {"n_neighbors": [3, 5, 7]}gs = GridSearchCV(knn, param_grid=param, cv=10)# 建立模型gs.fit(x_train,y_train)# print(gs)# 预测数据print(gs.score(x_test,y_test))# 分类模型的精确率和召回率# print("每个类别的精确率与召回率:",classification_report(y_test, y_predict,target_names=lr.target_names))return Noneif __name__ == "__main__":knniris()
朴素贝叶斯
朴素贝叶斯(Naive Bayes)是一个非常简单,但是实用性很强的分类模型。朴素贝叶斯分类器的构造基础是贝叶斯理论。
概率论基础
概率定义为一件事情发生的可能性。事情发生的概率可以 通过观测数据中的事件发生次数来计算,事件发生的概率等于改事件发生次数除以所有事件发生的总次数。举一些例子:
扔出一个硬币,结果头像朝上
某天是晴天
某个单词在未知文档中出现

联合概率与条件概率
联合概率
是指两件事情同时发生的概率。那么我们假设样本空间有一些天气数据: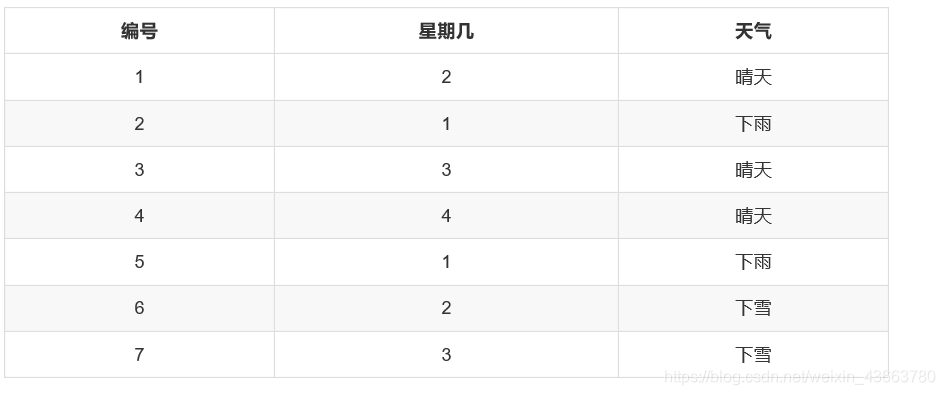

条件概率

如果每个事件相互独立

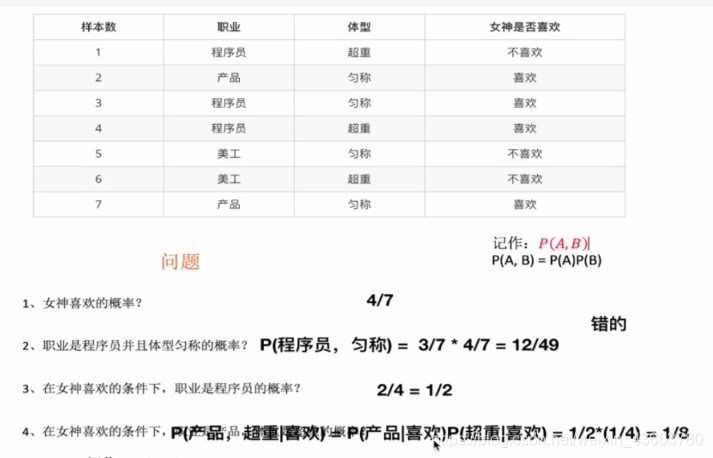




拉普拉斯平滑



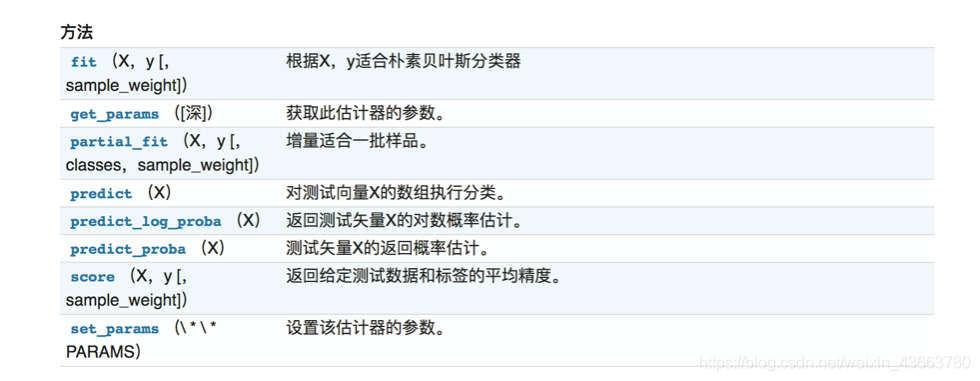
sklearn朴素贝叶斯实现API


class sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)""":param alpha:float,optional(default = 1.0)加法(拉普拉斯/ Lidstone)平滑参数(0为无平滑)"""
朴素贝叶斯优缺点

词袋法特征值计算


案例
互联网新闻分类
def naviebayes():"""朴素贝叶斯进行文本分类:return: None"""news=fetch_20newsgroups(subset='all')#进行数据分割x_train,x_test,y_train,y_test=train_test_split(news.data,news.target,test_size=0.25)#对数据集进行特征抽取tf=TfidfVectorizer()# 以训练集当中的词的列表进行每篇文章重要性统计['a','b','c','d']x_train=tf.fit_transform(x_train)# print(tf.get_feature_names())x_test=tf.transform(x_test)#进行朴素贝叶斯预测mlt=MultinomialNB(alpha=1.0)# print(x_train.toarray())mlt.fit(x_train,y_train)y_predict=mlt.predict(x_test)print("预测文章类别",y_predict)#得出准确率# print("准确率为",mlt.score(x_test,y_test))# print("每个类别准确率和召回率",classification_report(y_test,y_predict,target_names=news.target_names))return None






![[芦半山]Android native分析工具ASAN和HWASAN原理解析](http://pic.xiahunao.cn/[芦半山]Android native分析工具ASAN和HWASAN原理解析)











开机引导失败出现grub rescue的修复办法...)
端口冲突解决办法)