编程之美-第3章结构之法

3.1. 字符串移位包含问题

clip_image002

方法1:

分别对字符串进行循环移1位,2位,3位…,来判断给定的字符串是否是其中一个字串.

复杂度是O(n^3)

clip_image004

方法2:

clip_image006

这也是一种利用空间换时间的方法.

代码如下, 为了简便实现,采用了C库中的字符串操作函数:

#if 0
/** 3.1*/
bool isRotate(char *s1,char* s2){int len1=strlen(s1),len2=strlen(s2);char *ss=new char[2*len1+1];strncpy(ss,s1,len1);strncat(ss,s2,len1);char *p=strstr(ss,s2);bool flag;if(p==0)flag=false;elseflag=true;delete[] ss;return true;
}
int main(){char *s1="ABCD";char *s2="CDAB";if(isRotate(s1,s2))printf("OK");elseprintf("NO");}#endif

也可以采用KMP算法进行加快查找: http://blog.csdn.net/linyunzju/article/details/7745553

3.2 电话号码对应英语单词问题

clip_image008

这个问题可以直观的用下面的图来表示

clip_image010

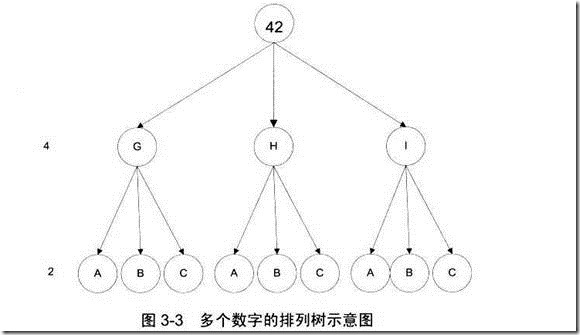
这样对于一个号码所对应的单词, 可以使用对树进行搜索的方式进行.

这种情况下采用的是DFS的方式.

下面的代码中采用了两种方式, 递归和非递归的方式. 其实这就是一个组合问题, 需要遍历所有情况. 对于非递归的情况, 其实有些类似非递归的排列组合的方式.

#if 0
char *c[10]{"","","ABC","DEF","GHI","JKL","MNO","PQRS","TUV","WXYZ" 
};
int total[10]={0,0,3,3,3,3,3, 4,3,4};
void transform(char *number){int sz=strlen(number);int *answer=new int[sz]();while(1){for(int i=0;i<sz;i++)printf("%c",c[number[i]-'0'][answer[i]]);printf("\n");int k=sz-1;while(k>=0){if(answer[k]<total[number[k]-'0']-1){answer[k]++;break;}else{answer[k]=0;k--;}}if(k<0)break;}delete[] answer;
}
void dfs(char *number,int *answer,int k,int sz){if(k==sz){for(int i=0;i<sz;i++)printf("%c",c[number[i]-'0'][answer[i]]);printf("\n");}else{for(answer[k]=0;answer[k]<total[number[k]-'0'];answer[k]++)dfs(number,answer,k+1,sz);}}
void transform2(char *number){int sz=strlen(number);int *answer=new int[sz]();dfs(number,answer,0,sz);delete[] answer;
}
int main(){char *number="2345";transform(number);transform2(number);
}#endif

对于问题二,可以采用下面的解法:

clip_image012

3.3 计算字符串相似度问题(编辑距离问题)

clip_image014

这个问题就是编辑距离的问题.

可以有两种解决方式: 递归的方式和动态规划的方式.

方法1: 递归的方式

clip_image016

这样就得到了下面的递归程序:

#if 0
/** 3.3*/
int calc_edit_dist(char *s1,char *s2){if(*s1=='\0'||s1==0)return strlen(s2);if(*s2=='\0'||s2==0)return strlen(s1);if(*s1==*s2){return calc_edit_dist(s1+1,s2+1);}else{int ed1=calc_edit_dist(s1,s2+1);int ed2=calc_edit_dist(s1+1,s2);int ed3=calc_edit_dist(s1+1,s2+1);if(ed1<ed2)return (ed1<ed3?ed1:ed3)+1;elsereturn (ed2<ed3?ed2:ed3)+1;}
}
int main(){char *s1="ab";char *s2="bb";printf("%d\n",calc_edit_dist(s1,s2));}#endif

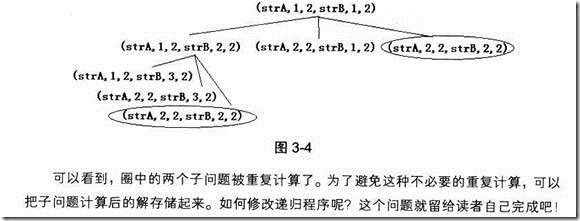
但是递归程序计算比较慢, 因为中间存在很多的重复计算.

clip_image018 \

方法2: 动态规划

这个问题其实可以归结为寻找两个序列的最长公共子序列问题.

参考: http://blog.csdn.net/linyunzju/article/details/7747718

3.5 最短摘要生成问题

给定一段产品的英文描述，包含M个英文字母，每个英文单词以空格分隔，无其他标点符号；再给定N个英文单词关键字，请说明思路并编程实现方法String extractSummary(String description,String[] key words)，目标是找出此产品描述中包含N个关键字（每个关键词至少出现一次）的长度最短的子串，作为产品简介输出。（不限编程语言）20分。

clip_image020

#if 0
bool allExisted(const map<string,int>& mp){map<string,int>::const_iterator ite;for(ite=mp.begin();ite!=mp.end();++ite)if(ite->second==0)return false;return true;
}
void reset(map<string,int>& mp){map<string,int>::iterator ite;for(ite=mp.begin();ite!=mp.end();++ite)ite->second=0;
}
int find_min_len_digest(const vector<string>& vec,const vector<string>& keywords){map<string,int> mp;int len=1000000;vector<string>::const_iterator ite,pbeg,pend;for(ite=keywords.begin();ite!=keywords.end();++ite)mp[*ite]=0;pbeg=vec.begin();while(pbeg!=vec.end()){while(pbeg!=vec.end()&&mp.find(*pbeg)==mp.end())++pbeg;if(pbeg==vec.end())break;mp[*pbeg]++;pend=pbeg+1;while(pend!=vec.end()&&!allExisted(mp)){if(mp.find(*pend)==mp.end()) {++pend;}else{mp[*pend]++;++pend;}}if(allExisted(mp)){if(pend!=vec.end()){if(len>pend-pbeg){len=pend-pbeg;}for(ite=pbeg;ite!=pend;++ite)cout<<*ite<<' ';cout<<'\n';}else{if(len>vec.size()-(pbeg-vec.begin()))len=vec.size()-(pbeg-vec.begin());for(ite=pbeg;ite!=vec.end();++ite)cout<<*ite<<' ';cout<<'\n';break;}reset(mp);}pbeg=pend;}return len;
}
int main(){
//    string str[]={"i","am","a","big","boy",".","i","is","i","boy"};
//      string key[]={"i","boy"};
string key[] = { "微软", "计算机", "亚洲"};string str[] = { "微软","亚洲","研究院","成立","于","1998","年","，","我们","的","使命","是","使","未来","的","计算机","能够","看","、","听","、","学","，","能","用","自然语言","与","人类","进行","交流","。","在","此","基础","上","，","微软","亚洲","研究院","还","将","促进","计算机","在","亚太","地区","的","普及","，","改善","亚太","用户","的","计算","体验","。","”"};vector<string> keywords(key,key+sizeof(key)/sizeof(string));vector<string> vec(str,str+sizeof(str)/sizeof(string));//  copy(vec.begin(),vec.end(),ostream_iterator<string>(cout," "));
//  cout<<endl;
find_min_len_digest(vec,keywords);}#endif

3.6 判断两个链表是否相交

clip_image022

clip_image024 clip_image026 clip_image028 clip_image030

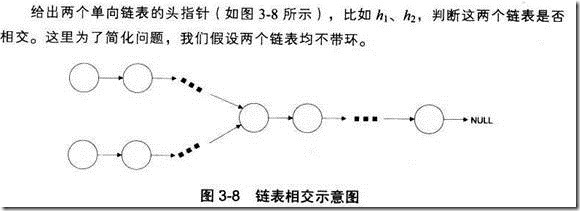
参考: http://blog.csdn.net/linyunzju/article/details/7753548

3.7 队列中取最大值操作问题

clip_image032

clip_image034

clip_image036

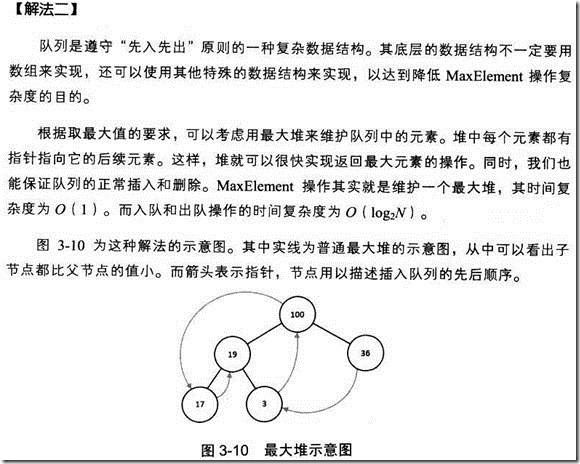
参考: http://blog.csdn.net/linyunzju/article/details/7765324

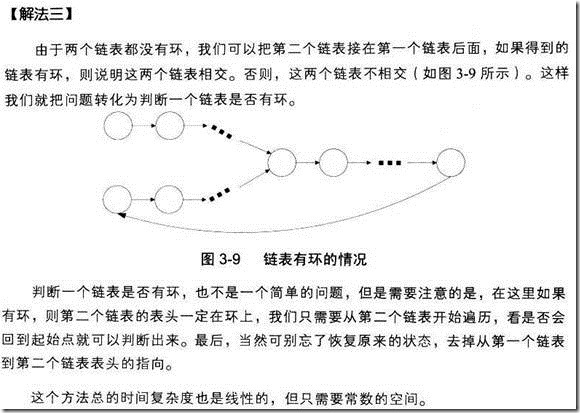
解法三:

利用两个STL中的stack适配器来实现带有最大值操作的栈类, 然后利用两个新实现的栈来实现带有最大值操作的队列.

#if 0
class Stack{public:void push(int x){sta.push(x);if(stb.empty()) {stb.push(x);}else{int t=stb.top();stb.push(t>x?t:x);}}void pop(){if(!sta.empty()){sta.pop();stb.pop();}}int top(){assert(sta.empty()==false);return sta.top();}int maxV(){assert(sta.empty()==false);return stb.top();}int size(){return sta.size();}bool empty(){return sta.empty();}private:stack<int> sta;stack<int> stb;
};
class Queue{public:void push(int x){sta.push(x);}void pop(){if(stb.empty()) {while(!sta.empty()) {int t=sta.top(); sta.pop();stb.push(t);}}stb.pop();}int front(){if(stb.empty()) {while(!sta.empty()){int t=sta.top(); sta.pop();stb.push(t);}}return stb.top();}int maxV(){if(stb.empty()){return sta.maxV();}if(sta.empty()){return stb.maxV();}return max(sta.maxV(),stb.maxV());}private:Stack sta;Stack stb;
};
int main(){Queue q;  int a[] = {2, 3, 4, 9, 4, 5, 10, 6};  for(int i = 0; i < sizeof(a)/sizeof(int); ++i) {  q.push(a[i]);  }  q.push(101);cout<<q.front()<<endl;cout<<"queue maxvalue = "<<q.maxV()<<endl;  q.push(590);cout<<"queue maxvalue = "<<q.maxV()<<endl;  int deq = q.front();  cout<<"deq = "<<deq<<endl;  cout<<"queue maxvalue = "<<q.maxV()<<endl;  q.pop();cout<<"queue maxvalue = "<<q.maxV()<<endl;  
}#endif

3.8 求二叉树中节点的最大距离

clip_image037

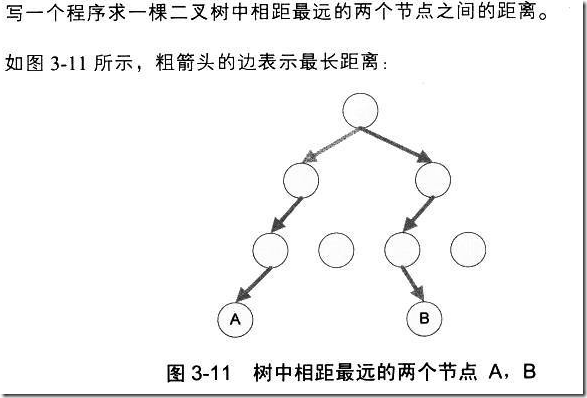
计算一个二叉树的最大距离有两个情况:

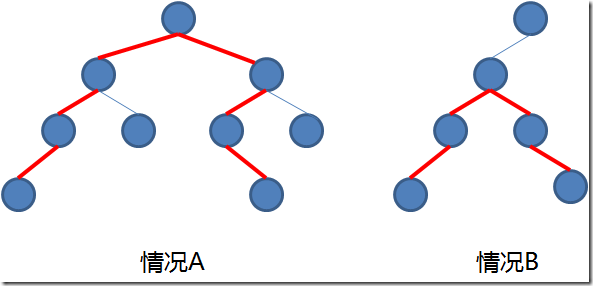
情况A: 路径经过左子树的最深节点，通过根节点，再到右子树的最深节点。

情况B: 路径不穿过根节点，而是左子树或右子树的最大距离路径，取其大者。

只需要计算这两个情况的路径距离，并取其大者，就是该二叉树的最大距离。

clip_image038

//思路：注意指针声明了一定要赋值，否则会报错。

// 方法一：递归法

//距离相差最远的两个结点，共有以下两种情况：

// (1)路径经过根结点，所以两个结点在根结点的不同分支上

// (2)路径不经过根结点，所以两个结点应该是次根结点中相聚最远的两个结点。(递归思想)

// 递归本质上还是采用了后续遍历的方法。由于是从叶子结点开始的所以每次处理都是第一种情况。

// 方法二：非递归法

//采用后序遍历二叉树的同时对二叉树的结点进行更新，每次更新都要更新最大距离。

struct Node{char data;Node* left;Node* right;int nMaxLeft;int nMaxRight;
};
int maxLen=0;
void findMaxLength(Node* root){if(root==0)return ;if(root->left==0)root->nMaxLeft=0;if(root->right==0)root->nMaxRight=0;if(root->left!=0)findMaxLength(root->left);if(root->right!=0)findMaxLength(root->right);if(root->left!=0) {root->nMaxLeft=(root->left->nMaxLeft>root->left->nMaxRight?root->left->nMaxLeft:root->left->nMaxRight)+1;}if(root->right!=0){root->nMaxRight=(root->right->nMaxLeft>root->right->nMaxRight?root->right->nMaxLeft:root->right->nMaxRight)+1;}if(root->nMaxLeft+root->nMaxRight>maxLen)maxLen=root->nMaxLeft+root->nMaxRight;
}
void findMaxLength2(Node* root){stack<Node*> st;Node *p=root,*visited=0;while(p!=0||!st.empty()){while(p!=0){st.push(p);p=p->left;}p=st.top();if(p->right==0||visited==p->right){if(p->left!=0) {p->nMaxLeft=(p->left->nMaxLeft>p->left->nMaxRight?p->left->nMaxLeft:p->left->nMaxRight)+1;}if(p->right!=0){p->nMaxRight=(p->right->nMaxLeft>p->right->nMaxRight?p->right->nMaxLeft:p->right->nMaxRight)+1;}if(p->nMaxLeft+p->nMaxRight>maxLen)maxLen=p->nMaxLeft+p->nMaxRight;st.pop();visited=p;p=0;}elsep=p->right;}
}

这段代码有几个缺点:

算法加入了侵入式(intrusive)的资料nMaxLeft, nMaxRight

使用了全局变量 nMaxLen。每次使用要额外初始化。而且就算是不同的独立资料，也不能在多个线程使用这个函数

逻辑比较复杂，也有许多 NULL 相关的条件测试。

一种不改变树本身结构的方法:

我认为这个问题的核心是，情况A 及 B 需要不同的信息: A 需要子树的最大深度，B 需要子树的最大距离。只要函数能在一个节点同时计算及传回这两个信息，代码就可以很简单:

struct RESULT{int nMaxDistance;int nMaxDepth;
};
RESULT findMaxLength3(Node* root){if(root==0){RESULT empty={0,-1};return empty;}RESULT lhs=findMaxLength3(root->left);RESULT rhs=findMaxLength3(root->right);RESULT res;res.nMaxDepth=max(lhs.nMaxDepth,rhs.nMaxDepth)+1;res.nMaxDistance=max(max(lhs.nMaxDistance,rhs.nMaxDistance),lhs.nMaxDepth+rhs.nMaxDepth+2);return res;
}void postorder(Node* root){stack<Node*> st;Node* p=root,*visited=0;while(p!=0||!st.empty()){while(p!=0){st.push(p);p=p->left;}p=st.top();if(p->right==0||visited==p->right){cout<<(int)p->data<<' ';st.pop();visited=p;p=0;}else{p=p->right;}}cout<<endl;
}

计算 result 的代码很清楚；nMaxDepth 就是左子树和右子树的深度加1；nMaxDistance 则取 A 和 B 情况的最大值。

为了减少 NULL 的条件测试，进入函数时，如果节点为 NULL，会传回一个 empty 变量。比较奇怪的是 empty.nMaxDepth = -1，目的是让调用方 +1 后，把当前的不存在的 (NULL) 子树当成最大深度为 0。

除了提高了可读性，这个解法的另一个优点是减少了 O(节点数目) 大小的侵入式资料，而改为使用 O(树的最大深度) 大小的栈空间。这个设计使函数完全没有副作用(side effect)。

测试代码如下:

Node* initTree()  
{  Node* tree[10];  for(int i=0;i<10;i++)  {  tree[i]=(Node*)malloc(sizeof(Node));  tree[i]->nMaxLeft=0;  tree[i]->nMaxRight=0;  tree[i]->left=NULL;  tree[i]->right=NULL;  tree[i]->data=(char)i;  }  for(int i=0;i<=2;i++)  {  tree[i]->left=tree[2*i+1];  tree[i]->right=tree[2*i+2];  }  tree[3]->left=tree[7];  tree[5]->right=tree[8];  return tree[0];  
}  
int main(){findMaxLength(initTree());  printf("递归法:%d\n",maxLen); maxLen=0;findMaxLength2(initTree());  printf("非递归:%d\n",maxLen);  maxLen=0;RESULT r=findMaxLength3(initTree());printf("new Method:%d\n",r.nMaxDistance);
}

参考: http://blog.csdn.net/zuiaituantuan/article/details/6210317

http://www.cnblogs.com/miloyip/archive/2010/02/25/1673114.html

3.9 重建二叉树

主要是给出前序和中序或中序和后序来构造出二叉树.

这种题一般有二种形式，共同点是都已知中序序列。如果没有中序序列，是无法唯一确定一棵树的，证明略。

一、已知二叉树的前序序列和中序序列，求解树。

1、确定树的根节点。树根是当前树中所有元素在前序遍历中最先出现的元素。

2、求解树的子树。找出根节点在中序遍历中的位置，根左边的所有元素就是左子树，根右边的所有元素就是右子树。若根节点左边或右边为空，则该方向子树为空；若根节点左边和右边都为空，则根节点已经为叶子节点。

3、递归求解树。将左子树和右子树分别看成一棵二叉树，重复1、2、3步，直到所有的节点完成定位。

二、已知二叉树的后序序列和中序序列，求解树。

1、确定树的根。树根是当前树中所有元素在后序遍历中最后出现的元素。

3、递归求解树。将左子树和右子树分别看成一棵二叉树，重复1、2、3步，直到所有的节点完成定位。

举例说明：根据已知求解二叉树

中序序列 HLDBEKAFCG

后序序列 LHDKEBFGCA

1、在后序序列LHDKEBFGCA中最后出现的元素为A，HLDBEK|A|FCG

2、在后序序列LHDKEB中最后出现的元素为B，HLD|B|EK|A|FCG

3、在后序序列LHD中最后出现的元素为D，HL|D|B|EK|A|FCG

4、在后序序列LH中最后出现的元素为H，H|L|D|B|EK|A|FCG

5、在后序序列KE中最后出现的元素为E，H|L|D|B|E|K|A|FCG

5、在后序序列FGC中最后出现的元素为C，H|L|D|B|E|K|A|F|C|G

6、所有元素都已经定位，二叉树求解完成。

/ \

B C

/ \ / \

D E F G

/ \

H K

下面的代码中也包括了根据两个遍历结果输出另一个结果.

#if 0
//查找根节点的位置
char* find_root(char *start,char *end,char c){while(start<=end){if(*start==c)return start;start++;}return NULL;
}
//根据前序和中序来输出后序：核心函数
void pre_in_post_(char *pre_start,char*pre_end,char* in_start,char *in_end){if(in_start>in_end)return;if(in_start==in_end) {printf("%c",*in_start);return ;}char c=*pre_start++;char *p=find_root(in_start,in_end,c);if(p!=NULL){int len=p-in_start;pre_in_post_(pre_start,pre_start+len-1,in_start,p-1);pre_in_post_(pre_start+len,pre_end,p+1,in_end);}printf("%c",c);
}
//调用上面的递归函数
void pre_in_post(char*pre,char *in){int len1=strlen(pre);int len2=strlen(in);char *pre_end=pre+len1-1;char *in_end=in+len2-1;pre_in_post_(pre,pre_end,in,in_end);
}
//根据后序和中序来输出前序
void post_in_pre_(char *post_start,char*post_end,char* in_start,char *in_end){if(in_start>in_end)return;if(in_start==in_end) {printf("%c",*in_start);return ;}char c=*post_end--;char *p=find_root(in_start,in_end,c);printf("%c",c);if(p!=NULL){int len=p-in_start;post_in_pre_(post_start,post_start+len-1,in_start,p-1);post_in_pre_(post_start+len,post_end,p+1,in_end);}}
//调用上面的递归函数
void post_in_pre(char*post,char *in){int len1=strlen(post);int len2=strlen(in);char *post_end=post+len1-1;char *in_end=in+len2-1;post_in_pre_(post,post_end,in,in_end);
}
//二叉树节点定义
struct Node{char data;Node* left;Node* right;Node(){};Node(char c,Node* l=0,Node* r=0):data(c),left(l),right(r){}
};
//根据前序和中序来重建二叉树
Node* rebuild_pre_in_post_(char *pre_start,char*pre_end,char* in_start,char *in_end){if(in_start>in_end)return 0;if(in_start==in_end)return new Node(*in_start);char c=*pre_start++;char *p=find_root(in_start,in_end,c);Node* r=new Node(c);if(p!=NULL){int len=p-in_start;r->left=rebuild_pre_in_post_(pre_start,pre_start+len-1,in_start,p-1);r->right=rebuild_pre_in_post_(pre_start+len,pre_end,p+1,in_end);}return r;
}
//
Node* rebuild_pre_in_post(char*pre,char *in){int len1=strlen(pre);int len2=strlen(in);char *pre_end=pre+len1-1;char *in_end=in+len2-1;Node* root=rebuild_pre_in_post_(pre,pre_end,in,in_end);return root;
}
//根据后序和中序来重建二叉树
Node* rebuild_post_in_pre_(char *post_start,char*post_end,char* in_start,char *in_end){if(in_start>in_end)return 0;if(in_start==in_end)return new Node(*in_start);char c=*post_end--;char *p=find_root(in_start,in_end,c);Node* r=new Node(c);if(p!=NULL){int len=p-in_start;r->left=rebuild_post_in_pre_(post_start,post_start+len-1,in_start,p-1);r->right=rebuild_post_in_pre_(post_start+len,post_end,p+1,in_end);}return r;
}
//
Node* rebuild_post_in_pre(char*post,char *in){int len1=strlen(post);int len2=strlen(in);char *post_end=post+len1-1;char *in_end=in+len2-1;Node* root=rebuild_post_in_pre_(post,post_end,in,in_end);return root;
}
//前序遍历函数
void PreOrder(Node* root){if(root!=0) {printf("%c ",root->data);PreOrder(root->left);PreOrder(root->right);}
}
//后序变量函数
void PostOrder(Node* root){if(root!=0) {PostOrder(root->left);PostOrder(root->right);printf("%c ",root->data);}
}
int main(){char *pre="ACBGEDF";char *in="GBCEADF";char *post="GBECFDA";pre_in_post(pre,in);printf("\n");post_in_pre(post,in);printf("\n");PreOrder(rebuild_pre_in_post(pre,in));printf("\n");PostOrder(rebuild_post_in_pre(post,in));
}#endif