红黑树插入时的自平衡

红黑树插入时的自平衡

红黑树实质上是一棵自平衡的二叉查找树，引入带颜色的节点也是为了方便在进行插入或删除操作时，如果破坏了二叉查找树的平衡性能通过一系列变换保持平衡。

红黑树的性质

  1. 每个节点要么是红色，要么是黑色
  2. 根节点必须是黑色
  3. 两个红色节点不能相连
  4. 从根节点出发到达任意叶子节点经过的黑色节点个数相同

红黑树的数据结构

红黑树实质上是一颗二叉查找树，左子树的值小于根节点的值，右子树的值大于根节点的值。

在这里插入图片描述

public class RedBlackTree {private static int BLACK = 1;private static final int RED = 0;private static Node root;private static class Node {private int color = RED;private int data;private Node left;private Node right;private Node parent;Node(int data) {this.data = data;}}
}

红黑树的插入

插入的节点默认是红色的（要不然全是黑色节点它也满足红黑树的定义，不过就没意义了）；

由于红黑树是一颗二叉查找树，所以它的插入可以使用递归（先不考虑破坏红黑树的结构）

    /*** 通过递归往红黑树中插入一个新节点* @param root 要插入的树的根节点* @param data 新节点的值*/private void insert(Node root, int data) {if(root.data > data) {if(root.left == null) {Node node = new Node(data);root.left = node;node.parent = root;} else {insert(root.left, data);}}else {if(root.right == null) {Node node = new Node(data);root.right = node;node.parent = root;} else {insert(root.right, data);}}}

调整结构

新插入节点后，可能破坏红黑树的定义，虽然红黑树的定义有四条，前两条都是确定了的，不会因为新添加节点而被破坏，只需要关注第三条就可以了（满足前三条第四条就会自然满足）

    /*** 判断插入新节点后红黑树结构是否需要变化* 根据红黑树的定义，两个红色节点不能连接* @param root 插入的新节点* @return 返回true表示插入新节点后破坏了红黑树的结构，*         需要通过旋转变色来纠正，否则不需要修改。*/private boolean checkStruct(Node root) {return root.color == RED && root.parent.color == RED;}

所以只要新插入的节点的父节点是红色，就需要调整结构。调整结构的办法有三种：

1. 变色

就是把红色变为黑色，黑色变为红色

2. 左旋

在这里插入图片描述

以节点C为轴左旋的步骤：

  1. 将C的父节点A沉下来，C升上去作为新的父节点
  2. 将原来C的左子树挂到A的右子树上
  3. 其他不变

在这里插入图片描述

        /*** 左旋*   - 旋转前的右子节点变成旋转后的父节点*   - 旋转前的父节点（轴）变为旋转后父节点的左子节点*   - 旋转前轴的右子节点的右子节点旋转后变为轴的右子节点*   - 旋转前右子节点的左子树变成旋转后左子节点的右子树*   - 其他不变* @param node 以该节点为轴旋转*/private static void leftSpin(Node node) {Node nextFather = node.right;nextFather.parent = node.parent;node.right = node.right.left;nextFather.left = node;connectParent(node, nextFather);}

3. 右旋

右旋和左旋正好相反

以B为轴右旋的步骤：

  1. 将B的父节点A沉下来，B升上去作为新的父节点
  2. 将原来B的右子树接到新的A的左子树的位置

        /*** 将变换后的树和它上面的节点连接* @param node 变换前的轴* @param nextFather 变换后的子树*/private static void connectParent(Node node, Node nextFather) {// 如果变换的是根节点，就把root赋值成变换后的节点if(node.parent != null) {if(node.parent.data > node.data) {node.parent.left = nextFather;} else {node.parent.right = nextFather;}} else {RedBlackTree.root = nextFather;}node.parent = nextFather;}        /*** 右旋*   - 旋转前的左子节点变成旋转后的父节点*   - 旋转前左子节点的右子树变成旋转后右子节点的左子树* @param node 旋转轴。*/private static void rightSpin(Node node) {Node nextFather = node.left;nextFather.parent = node.parent;node.left = node.left.right;nextFather.right = node;connectParent(node, nextFather);}

根据新插入节点位置的不同情况，节点调整有五种不同的方案：

1. 父节点和叔叔节点均为红色

如果新插入节点的父节点和叔叔节点都是红色，只需要将父节点和叔叔节点变为黑色，祖父节点变为红色即可。

如果祖父节点是根节点，祖父节点保持黑色。

ONLY_CHANGE_COLOR {/*** 适用于：*   - 父节点和叔叔节点都为红色的情况；* 具体方法：*   - 把父节点和叔叔节点的颜色变为黑色，*   - 爷爷节点的颜色变为红色*   - 如果爷爷节点为根节点，爷爷节点颜色恢复黑色* @param node 当前新修改的节点*/@Overridepublic void way(Node node) {node.parent.parent.left.color = BLACK;node.parent.parent.right.color = BLACK;if(node.parent.parent.parent != null){node.parent.parent.color = RED;}}},

2. 叔叔节点不存在或为黑色，父节点位于祖父节点的左子树

2.1 当前节点位于左子树

调整办法：

  1. 将父节点设置为黑色
  2. 经祖父节点设置为红色
  3. 对祖父节点进行右旋

 RIGHT_SPIN_CHANGE_COLOR {/*** 适用于：*   - 无叔叔节点或叔叔节点为黑色*   - 父节点位于祖父节点的左子树*   - 新节点位于父节点左子树的情况* 具体方法：*   - 将当前节点的父节点设置为黑色*   - 将当前节点的祖父节点设置为红色*   - 对祖父节点进行右旋* @param node 当前节点*/@Overridepublic void way(Node node) {node.parent.color = BLACK;node.parent.parent.color = RED;Solution.rightSpin(node.parent.parent);}},
2.2 当前节点位于右子树

如果当前节点位于右子树，需要先对它的父节点进行左旋得到2.1的情况，再按2.1进行变换

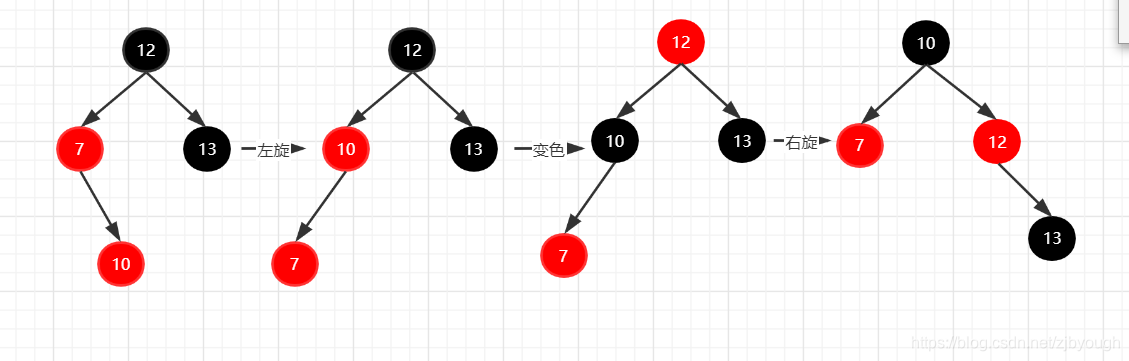
        LEFT_SPIN_WITH_RIGHT_SPIN {/*** 适用于：*   - 无叔叔节点或叔叔节点为黑色*   - 父节点位于祖父节点的左子树*   - 新节点位于父节点右子树的情况* 具体方法：*   - 对当前节点的父节点进行左旋*   - 执行 RIGHT_SPIN_CHANGE_COLOR* @param node 当前节点*/@Overridepublic void way(Node node) {Solution.leftSpin(node.parent);RIGHT_SPIN_CHANGE_COLOR.way(node.left);}},

3.叔叔节点不存在或为黑色，父节点在祖父节点的右子树

与上面的情况正好相反

3.1 当前节点位于父节点的右子树上

调整步骤：

  1. 将父节点变为黑色
  2. 将祖父节点变为红色
  3. 对祖父节点左旋

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GtHma7PH-1586137087069)(image/红黑树/image-20200406091144198.png)]

        LEFT_SPIN_CHANGE_COLOR {/*** 适用于：*   - 无叔叔节点或叔叔节点为黑色*   - 父节点位于祖父节点的右子树*   - 新节点位于父节点右子树的情况* 具体方法：*   - 将当前节点的父节点设置为黑色*   - 将当前节点的祖父节点设置为红色*   - 对祖父节点进行左旋* @param node 当前节点*/@Overridepublic void way(Node node) {node.parent.color = BLACK;node.parent.parent.color = RED;Solution.leftSpin(node.parent.parent);}},

3.2 当前节点位于左子树

调整步骤：

  1. 对当前节点的父节点进行右旋
  2. 执行3.1的步骤

        RIGHT_SPIN_LEFT_SPIN {/*** 适用于：*   - 无叔叔节点或叔叔节点为黑色*   - 父节点位于祖父节点的右子树*   - 新节点位于父节点左子树的情况* 具体方法：*   - 对当前节点的父节点进行右旋*   - 执行 LEFT_SPIN_CHANGE_COLOR* @param node 当前节点*/@Overridepublic void way(Node node) {Solution.rightSpin(node.parent);LEFT_SPIN_CHANGE_COLOR.way(node.right);}},

完整代码

package Note.cistern;public class RedBlackTree {private static int BLACK = 1;private static final int RED = 0;private static Node root;private static class Node {private int color = RED;private int data;private Node left;private Node right;private Node parent;Node(int data) {this.data = data;}@Overridepublic String toString() {return "Node{" +"data=" + data +", color=" + color +", left=" + left +", right=" + right +'}';}}interface SolutionInterface {void way(Node node);}enum Solution implements SolutionInterface{ONLY_CHANGE_COLOR {/*** 适用于：*   - 父节点和叔叔节点都为红色的情况；* 具体方法：*   - 把父节点和叔叔节点的颜色变为黑色，*   - 爷爷节点的颜色变为红色*   - 如果爷爷节点为根节点，爷爷节点颜色恢复黑色* @param node 当前新修改的节点*/@Overridepublic void way(Node node) {node.parent.parent.left.color = BLACK;node.parent.parent.right.color = BLACK;if(node.parent.parent.parent != null){node.parent.parent.color = RED;}}},RIGHT_SPIN_LEFT_SPIN {/*** 适用于：*   - 无叔叔节点或叔叔节点为黑色*   - 父节点位于祖父节点的右子树*   - 新节点位于父节点左子树的情况* 具体方法：*   - 对当前节点的父节点进行右旋*   - 执行 LEFT_SPIN_CHANGE_COLOR* @param node 当前节点*/@Overridepublic void way(Node node) {Solution.rightSpin(node.parent);LEFT_SPIN_CHANGE_COLOR.way(node.right);}},LEFT_SPIN_CHANGE_COLOR {/*** 适用于：*   - 无叔叔节点或叔叔节点为黑色*   - 父节点位于祖父节点的右子树*   - 新节点位于父节点右子树的情况* 具体方法：*   - 将当前节点的父节点设置为黑色*   - 将当前节点的祖父节点设置为红色*   - 对祖父节点进行左旋* @param node 当前节点*/@Overridepublic void way(Node node) {node.parent.color = BLACK;node.parent.parent.color = RED;Solution.leftSpin(node.parent.parent);}},LEFT_SPIN_WITH_RIGHT_SPIN {/*** 适用于：*   - 无叔叔节点或叔叔节点为黑色*   - 父节点位于祖父节点的左子树*   - 新节点位于父节点右子树的情况* 具体方法：*   - 对当前节点的父节点进行左旋*   - 执行 RIGHT_SPIN_CHANGE_COLOR* @param node 当前节点*/@Overridepublic void way(Node node) {Solution.leftSpin(node.parent);RIGHT_SPIN_CHANGE_COLOR.way(node.left);}},RIGHT_SPIN_CHANGE_COLOR {/*** 适用于：*   - 无叔叔节点或叔叔节点为黑色*   - 父节点位于祖父节点的左子树*   - 新节点位于父节点左子树的情况* 具体方法：*   - 将当前节点的父节点设置为黑色*   - 将当前节点的祖父节点设置为红色*   - 对祖父节点进行右旋* @param node 当前节点*/@Overridepublic void way(Node node) {node.parent.color = BLACK;node.parent.parent.color = RED;Solution.rightSpin(node.parent.parent);}},PASS {/*** 异常情况* @param node 当前节点*/@Overridepublic void way(Node node) {}};/*** 左旋*   - 旋转前的右子节点变成旋转后的父节点*   - 旋转前的父节点（轴）变为旋转后父节点的左子节点*   - 旋转前轴的右子节点的右子节点旋转后变为轴的右子节点*   - 旋转前右子节点的左子树变成旋转后左子节点的右子树*   - 其他不变* @param node 以该节点为轴旋转*/private static void leftSpin(Node node) {Node nextFather = node.right;nextFather.parent = node.parent;node.right = node.right.left;nextFather.left = node;connectParent(node, nextFather);}/*** 将变换后的树和它上面的节点连接* @param node 变换前的轴* @param nextFather 变换后的子树*/private static void connectParent(Node node, Node nextFather) {// 如果变换的是根节点，就把root赋值成变换后的节点if(node.parent != null) {if(node.parent.data > node.data) {node.parent.left = nextFather;} else {node.parent.right = nextFather;}} else {RedBlackTree.root = nextFather;}node.parent = nextFather;}/*** 右旋*   - 旋转前的左子节点变成旋转后的父节点*   - 旋转前左子节点的右子树变成旋转后右子节点的左子树* @param node 旋转轴。*/private static void rightSpin(Node node) {Node nextFather = node.left;nextFather.parent = node.parent;node.left = node.left.right;nextFather.right = node;connectParent(node, nextFather);}}public RedBlackTree(int rootData){root = new Node(rootData);root.color = BLACK;}/*** 通过一个整形数组快速构建红黑树* @param data 要创建树的元素*/public RedBlackTree(int [] data) {assert data.length >= 1: "data的长度至少为1";root = new Node(data[0]);root.color = BLACK;for (int i = 1; i < data.length; i++) {this.append(data[i]);}}/*** 判断插入新节点后红黑树结构是否需要变化* 根据红黑树的定义，两个红色节点不能连接* @param root 插入的新节点* @return 返回true表示插入新节点后破坏了红黑树的结构，*         需要通过旋转变色来纠正，否则不需要修改。*/private boolean checkStruct(Node root) {return root.color == RED && root.parent.color == RED;}/*** 确定该以哪种方式变换当前树，使之满足红黑树的条件* @param node 当前新加入的，使红黑树结构错误的节点* @return 返回解决办法*/private Solution determineSolution(Node node) {int fatherColor = node.parent.color;int uncleColor;// 如果父亲是爷爷的右子树if(node.parent.data > node.parent.parent.data){uncleColor = node.parent.parent.left == null? BLACK: node.parent.parent.left.color;if(fatherColor == RED && uncleColor == BLACK){if(node.data < node.parent.data){return Solution.RIGHT_SPIN_LEFT_SPIN;} else {return Solution.LEFT_SPIN_CHANGE_COLOR;}}} else {uncleColor = node.parent.parent.right == null? BLACK: node.parent.parent.right.color;if(fatherColor == RED && uncleColor == BLACK){// 插入的节点是父节点的左子节点if(node.data < node.parent.data){return Solution.RIGHT_SPIN_CHANGE_COLOR;} else {return Solution.LEFT_SPIN_WITH_RIGHT_SPIN;}}}// 如果父节点和叔叔节点都是红色if(fatherColor == RED && uncleColor == RED){return Solution.ONLY_CHANGE_COLOR;}return Solution.PASS;}private void changeTree(Node node) {Solution solution = determineSolution(node);solution.way(node);if(node.parent != null && node.parent.parent != null && checkStruct(node.parent.parent)) {changeTree(node.parent.parent);}}/*** 通过递归往红黑树中插入一个新节点* @param root 要插入的树的根节点* @param data 新节点的值*/private void insert(Node root, int data) {if(root.data > data) {if(root.left == null) {Node node = new Node(data);root.left = node;node.parent = root;if(checkStruct(node)) {changeTree(node);}} else {insert(root.left, data);}}else {if(root.right == null) {Node node = new Node(data);root.right = node;node.parent = root;if(checkStruct(node)) {changeTree(node);}} else {insert(root.right, data);}}}public Node append(int data) {insert(root, data);return root;}public Node append(int[] data) {for (int datum : data) {append(datum);}return root;}public Node getRoot(){return root;}public static void main(String[] args) {int[] data = {16, 8, 11, 13, 15, 17, 22, 25, 27};RedBlackTree redBlackTree = new RedBlackTree(data);System.out.println(redBlackTree.getRoot());}}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/457476.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

说一下自己对于 Linux 哲学的理解

说一下自己对于 Linux 哲学的理解

查阅了一些资料&#xff0c;官方的哲学思想貌似是&#xff1a; 一切皆文件由众多单一目的的小程序&#xff0c;一个程序只实现一个功能&#xff0c;多个程序组合完成复杂任务文本文件保存配置信息尽量避免与用户交互什么&#xff0c;你问我的理解&#xff1f;哲学思想&#xff…
阅读更多...
UWP学习记录

UWP学习记录

微软{X:Bind}、{Binding}资料网站 &#xff1a; https://msdn.microsoft.com/windows/uwp/xaml-platform/x-bind-markup-extension在View的ItemTemplate中绑定ViewModel的方法&#xff1a;1 <ItemsControl Name"XX" ItemsSource"{x:Bind VM.XXModels,ModeOne…
阅读更多...
dw1000信标码_DW1000方案工牌型UWB标签，助力10厘米高精度室内定位！

dw1000信标码_DW1000方案工牌型UWB标签，助力10厘米高精度室内定位！

DW1000方案工牌型UWB标签&#xff0c;助力10厘米高精度室内定位&#xff01;发布日期&#xff1a;2019-04-01 浏览次数&#xff1a;244次微能信息(95power)推出一款工牌型UWB标签VDU1510 &#xff0c;广泛应用于超宽带UWB定位系统&#xff0c;最高可实现10cm高精度人员定位。工…
阅读更多...
【Java】HashMap源码（1.7）

【Java】HashMap源码（1.7）

Life is not a ridiculous number of life, the meaning of life lies in life itself HashMap源码 散列集 数组和链表可以保持元素插入的顺序&#xff0c;对数组来说&#xff0c;他的优点是拥有连续的存储空间&#xff0c;因此可以使用元素下标快速访问&#xff0c;但缺点在…
阅读更多...
Docker 基本用法

Docker 基本用法

1.安装&#xff1a; wget http://mirrors.yun-idc.com/epel/6/i386/epel-release-6-8.noarch.rpm rpm -ivh epel-release-6-8.noarch.rpm yum install docker-io -y2.获取镜像 pull docker pull ubuntu docker pull ubuntu:14.043.运行这个镜像&#xff0c;在其中运行bash应用…
阅读更多...
画刷的使用

画刷的使用

1.画刷的定义&#xff1a; HBRUSH hBrush; windows 自定义的画刷&#xff1a; WHITE_BRUSH、LTGRAY_BRUSH、GRAY_BRUSH、DKGRAY_BRUSH、BLACK_BRUSH和NULL_BRUSH &#xff08;也叫HOLLOW_BRUSH&#xff09; 获取方法如下&#xff1a; hBrush (HBRUSH) GetStockObject (GRAY_BR…
阅读更多...
dataframe 控对象_iOS知识 - 常用小技巧大杂烩

dataframe 控对象_iOS知识 - 常用小技巧大杂烩

1&#xff0c;打印View所有子视图po [[self view]recursiveDescription]2&#xff0c;layoutSubviews调用的调用时机* 当视图第一次显示的时候会被调用。* 添加子视图也会调用这个方法。* 当本视图的大小发生改变的时候是会调用的。* 当子视图的frame发生改变的时候是会调用的。…
阅读更多...
【Java】jdk 1.8 新特性——Lambda表达式

【Java】jdk 1.8 新特性——Lambda表达式

Lambda表达式 jdk 1.8 新加入的特性&#xff0c;简化了简单接口的实现 函数式接口 函数式中只有一个待实现的方法&#xff0c;可以使用FunctionalInterface注解标注函数式接口.这个接口中只能有一个待实现的方法&#xff0c;但可以包含默认方法&#xff0c;静态方法以及Obje…
阅读更多...
【Todo】Java8新特性学习

【Todo】Java8新特性学习

参考这篇文章吧&#xff1a; http://blog.csdn.net/vchen_hao/article/details/53301073 还有一个系列转载于:https://www.cnblogs.com/charlesblc/p/6123380.html
阅读更多...
jsp调整字体大小font_html font标签如何设置字体大小？

jsp调整字体大小font_html font标签如何设置字体大小？

首先我们先来看看htmlfont标签是如何来设置字体大小的&#xff1a;都只到htmlfont标签是个专门用来设置字体的标签&#xff0c;虽然在html5中用的会很少(因为都用css样式来设置font标签里面的属性)&#xff0c;但是个人觉得font标签还是相当强大的标签的&#xff0c;为什么这么…
阅读更多...
runtime官方文档

runtime官方文档

OC是一种面向对象的动态语言&#xff0c;作为初学者可能大多数人对面向对象这个概念理解的比较深&#xff0c;而对OC是动态语言这一特性了解的比较少。那么什么是动态语言&#xff1f;动态语言就是在运行时来执行静态语言的编译链接的工作。这就要求除了编译器之外还要有一种运…
阅读更多...
【Java】synchronized关键字笔记

【Java】synchronized关键字笔记

Java Synchronized 关键字 壹. Java并发编程存在的问题 1. 可见性问题 可见性问题是指一个线程不能立刻拿到另外一个线程对共享变量的修改的结果。 如&#xff1a; package Note.concurrency;public class Demo07 {private static boolean s true;public static void mai…
阅读更多...
sql语句分析是否走索引_MySql 的SQL执行计划查看，判断是否走索引

sql语句分析是否走索引_MySql 的SQL执行计划查看，判断是否走索引

在select窗口中&#xff0c;执行以下语句&#xff1a;set profiling 1; -- 打开profile分析工具show variables like %profil%; -- 查看是否生效show processlist; -- 查看进程use cmc; -- 选择数据库show PROFILE all; -- 全部分析的类型show index from t_log_account; ##查看…
阅读更多...
SQL Server-数据类型（七）

SQL Server-数据类型（七）

前言 前面几篇文章我们讲解了索引有关知识&#xff0c;这一节我们再继续我们下面内容讲解&#xff0c;简短的内容&#xff0c;深入的理解&#xff0c;Always to review the basics。 数据类型 SQL Server支持两种字符数据类型&#xff0c;一种是常规&#xff0c;另外一种则是Un…
阅读更多...
【随记】SQL Server连接字符串参数说明

【随记】SQL Server连接字符串参数说明

废话不多说&#xff0c;请参见 SqlConnection.ConnectionString 。 转载于:https://www.cnblogs.com/xiesong/p/5749037.html
阅读更多...
【设计模式 00】设计模式的六大原则

【设计模式 00】设计模式的六大原则

设计模式的六大原则 参考&#xff1a; 设计模式六大原则 1. 单一职责原则 一个类只负责一个明确的功能 优点&#xff1a; 降低类的复杂度&#xff0c;提高代码可读性和可维护性降低变更时对其他功能的影响 2. 里氏替换原则 **原则一&#xff1a;**若 o1 是 C1 的一个实例化…
阅读更多...
pb retrieve时停止工作_大佬们挂在嘴边的PE、PB是什么？

pb retrieve时停止工作_大佬们挂在嘴边的PE、PB是什么？

在紧锣密鼓地准备科创50ETF的发行工作间隙&#xff0c;今天小夏先带你读懂最简单的PE、PB估值指标这两大指标。01、什么是PE&#xff08;市盈率&#xff09;PE&#xff0c;也就是市价盈利比率&#xff0c;简称市盈率。市盈率是指股票价格与每股收益&#xff08;每股收益&#x…
阅读更多...
EF CodeFirst 如何通过配置自动创建数据库当模型改变时

EF CodeFirst 如何通过配置自动创建数据库当模型改变时

最近悟出来一个道理&#xff0c;在这儿分享给大家&#xff1a;学历代表你的过去&#xff0c;能力代表你的现在&#xff0c;学习代表你的将来。 十年河东十年河西&#xff0c;莫欺少年穷 学无止境&#xff0c;精益求精 本篇为进阶篇&#xff0c;也是弥补自己之前没搞明白的地方,…
阅读更多...
对AutoIt中控件和窗口的理解

对AutoIt中控件和窗口的理解

经过尝试&#xff0c;对AutoIt中Control和Window有了新的认识&#xff0c;分享一下 1.Control 现在我想对一个WinForm架构的应用程序进行自动化操作&#xff0c;得到控件Advanced Mode属性为[Name:XXX]。 然而在该窗口中有多个相同属性的Control&#xff0c;而依该属性只能操作…
阅读更多...
【设计模式 01】简单工厂模式（Simple factory pattern）

【设计模式 01】简单工厂模式（Simple factory pattern）

简单工厂模式 可以根据参数的不同返回不同类的实例 参考&#xff1a; CSDN|简单工厂模式 简单工厂通过传给工厂类的参数的不同&#xff0c;返回不同的对象&#xff0c;包括三部分组成&#xff1a; 具体的”产品“工厂类&#xff08;实例化并返回”产品“&#xff09;客户端&am…
阅读更多...
最新文章

Copyright @ 2022~2023