权限之浅理解

白马过隙，在感叹时光流逝的同时不得不承认在学习中随着知识面的不断扩展所接受的东西也越来越多，尤其是那些外形比较容易混淆的命令，着实让作为新手的吃了很多苦头，趁着学习紧张之时偷个懒整理这周易混淆的命令：

chgrp （Change group):改变文件或目录所属的用户组。

chown（change owner）：改变文件的所属主和所属组。

chmod（change mode）：变更文件或目录的权限。

（下划线备注）：本人建议在接触命令时最好清楚是哪些单词的缩写，这样有利于更快的明白该命令的用法。

①chgrp

语法：

chgrp【选项】【属组】【文件】

选项：

-c或——changes：效果类似“-v”参数，但仅回报更改的部分；

-f或--quiet或——silent：不显示错误信息；

-h或--no-dereference：只对符号连接的文件作修改，而不是该其他任何相关文件；

-R或——recursive：递归处理，将指令目录下的所有文件及子目录一并处理；

-v或——verbose：显示指令执行过程；

参数：

组：指定新工作名称；

文件：指定要改变所属组的文件列表。多个文件或者目录之间使用空格隔开。

案例：

将/app/f1所有文件的所属组改为wang，且过程可见。

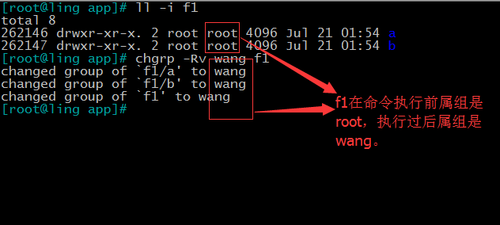
②chown

语法：

chown【选项】..【所有者】:【属组】【文件】

选项：

-c 显示更改的部分的信息

　 -f 忽略错误信息

　 -h 修复符号链接

　 -R 处理指定目录以及其子目录下的所有文件

　 -v 显示详细的处理信息

　 -deference 作用于符号链接的指向，而不是链接文件本身

参数：

用户：组：指定所有者和所属工作组。当省略“：组”，仅改变文件所有者；

文件：指定要改变所有者和工作组的文件列表。支持多个文件和目标，支持shell通配符。

案例：

修改/app/a1的所有者是magedu属组是wang。

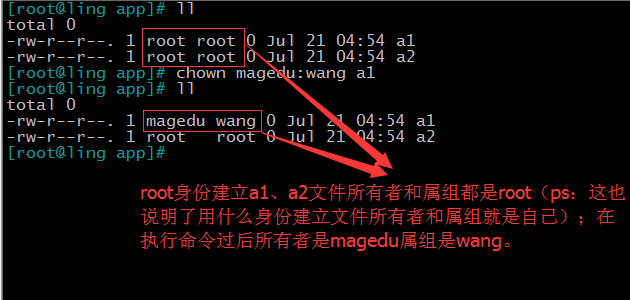
③chmod

语法：

chmod【选项】【修改权限】【文件】

选项：

-c或——changes：效果类似“-v”参数，但仅回报更改的部分；

-f或--quiet或——silent：不显示错误信息；

- R或——recursive：递归处理，将指令目录下的所有文件及子目录一并处理

-v或——verbose：显示指令执行过程

参数：

权限模式：指定文件的权限模式；

文件：要改变权限的文件。

用模式法和数字法修改/app/a1文件的权限为所有人都可以读、写、执行。

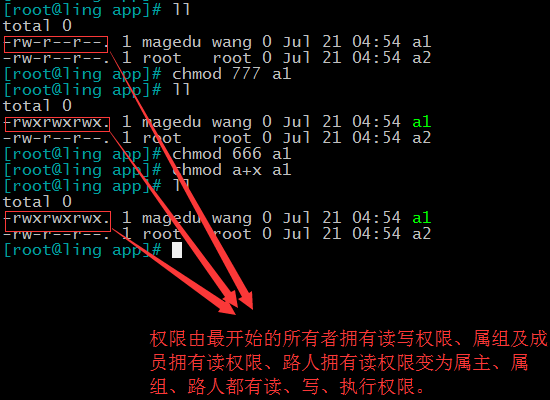
华丽的分割线

知识扩展：

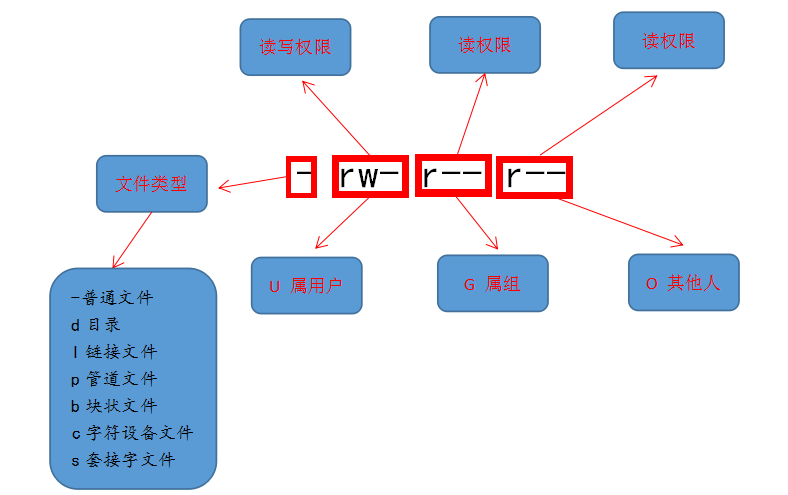
u 表示该档案的拥有者，g 表示与该档案的拥有者属于同一个群体(group)者，o 表示其他以外的人，a 表示这三者皆是。
模式法：

+表示增加权限、-表示取消权限、=表示唯一设定权限。
r表示可读取;w表示可写入;x表示可执行.

例如：①f1权限设置为所有人可读取。

chmod a+r f1

②将f1权限设置为该文件所有者可读、写、执行；属组能成员能读、写；其他人无任何权限。

chmod u+rwx,g+rw,o- f1

此外chmod也可以用数字来表示权限如 chmod 777 file
语法为：chmod abc file
其中a,b,c各为一个数字，分别表示User、Group、及Other的权限。
r=4，w=2，x=1
若要rwx属性则4+2+1=7；
若要rw-属性则4+2=6；
若要r-x属性则4+1=5。

-rw------- (600) -- 只有属主有读写权限。
-rw-r--r-- (644) -- 只有属主有读写权限；而属组用户和其他用户只有读权限。
-rwx------ (700) -- 只有属主有读、写、执行权限。
-rwxr-xr-x (755) -- 属主有读、写、执行权限；而属组用户和其他用户只有读、执行权限。
-rwx--x--x (711) -- 属主有读、写、执行权限；而属组用户和其他用户只有执行权限。
-rw-rw-rw- (666) -- 所有用户都有文件读、写权限。这种做法不可取。
-rwxrwxrwx (777) -- 所有用户都有读、写、执行权限。更不可取的做法。

提示：数字法其实与umask值相关，默认情况下管理员的umask是0022，普通用户的umask值是0002，当修改Umask值时，那么数字法有时也不会对，umask值下次再说，这次就省略啦