内存碎片
在没有其他方式辅助的情况下,我们分配给一个进程的内存是连续的。在分配时候我们需要有动态分配与碎片处理。如何理解呢?就是每个进程需要一块内存,我们要选取合适的位置的内存分配给它。当有的进程先结束了内存还给操作系统,此时可能就会产生内存碎片,要对碎片进行处理。首先对一些概念进行解释。
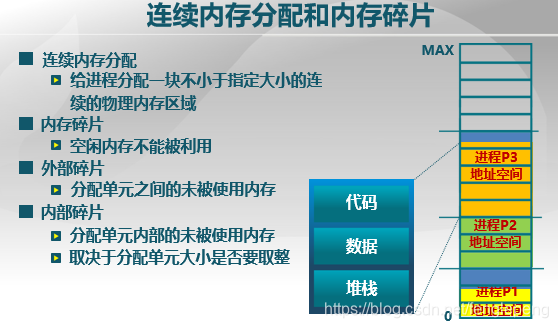
- 连续内存分配:给进程分配一块不小于指定大小的连续的物理内存区域。
- 内存碎片:不能被利用的空闲内存,内存碎片又分为外部碎片和内部碎片。
- 外部碎片:分配单元之间的未被利用的内存,比如两个进程之间的进程结束后的空间,如果后续请求的大小都大于这一部分空间,这部分空间就不能被利用,也就形成了外部碎片。
- 内部碎片:分配单元内部的未被使用的内存,这是由于分配时可能只能分配2的幂次方大小内存比如512字节,而实际使用了510字节,那么就有2字节的内部碎片。
动态分配:

当程序加载执行时,需要分配给进程一个指定大小可变的分区,分区的地址是连续的。如图中右侧分给进程1到6内存空间。当进程3和进程5结束后它们所占有的位置重新变为空闲。操作系统要维护的数据结构就包含了内存中已分配区域与未分配区域。当有新的进程请求一定的内存空间时,则根据未分配空间进行一个动态分区分配。分配的策略是多种多样的。比如:
- 最先分配,空闲分区列表按照地址顺序排序,遍历空闲分区,遇到的第一个大小满足需求的区域分配给进程。释放内存使,查看附近是否有临近的空闲区,有的话进行合并。优点是找和合并开销较小,算法简单,并且由于每次从小地址开始查找,可以在大地址处留有大块的空闲分区,可以分配给需要大内存的进程。缺点是会有外部碎片,因为切完剩下的可能有很多小块内存,也因此分配大内存时需要遍历到最后时间较长。
- 最佳匹配,空闲分区列表按照大小排序,寻找空闲区域中大小大于需求大小中最小的分配给进程,具体实现时可以对空闲分区按大小排序从最小开始寻找第一个大于需求的内存区即可,如果不排序则需要整个遍历一遍。释放时,也是与邻近空闲区域合并。而合并时我们要找的是地址邻近的而不是大小邻近的,所以合并的开销会大一些。优点大部分分配的内存尺寸较小时效果很好,因为可以避免较大的内存被拆分,同时减小外部碎片的大小,同时相对来说比较简单。缺点是外部碎片还是较多,并且越小越无法被利用,容易产生很多无用的小碎片,此外如前所述释放分区较慢,合并时算法复杂。
- 最差匹配,空闲分区列表按照大小排序,寻找空闲去榆中大小最大的区域从中划分出需要大小的内存分配给进程。释放时寻找邻近空闲分区合并。因此也存在最佳匹配的问题,释放内存时合并算法开销较大。优点是中等尺度内存分配较多时效果最好,可以避免产生太多小碎片。缺点是释放较慢,也会有外部碎片,容易破坏大的内存区域,因此后续无法分配大内存。
碎片整理
系统运行过程中,碎片越来越多,很可能无法获取需要的较大的内存空间。我们需要解决这个问题,这就是碎片整理的意义,可以通过碎片整理获得更大的连续内存空间,以便于满足进程的应用空间需求。碎片整理是通过调整进程占用的分区位置来减少或避免分区碎片的。碎片整理有很多种方式,比如碎片紧凑、分区对换。
碎片紧凑
- 实现方式:通过移动分配给进程的内存分区,以合并外部碎片。
- 条件:所有的应用程序可以动态重定位。这是因为程序中可能有很多地址引用,如果引用了绝对地址,移动分配的内存位置可能就会出错。因此需要动态重定位,执行到命令的时候才生成内存地址。
- 时机:进程处于等待状态时搬动。
- 开销:移动已分配的内存分区是有开销的,因此不会为了一小块碎片就进行紧凑。具体开销暂且按下不讲。

分区对换
分区对换是通过抢占并回收处于等待状态进程的分区,以增大可用内存空间。即将等待状态进程的数据存储到外存中,也就是对换到对换区。可以结合下面的图示理解:假设系统运行到某个时刻处于如下第一张图片的状态,图中下侧为内存与外存状态,上侧为操作系统维护的进程状态数据结构示意图,即有三个进程P1、P2、P3占满了内存区,而P1处于等待状态,P2处于运行状态,P3处于就绪状态。此时又有第四个进程要运行,而内存是不够的。则进行分区对换,对换后如第二张图所示,将处于等待状态的进程P1移动到外存,此时就有足够的内存空间。通过这种方式,我们可以让更多的进程在系统中交替进行。
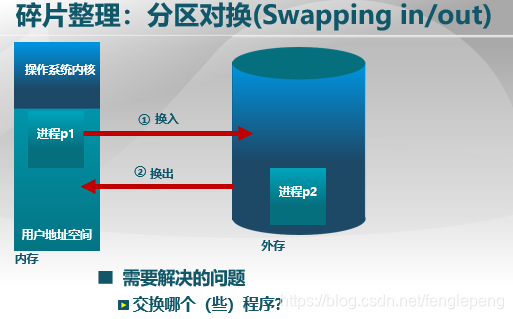
由于对换是在内存与外存之间,对换速度是非常慢的,开销很大,因此需要解决一个问题,就是到底要交换哪些进程。
伙伴系统

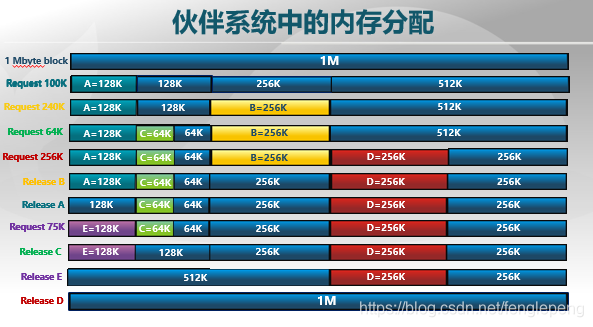
伙伴系统是连续存储分配的一种办法。它比较好地折中了分配和回收过程中分配块的位置碎片和合并的问题。伙伴系统地概念如下图:整个可分配分区大小为2的幂次方,当需要的内存空间大于当前块的一半的时候就将整个分区分配给进程,如果小于当前分区的一半,就将当前分区对半分开,将其中一半继续与需要的内存大小进行比较,递归进行下去,直到满足所需内存大小大于分区一半。可以看到这种分配方式内部碎片最大为分区大小的一半减一。知道了伙伴系统的思想,下面我们看下具体实现。
伙伴系统的实现
数据结构:
- 空闲块按大小和起始位置组织称二维数组;
- 初始状态时,只有一个大小为
的空闲块;
分配过程:
- 由小到大在空闲块数组中找最小的可用空闲块;
- 如果空闲块过大,对可用空闲块进行二等分,一个放入空闲块列表,另一块继续比较,直到得到合适的可用空闲块
分配示例:
释放过程:
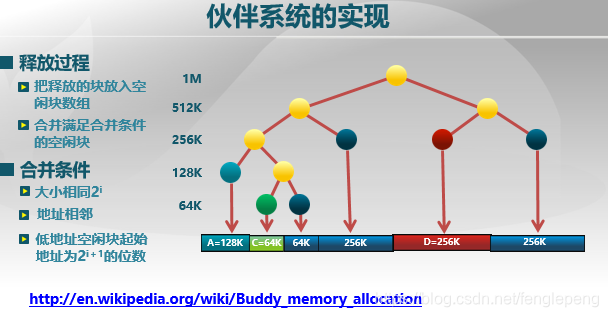
- 把释放的块放入空闲块数组
- 合并满足合并条件的空闲块
合并条件:
- 大小相同
- 地址相邻
- 起始地址小的块的地址必须是
的倍数。看起来有点抽象,其实就是地址较小的块的起始地址必须是要合并的块的大小的两倍的倍数。因此上图中三个256只有后面两个可以合并。




:非连续内存分配 段式、页式、段页式存储管理)



:虚拟存储、覆盖、交换)

)

:置换算法)
)

:进程和线程)



