又要考试了，推导一下方差最大化与均方差最小化，老师上课讲了一些均方差最小化，推导的过程很详细不过自己没有记下来，复习的时候再推一遍加深印象。感谢 @耳东陈 老师的精彩课件！

一、方差的定义

去除均值，方便计算

将均值为0后，方差就可以表示成元素平方和除以个数，即

二、协方差的定义

由于均值为 0，所以我们的协方差公式可以表示为：

三、协方差矩阵

将和变量拼成一个矩阵

那么计算协方差矩阵

顺便说一下,的期望也就是它与它自身的协方差，记为

四、方差最大化

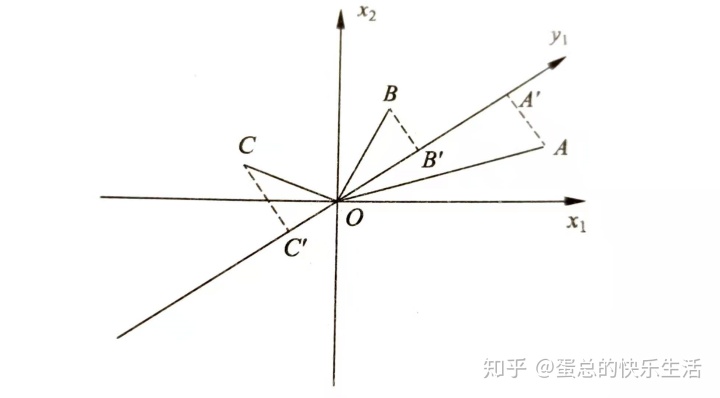
• 假设原来有两个变量x1,x2,三个样本点分别为ABC，样本分布在由轴x1x2组成的坐标系中。
• 对坐标系进行旋转变换，得到新的坐标轴y1，表示新的变量y1
• 样本点ABC在y1轴上投影，得到轴的坐标值为
• 坐标轴的平方和
  为表示样本在变量y1上的方差和
• 主成分分析旨在选取正交变换中方差最大的变量，作为第一主成分，也就是旋转变换中坐标值平方和最大的轴
• 而我们知道，对于样本而言，本身的
  为固有值，不变
• 因此可以通过勾股定理知道，方差最大
  最大等价于样本点到轴的距离
  最小

基于PCA的线性结合的第一个主成分为

那么最大化方差为

而经过了去掉均值化后，期望为0

去均值化期望为0的具体步骤如下，假设为未去除均值的情况，均值为

那么回到(9)式，继续计算这个方差，有两种理解办法，过程是一样的

• 第一种根据方差与期望的关系，通过(10)(11)算式推得到从而最大化方差等价于最大化
• 第二种根据(2)的算式，期望为0，得到以下形式，结果是相同的

最后得到的最优化问题是

五、均方误差最小化(MSE)

在方差最大化的图中，(勾股定理)可以知道Variance+MSE=定值，因此二者是等价的，换一种思路通过均方误差最小化进行推导。

向量的投影

以该图的B点为例，设B点的坐标为x1,x2,其所代表的向量为

,由于

,那么可以同样表示出直线的

,（注：由于该直线过原点就没有写截距项1）那么先算向量和向量的夹角

.

由于

,即

,可以继续化简为：

那么OB'的长度为

OB'的方向为

因此OB'的向量为

在这个部分，我们的目标是最小化均方误差，也就是

下一步就是表示出

,由向量的知识，（方向换一下没事，因为还要平方）可以得到

因此目标为

由于协方差

是定值，因此

越大，均方误差越小。

即得到的最优化问题为：

六、求解最优化问题

根据拉格朗日方程：

那么对w求导可以得到

因此代入后有

即寻找最大的特征值即为所求。

那么从大到小排列

，便得到了各个主成分。

高维小样本数据集的PCA方法预降维度方法及相关公式

• 例如:
• 这意味着在n很大的情况下，
  ，协方差矩阵太大并且不可逆很难分解
• 因此要采用预处理降维度的办法