斯特林公式是一条用来取n阶乘近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特灵公式十分好用,而且,即使在
n很小的时候,斯特灵公式的取值已经十分准确。
公式为: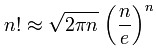
以下等式或者不等式均可以用数学归纳法予以证明!
1 + 3 + 5 + ... + (2n - 1) = n^2
1*2 + 2*3 + 3*4 + ... + n*(n + 1) = n*(n + 1)*(n + 2) / 3
1*1! + 2*2! + 3*3! + ... + n*n! = (n + 1)! - 1
1^2 + 2^2 + 3^2 + ... + n^2 = n*(n + 1)*(2n + 1) / 6
1^2 - 2^2 + 3^2 -... + (-1)^n * n^2 = (-1)^(n + 1) * n * (n + 1) / 2
2^2 + 4^2 + ... + (2n)^2 = 2n*(n+1)*(2n+1) / 3
1/2! + 2/3! + ... + n/(n+1)! = 1 - 1/(n+1)!
2^(n + 1) < 1 + (n + 1)2^n
1^3 + 2^3 + 3^3 + ... + n^3 = (n*(n + 1) / 2)^2
1/2n <= 1*3*5*...*(2n-1) / (2*4*6*...*2n) <= 1 / sqrt(n+1) n=1,2...
2^n >= n^2 , n=4, 5,...
2^n >= 2n + 1, n=3,4,...
r^0 + r^1 + ... + r^n < 1 / (1 - r), n>=0, 0<r<1
1*r^1 + 2*r^2 + ... + n*r^n < r / (1-r)^2, n>=1, 0<r<1
1/2^1 + 2/2^2 + 3/2^3 + ... + n /2^n < 2, n>=1
5^n - 1能被4整除
7^n - 1能被6整除
11^n - 6能被5整除
6*7^n - 2*3^n能被4整除
3^n + 7^n - 2能被8整除
n条直线能将平面最多划分为(n^2 + n + 2) / 2个区域
定义H(k) = 1 + 1/2 + 1/3 + ... + 1/k 则 1 + n/2 <=H(2^n) <= 1 + n
H(1) + H(2) + ... + H(n) = (n + 1) * H(n) - n
1*H(1) + 2*H(2) + ... + n*H(n) = n*(n + 1) / 2 * H(n + 1) - n * (n + 1) / 4
欧拉函数的定义:E(k)=([1,n-1]中与n互质的整数个数).因为任意正整数都可以唯一表示成如下形式:
k=p1^a1*p2^a2*……*pi^ai;(即分解质因数形式)
可以推出:E(k)=(p1-1)(p2-1)……(pi-1)*(p1^(a1-1))(p2^(a2-1))……(pi^(ai-1))
=k*(p1-1)(p2-1)……(pi-1)/(p1*p2*……pi);
=k*(1-1/p1)*(1-1/p2)....(1-1/pk)
在程序中利用欧拉函数如下性质,可以快速求出欧拉函数的值(a为N的质因素)
若(N%a==0 && (N/a)%a==0) 则有:E(N)=E(N/a)*a;
若(N%a==0 && (N/a)%a!=0) 则有:E(N)=E(N/a)*(a-1);
若N>2, 欧拉函数E(N)必定是偶数
若gcd(a,b) = 1,则有E(a * b) = E(a) * E(b)
若一个数N分解成p1^a1 * p2^a2 * ... * pn^an,那么
E(N) = p1^(a1 - 1) * (p1 - 1) * ... * pn^(an - 1) * (pn - 1)
若N>1,不大于N且与N互素的所有正整数的和是1/2 * N * E(N)
因子和: 若 k=p1^a1*p2^a2...*pi^ai F(k) = (p1^0+...+p1^a1)*(p2^0+...+p2^a2)*...*(pi^0 + ... + pi^ai)
没有一个平方数是以2,3,7,8结尾的
max{a, b, c} - min{a, b, c} = (|a - b| + |b - c| + |a - c|) / 2
ac % m = bc % m 可以得到 a % m' = b % m' m' = m / gcd(m, c)
如果a % mi = b % mi (i=1,2,...,n) 并且 l = lcm(m1, m2, ..., mn) 则可以得到 a % l = b % l
Euler 定理
若gcd(a,m)==1, 则a^(phi(m)) % m = 1 % m
Fermat小定理
p为素数,对任意的a有 a^p % p = a % p
p为素数 ,对任意的a(a<p), a^(p-1) % p = 1 % p
p为素数 , 对任意的a,若gcd(p,a)==1, a^(p-1) % p = 1 % p
一个奇数a的平方减1都是8的倍数
任意4个连续整数的乘积再加上1 一定是完全平方数
当a是整数时,a(a-1)(2a-1)是6的倍数
当a是奇数时, a(a^2 - 1)是24的倍数
n次代数方程 x^n + a1 * x^(n-1) + ... + an-1*x + an = 0 的系数都是a1, a2, ... , an都是整数。
如果它有有理数的根,证明这个根一定是整数,而且这个数一定是an的因子。如果不是整数,就一定是无理数。
设a,b都是正整数,a<b而gcd(a,b) = 1 ,如果存在一个素数p,它能够整除b,但是不能够整除10,则a/b一定不能够化成有限小数。如果b=2^a * 5^b,其中a,b都是非负整数,则a/b能化成有限小数。
设0<a<b, 且gcd(a,b) = 1, 如果a/b能表示成纯循环小数,则我们有gcd(b, 10) = 1。
设0<a<b, 且gcd(a,b) = 1, 令h是一个最小的正整数,使得10^h 与1 关于b同余,那么a/b可以表示成纯循环小数
0.d1d2d3...dh。
设b是一个正整数且gcd(10, b) = 1,令h是一个最小的正整数,能使得10^h 与1 关于b同余,则h能够整除Euler(b)
设a, b, b1都是正整数,a < b, gcd(a, b) = 1, b1 > 1, gcd(b1, 10) = 1。b = 2^c * 5^d * b1, 其中c, d都是非负整数,且不同时为0, 令h是一个最小的正整数,使得 10^h 与1 关于b1同余, 则当c>=d时,我们有a/b = 0.a1a2...aca'(c+1)...a'(c + h) ,而当c < d时,我们有a/b = 0.a1a2...ada'(d+1)...a'(d + h)
设0.a1a2...an...不能换成有限小数,也不能化成循环小数,则它不能化成分数。
设p是一个素数,m是一个正整数且m=na+b其中a是一个非负整数而b是一个不大于n-1的非负整数。令
a=p^m, 当b=0的时候,a的开n次方是一个整数,当1<= b <= n - 1时,a的开n次方不能表示为分数。
设p是一个素数,m是一个正整数且m=na+b其中a是一个非负整数而b是一个不大于n-1的非负整数。令
a=p^m, 当b=0的时候,a的开n次方是一个整数,当1<= b <= n - 1时,a的开n次方=b+c, 其中b是一个正整数而c是一个无限小数但不是循环小数。
设a是一个正整数, 当a的开n次方=b+c中b是一个正整数而0<c<1时,则a的开n次方不能表示成为分数,并且这时c是一个无限小数但不是循环小数。
(4b^3 + 3b) / (4b^2 + 1) <= b + 1 / (2b + 1/2b) <= 根号b平方+1 <= b + 1 / (2b + 1/(2b + 1 / 2b)) = (8b^4 + 8b^2 + 1) / (8b^3 + 4b)
b + 1/(2b + 1/(2b + 1/(2b + 1/2b))) <= 根号b平方+1
(16b^5 + 20b^3 + 5b) / (16b^4 + 12b^2 + 1) <= 根号b平方+1 <= (8b^4 + 8b^2 + 1) / (8b^3 + 4b)
8*8棋盘2牌的完美覆盖数目为12988816=2^4 * 901^2
一张m行n列棋盘有一个b-牌的完美覆盖,当且仅当b是m的一个因子或者b是n的一个因子
n阶幻方的幻和为 n*(n^2+1) / 2 n阶幻方体的幻和为(n^4+n) / 2
鸽巢原理: 如果n+1个物体被放进n个盒子,那么至少有一个盒子包含两个或者更多的物体
鸽巢原理加强形式: 令q1,q2,..,qn为正整数。如果将 q1+q2+...+qn-n+1 个物体放入n个盒子内,那么,至少第一个盒子至少含有q1个物体,或者第二个
盒子至少含有q2个物体,... ,或者第n个盒子至少含有qn个物体
给定m个整数a1,a2,...,am,存在整数p和q,0<=p<q<=m,使得a(p+1)+a(p+2)+...+a(m)能够被m整除。通俗的说,就是在序列a1,a2,...,am中存在连续
个a,使得这些a的和能被m整除
由n^2+1个实数构成的序列a1,a2,...,a(n^2+1)或者含有长度为n+1的递增子序列,或者含有长度为n+1的递减子序列
Ramsey定理:在6个(或更多的)人中,或者有3个人,他们中的每两个人都互相认识;或者有3个人,他们中的每两个人都彼此不认识
n个元素的集合的循环r-排列的个数由
A(n,r)/r=n!/(r * (n-r)!)给出。特别地,n个元素的循环排列的个数是(n-1)!
多重集排列:
令S是一个多重集,有k个不同类型的元素,各元素的重数分别为n1,n2,...,nk。设S的大小为n=n1+n2+...+nk。则S的排列数等于n!/(n1!*n2!*...*nk!)
多重集的组合:
令S为具有k中类型元素的一个多重集,每种元素均具有无限的重复数。则S的r-组合的个数等于 C(r+k-1,r)
如果排列P1P2...Pn有逆序列b1,b2,...,bn,且k=b1+b2+...+bn为逆序数,那么P1P2...Pn可以通过k次连续交换得到12...n
利用反射Gray码生成相邻元组1的个数相差1的所有组合
生成{1,2,...,n}的字典序r-组合的算法:
从r-组合a1a2...ar=12..r开始
当a1a2...ar不等于(n-r+1)(n-r+2)...n时,做:
i)确定最大的整数k,是的ak + 1<=n且ak + 1不等于a1,a2,...ar
ii)用r-组合 a1...a(k-1)(ak + 1)(ak+2)...(ak + r - k + 1)替换 a1a2...ar
C(n,k)=C(n-1,k)+C(n-1,k-1) 1<=k<=n-1
k * C(n,k) = n * C(n-1, k-1)
C(n,0)+C(n,1)+...+C(n,n) = 2^n C(n,0)+C(n,2)+... = 2^(n-1) C(n,1)+C(n,3)+...=2^(n-1)
1*C(n,1)+2*C(n,2)+...+n*C(n,n)=n*2^(n-1) (n>=1)
通过对等式 (1+x)^n=sigma(C(n,k)*x^k) k: 0->n 两边就微分,可以得到 sigma(k^p * C(n,k)) k: 1->n的和
sigma(C(n,k)^2) = C(2n,n) k: 1->n
C(r,0)+C(r+1,1)+...+C(r+k,k) = C(r+k+1,k)
C(0,k)+C(1,k)+...+C(n-1,k)+C(n,k)=C(n+1,k+1)
Dilworth定理: 令(X,<=)是一个有限偏序集,并令m是反链的最大大小。则X可以被划分成m个但不能再少的链
同理, 若r是链的最大大小,那么X可以被划分成r个但不能再少的反链。
卷积定理: 对任意两个长度为n的向量a和b,其中n是2的幂,
a,b的卷积等于 (DFT2n)-1(DFT2n(a) . DFT2n(b))
其中向量a和b是用0扩充使其长度达到2n,"."表示2个2n个元素组成的向量的点乘
18014398509481931 素数
18014398509482111 最小质因子为11
1637672591771101 最小质因子为6780253
中线定理(pappus定理)是指三角形ABC内BM=MC,则AB^2+AC^2=2*(AM^2+BM^2)
证明:
AC^2=AH^2+HC^2?
AB^2=AH^2+BH^2=AH^2+(HC+2MH)^2=AH^2+HC^2+4MH*HC+4MH^2
左边=AB^2+AC^2=2*AH^2+2CH^2+4MH*CH+4MH^2
右边=2*(AM^2+BM^2)=2*(AH^2+MH^2+(CH+MH)^2)=2*(AH^2+MH^2+CH^2+2CH*MH+MH^2)
得证
[modified from &豪's blog]
(1)定理:设x0,x1,x2,...是无穷实数列,xj>0,j>=1,那么,
(i)对任意的整数 n>= 1, r>=1有
<X0,...,Xn-1,Xn,...,Xn+r> = <X0,...,Xn-1,<Xn,...,Xn+r>>
= <X0,...,Xn-1,Xn+1/<Xn+1,...,Xn+r>>.
特别地有
<X0,...,Xn-1,Xn,Xn+1> = <X0,...,Xn-1,Xn+1/Xn+1>
注:用该定理可以求连分数的值
(2)对于连分数数数列 <X0,...Xn> 有递推关系:
Pn = XnPn-1+Pn-2;
Qn = XnQn-1+Qn-2;
定义: P-2 = 0; P-1 = 1; Q-2 = 1; Q-1 = 0;
所以: P0 = X0; Q0 = 1; P1 = X1X0+1; Q1 = X1;
特别地:当 Xi=1 时, {Pn}, {Qn}为Fbi数列
(3)对于连分数数数列 <X0,...Xn>
当n>= 1时,我们有PkQk-1 = Pk-1Qk = (-1)^k
当n>=2时, 我们有PkQk-2 = Pk-2Qk = (-1)^(k - 1) * xk
(4) 所有有理数都可以表示成有限连分数
(5)pell方程: x^2+ny^2=+-1的解法:
若n是平方数,则无解, 否则:
先求出sqrt(n)的连分数序列<x0,x1..xn> 其中xn = 2*x0;
对于 x^2+ny^2=-1
若n为奇数,则 x=Pn-1, y=Qn-1; n为偶数时无解
对于 x^2+ny^2=1
若n为偶数,则 x=Pn-1, y=Qn-1; n为奇数时x=P2n-1, y=Q2n-1
注:以上说的解均为最小正解
转自https://blog.csdn.net/acm_cxlove/article/details/7834776











![bind merge r 和join_[R] 制作梅西和C罗进球数的quot;追赶动画quot; - ggplot2 + gifski](https://img-blog.csdnimg.cn/img_convert/2cd9d67671878f656204bd66a45fbd3c.png)