题干：

Consider some square matrix A with side n consisting of zeros and ones. There are nrows numbered from 1 to n from top to bottom and n columns numbered from 1 to n from left to right in this matrix. We'll denote the element of the matrix which is located at the intersection of the i-row and the j-th column as Ai, j.

Let's call matrix A clear if no two cells containing ones have a common side.

Let's call matrix A symmetrical if it matches the matrices formed from it by a horizontal and/or a vertical reflection. Formally, for each pair (i, j) (1 ≤ i, j ≤ n) both of the following conditions must be met: Ai, j = An - i + 1, j and Ai, j = Ai, n - j + 1.

Let's define the sharpness of matrix A as the number of ones in it.

Given integer x, your task is to find the smallest positive integer n such that there exists a clear symmetrical matrix A with side n and sharpness x.

Input

The only line contains a single integer x (1 ≤ x ≤ 100) — the required sharpness of the matrix.

Output

Print a single number — the sought value of n.

Examples

Input

4

Output

3

Input

9

Output

5

Note

The figure below shows the matrices that correspond to the samples:

 

解题报告：

    呵呵，打表找规律，首先可以发现n为偶数一定不行（比赛时1minAC的神仙不知道是怎么看出来的）

    然后，除了3这个数，其他的都可以找个规律填数就可以了。

AC代码：

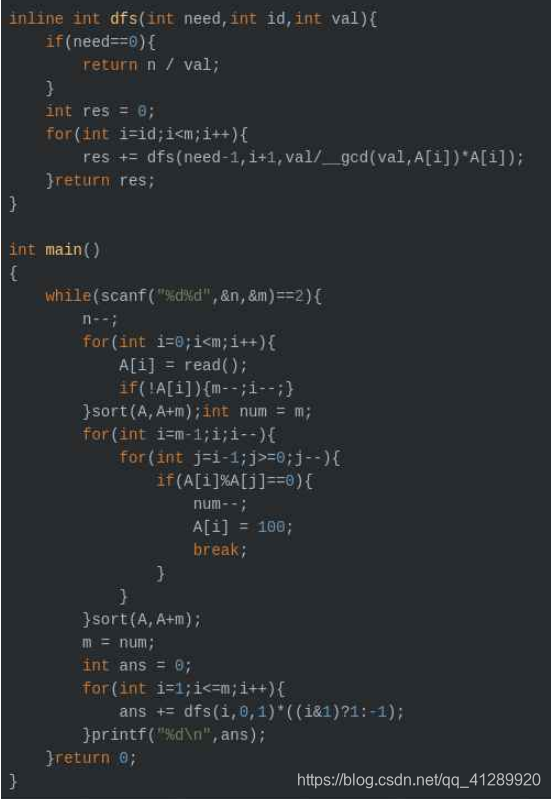
#include<iostream>
#include<algorithm>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<string>
#include<cmath>
#include<cstring>
#define ll long long
#define pb push_back
#define pm make_pair
#define fi first
#define se second
using namespace std;
const int MAX = 2e5 + 5;
ll x;
int main()
{int biao[25] = {0};cin>>x;for(int i = 1; i<=20; i++) {int now = (i+1)/2;if(i%2 == 0) biao[i] = biao[i-1];else biao[i] = now*now + (now-1)*(now-1);}
//	for(int i = 1; i<=17; i++) printf("%d\n",biao[i]);if(x== 3) printf("5\n");else printf("%d\n",lower_bound(biao+1,biao+20+1,x) - biao);return 0 ;}

 还未看懂的证明：https://blog.csdn.net/qq_24451605/article/details/48677823