10.深度学习练习：Convolutional Neural Networks: Step by Step（强烈推荐）

本文节选自吴恩达老师《深度学习专项课程》编程作业，在此表示感谢。

课程链接：https://www.deeplearning.ai/deep-learning-specialization/

1 - Packages

2 - Outline of the Assignment

3 - Convolutional Neural Networks

3.1 - Zero-Padding

3.2 - Single step of convolution

3.3 - Convolutional Neural Networks - Forward pass

4 - Pooling layer

4.1 - Forward Pooling

Welcome to Course 4's first assignment! In this assignment, you will implement convolutional (CONV) and pooling (POOL) layers in numpy, including both forward propagation and (optionally) backward propagation.

Notation:

Superscript [?] denotes an object of the $l^{th}$ layer.

Example: $a^{[4]}$ is the $4^{th}$ layer activation. $W^{[5]}$ and $b^{[5]}$ are the $5^{th}$ layer parameters

Superscript (?) denotes an object from the $i^{th}$ example.

Example: $x^{(i)}$ is the $i^{th}$ training example input.

Lowerscript ? denotes the ??ℎ entry of a vector.

Example: $a^{[l]}_i$ denotes the $i^{th}$ entry of the activations in layer ?. assuming this is a fully connected (FC) layer.

$n_H$ , $n_W$ and $n_C$ denote respectively the height, width and number of channels of a given layer. If you want to reference a specific layer ?, you can also write $n^{[l]}_H$ , $n^{[l]}_W$ , $n^{[l]}_C$ .

$n_{Hprev}$ $?_{?????}$ , $n_{Wprev}$ and $n_{Cprev}$ denote respectively the height, width and number of channels of the previous layer. If referencing a specific layer ?, this could also be denoted $n^{[l-1]}_H$ , $n^{[l-1]}_W$ , $n^{[l-1]}_C$ .

1 - Packages

import numpy as np
import h5py
import matplotlib.pyplot as plt%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'%load_ext autoreload
%autoreload 2np.random.seed(1)

2 - Outline of the Assignment

You will be implementing the building blocks of a convolutional neural network! Each function you will implement will have detailed instructions that will walk you through the steps needed:

Convolution functions, including:
- Zero Padding
- Convolve window
- Convolution forward
- Convolution backward (optional)
Pooling functions, including:
- Pooling forward
- Create mask
- Distribute value
- Pooling backward (optional)

This notebook will ask you to implement these functions from scratch in numpy. In the next notebook, you will use the TensorFlow equivalents of these functions to build the following model:

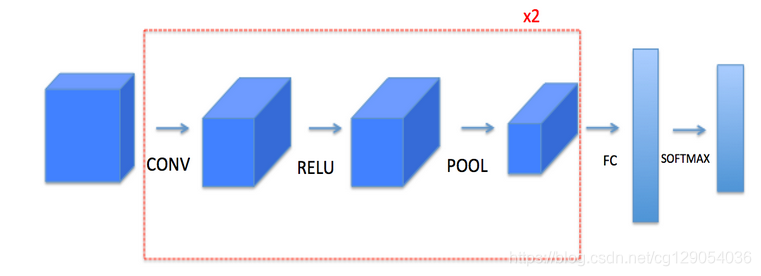
Note that for every forward function, there is its corresponding backward equivalent. Hence, at every step of your forward module you will store some parameters in a cache. These parameters are used to compute gradients during backpropagation.

3 - Convolutional Neural Networks

Although programming frameworks make convolutions easy to use, they remain one of the hardest concepts to understand in Deep Learning. A convolution layer transforms an input volume into an output volume of different size, as shown below.

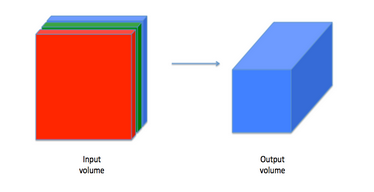
In this part, you will build every step of the convolution layer. You will first implement two helper functions: one for zero padding and the other for computing the convolution function itself.

3.1 - Zero-Padding

Zero-padding adds zeros around the border of an image:

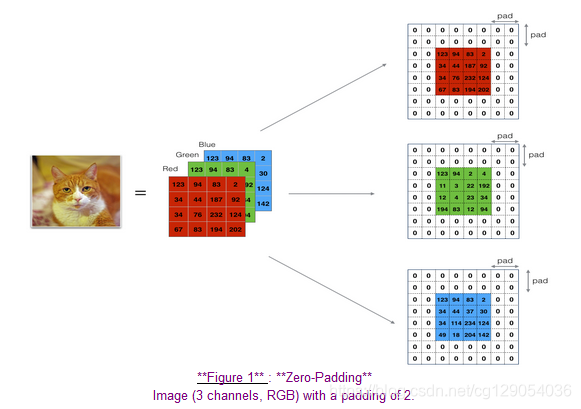
The main benefits of padding are the following:

It allows you to use a CONV layer without necessarily shrinking the height and width of the volumes. This is important for building deeper networks, since otherwise the height/width would shrink as you go to deeper layers. An important special case is the "same" convolution, in which the height/width is exactly preserved after one layer.
It helps us keep more of the information at the border of an image. Without padding, very few values at the next layer would be affected by pixels as the edges of an image.

Exercise: Implement the following function, which pads all the images of a batch of examples X with zeros. Use np.pad. Note if you want to pad the array "a" of shape (5,5,5,5,5)

with pad = 1 for the 2nd dimension, pad = 3 for the 4th dimension and pad = 0 for the rest, you would do:

a = np.pad(a, ((0,0), (1,1), (0,0), (3,3), (0,0)), 'constant', constant_values = (..,..))

# GRADED FUNCTION: zero_paddef zero_pad(X, pad):"""Pad with zeros all images of the dataset X. The padding is applied to the height and width of an image, as illustrated in Figure 1.Argument:X -- python numpy array of shape (m, n_H, n_W, n_C) representing a batch of m imagespad -- integer, amount of padding around each image on vertical and horizontal dimensionsReturns:X_pad -- padded image of shape (m, n_H + 2*pad, n_W + 2*pad, n_C)"""X_pad = np.pad(X, ((0,0), (pad, pad), (pad, pad), (0,0)), 'constant', constant_values = 0)return X_pad

3.2 - Single step of convolution

In this part, implement a single step of convolution, in which you apply the filter to a single position of the input. This will be used to build a convolutional unit, which:

Takes an input volume
Applies a filter at every position of the input
Outputs another volume (usually of different size)

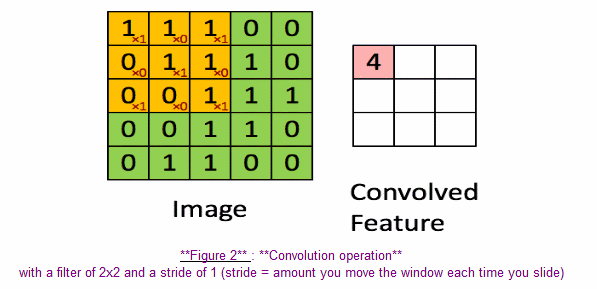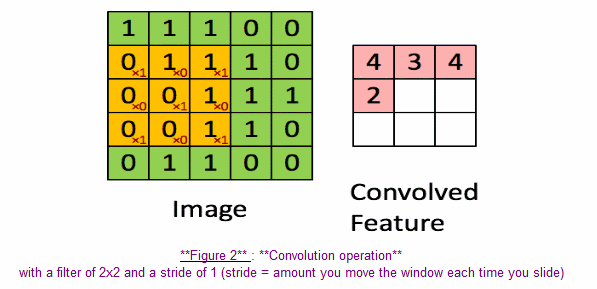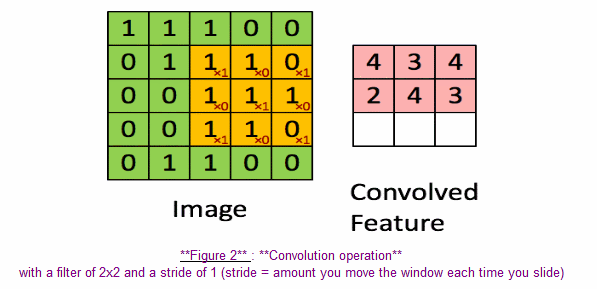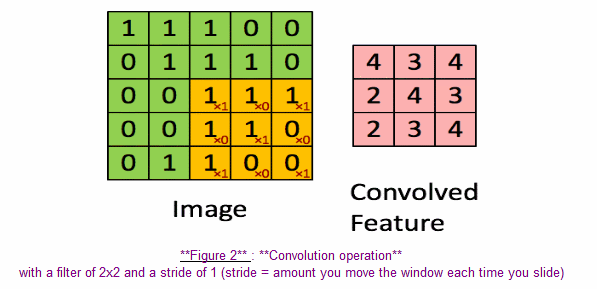
In a computer vision application, each value in the matrix on the left corresponds to a single pixel value, and we convolve a 3x3 filter with the image by multiplying its values element-wise with the original matrix, then summing them up. In this first step of the exercise, you will implement a single step of convolution, corresponding to applying a filter to just one of the positions to get a single real-valued output.

Later in this notebook, you'll apply this function to multiple positions of the input to implement the full convolutional operation.

Exercise: Implement conv_single_step(). Hint.

def conv_single_step(a_slice_prev, W, b):"""Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation of the previous layer.Arguments:a_slice_prev -- slice of input data of shape (f, f, n_C_prev)W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev)b -- Bias parameters contained in a window - matrix of shape (1, 1, 1)Returns:Z -- a scalar value, result of convolving the sliding window (W, b) on a slice x of the input data"""s = np.multiply(a_slice_prev, W) + bZ= np.sum(s)return Z

3.3 - Convolutional Neural Networks - Forward pass

In the forward pass, you will take many filters and convolve them on the input. Each 'convolution' gives you a 2D matrix output. You will then stack these outputs to get a 3D volume:

Exercise: Implement the function below to convolve the filters W on an input activation A_prev. This function takes as input A_prev, the activations output by the previous layer (for a batch of m inputs), F filters/weights denoted by W, and a bias vector denoted by b, where each filter has its own (single) bias. Finally you also have access to the hyperparameters dictionary which contains the stride and the padding.

Hint:

To select a 2x2 slice at the upper left corner of a matrix "a_prev" (shape (5,5,3)), you would do:
```
a_slice_prev = a_prev[0:2,0:2,:]
```
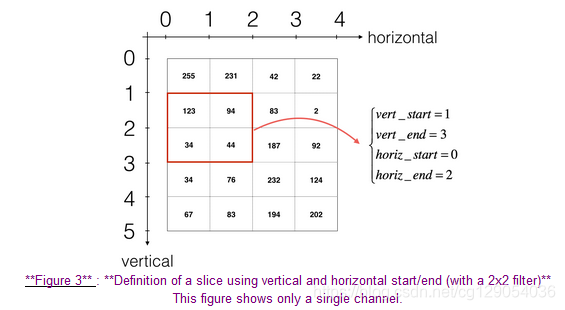
This will be useful when you will define a_slice_prev below, using the start/end indexes you will define.
To define a_slice you will need to first define its corners vert_start, vert_end, horiz_start and horiz_end. This figure may be helpful for you to find how each of the corner can be defined using h, w, f and s in the code below.

Reminder: The formulas relating the output shape of the convolution to the input shape is:

$n_H = \lfloor \frac{n_{H_{prev}} - f + 2 \times pad}{stride} \rfloor +1$

$n_W = \lfloor \frac{n_{W_{prev}} - f + 2 \times pad}{stride} \rfloor +1$

$n_C = \text{number of filters used in the convolution}$

# GRADED FUNCTION: conv_forwarddef conv_forward(A_prev, W, b, hyparameters):"""Implements the forward propagation for a convolution functionArguments:A_prev -- output activations of the previous layer, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)W -- Weights, numpy array of shape (f, f, n_C_prev, n_C)b -- Biases, numpy array of shape (1, 1, 1, n_C)hyparameters -- python dictionary containing "stride" and "pad"Returns:Z -- conv output, numpy array of shape (m, n_H, n_W, n_C)cache -- cache of values needed for the conv_backward() function"""### START CODE HERE #### Retrieve dimensions from A_prev's shape (≈1 line)  (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape# Retrieve dimensions from W's shape (≈1 line)#(f, f, n_C_prev, n_C) = W.shape(f, f, n_C_prev, n_C) = W.shape# Retrieve information from "hparameters" (≈2 lines)stride = hyparameters['stride']pad = hyparameters['pad']# Compute the dimensions of the CONV output volume using the formula given above. Hint: use int() to floor. (≈2 lines)n_H = 1 + int((n_H_prev + 2 * pad - f) / stride)n_W = 1 + int((n_W_prev + 2 * pad - f) / stride)# Initialize the output volume Z with zeros. (≈1 line)Z = np.zeros((m, n_H, n_W, n_C))# Create A_prev_pad by padding A_prevA_prev_pad = zero_pad(A_prev, pad)for i in range(m):                               # loop over the batch of training examplesa_prev_pad = A_prev_pad[i]                               # Select ith training example's padded activationfor h in range(n_H):                           # loop over vertical axis of the output volumefor w in range(n_W):                       # loop over horizontal axis of the output volumefor c in range(n_C):                   # loop over channels (= #filters) of the output volume# Find the corners of the current "slice" (≈4 lines)vert_start = h * stridevert_end = vert_start + fhoriz_start = w * stridehoriz_end = w * stride + f# Use the corners to define the (3D) slice of a_prev_pad (See Hint above the cell). (≈1 line)a_slice_prev = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]# Convolve the (3D) slice with the correct filter W and bias b, to get back one output neuron. (≈1 line)Z[i, h, w, c] = np.sum(np.multiply(a_slice_prev, W[:, :, :, c]) + b[:, :, :, c])# Making sure your output shape is correctassert(Z.shape == (m, n_H, n_W, n_C))# Save information in "cache" for the backpropcache = (A_prev, W, b, hparameters)return Z, cache

4 - Pooling layer

The pooling (POOL) layer reduces the height and width of the input. It helps reduce computation, as well as helps make feature detectors more invariant to its position in the input. The two types of pooling layers are:

Max-pooling layer: slides an (?,?) window over the input and stores the max value of the window in the output.

Average-pooling layer: slides an (?,?) window over the input and stores the average value of the window in the output.

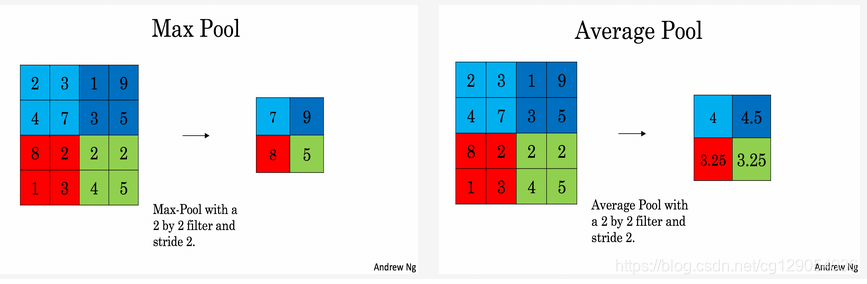
These pooling layers have no parameters for backpropagation to train. However, they have hyperparameters such as the window size ?. This specifies the height and width of the fxf window you would compute a max or average over.

4.1 - Forward Pooling

Now, you are going to implement MAX-POOL and AVG-POOL, in the same function.

Exercise: Implement the forward pass of the pooling layer. Follow the hints in the comments below.

Reminder: As there's no padding, the formulas binding the output shape of the pooling to the input shape is:

$n_H = \lfloor \frac{n_{H_{prev}} - f}{stride} \rfloor +1$

$n_W = \lfloor \frac{n_{W_{prev}} - f}{stride} \rfloor +1$

$n_C = n_{C_{prev}}$

# GRADED FUNCTION: pool_forwarddef pool_forward(A_prev, hyparameters, mode = "max"):"""Implements the forward pass of the pooling layerArguments:A_prev -- Input data, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)hyparameters -- python dictionary containing "f" and "stride"mode -- the pooling mode you would like to use, defined as a string ("max" or "average")Returns:A -- output of the pool layer, a numpy array of shape (m, n_H, n_W, n_C)cache -- cache used in the backward pass of the pooling layer, contains the input and hparameters """# Retrieve dimensions from the input shape(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape# Retrieve hyperparameters from "hparameters"f = hyparameters["f"]stride = hyparameters["stride"]# Define the dimensions of the outputn_H = int(1 + (n_H_prev - f) / stride)n_W = int(1 + (n_W_prev - f) / stride)n_C = n_C_prev# Initialize output matrix AA = np.zeros((m, n_H, n_W, n_C))              ### START CODE HERE ###for i in range(m):                         # loop over the training examplesfor h in range(n_H):                     # loop on the vertical axis of the output volumefor w in range(n_W):                 # loop on the horizontal axis of the output volumefor c in range (n_C):            # loop over the channels of the output volume# Find the corners of the current "slice" (≈4 lines)vert_start = h * stridevert_end = vert_start + fhoriz_start = w * stridehoriz_end = horiz_start + f# Use the corners to define the current slice on the ith training example of A_prev, channel c. (≈1 line)a_prev_slice = A_prev[i, vert_start:vert_end, horiz_start:horiz_end, c]# Compute the pooling operation on the slice. Use an if statment to differentiate the modes. Use np.max/np.mean.if mode == "max":A[i, h, w, c] = np.max(a_prev_slice)#A[i, h, w, c] = np.max(a_prev_slice)elif mode == "average":A[i, h, w, c] = np.mean(a_prev_slice)### END CODE HERE #### Store the input and hparameters in "cache" for pool_backward()cache = (A_prev, hyparameters)# Making sure your output shape is correctassert(A.shape == (m, n_H, n_W, n_C))return A, cache