通过这个练习可以了解到:
机器学习的典型过程:
获取数据
数据预处理
-训练模型
-应用模型
fluid训练模型的基本步骤:
配置网络结构:
定义成本函数avg_cost
定义优化器optimizer
获取训练数据
定义运算场所(place)和执行器(exe)
提供数据(feeder)
执行训练(exe.run)
预测infer()并输出拟合图像
目录
1 - 引用库
2 - 数据预处理
3 - 定义reader
4 - 训练过程
5 - 预测
1 - 引用库
首先载入需要用到的库,它们分别是:
- numpy:NumPy是Python语言的一个扩展程序库。支持高端大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。NumPy的核心功能是"ndarray"(即n-dimensional array,多维数组)数据结构。
- matplotlib.pyplot:用于生成图,在验证模型准确率和展示成本变化趋势时会使用到
- paddle.fluid:引入PaddlePaddle深度学习框架的fluid版本库;
- pandas:Pandas是python第三方库,提供高性能易用数据类型和分析工具,Pandas基于Numpy实现,常与Numpy和Matplotlib一同使用
from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import paddle
import paddle.fluid as fluidimport math
import sys#%matplotlib inline2 - 数据预处理
本次数据集使用的是2016年12月份某市某地区的房价分布。为了简化模型,假设影响房价的因素只有房屋面积,因此数据集只有两列,以txt的形式储存。
当真实数据被收集到后,它们往往不能直接使用。
例如本次数据集使用了某地区的房价分布,为了简化模型数据只有两维,并没有标出来每一列代表什么,其实分别是房屋面积与房屋价格。可以看到房价与房屋面积之间存在一种关系,这种关系究竟是什么,就是本次预测想要得到的结论。可以首先以表格的形式输出数据的前五行看一下。
colnames = ['房屋面积']+['房价']
print_data = pd.read_csv('./datasets/data.txt',names = colnames)
print_data.head()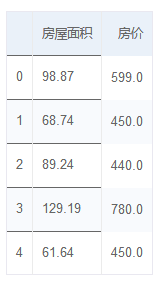
一般拿到一组数据后,第一个要处理的是数据类型不同的问题。如果各维属性中有离散值和连续值,就必须对离散值进行处理。
离散值虽然也常使用类似0、1、2这样的数字表示,但是其含义与连续值是不同的,因为这里的差值没有实际意义。例如,用0、1、2来分别表示红色、绿色和蓝色的话,并不能因此说“蓝色和红色”比“绿色和红色”的距离更远。通常对有d个可能取值的离散属性,会将它们转为d个取值为0或1的二值属性或者将每个可能取值映射为一个多维向量。
不过就这里而言,数据中没有离散值,就不用考虑这个问题了。
** 归一化 **
观察一下数据的分布特征,一般而言,如果样本有多个属性,那么各维属性的取值范围差异会很大,这就要用到一个常见的操作-归一化(normalization)了。归一化的目标是把各维属性的取值范围放缩到差不多的区间,例如[-0.5, 0.5]。这里使用一种很常见的操作方法:减掉均值,然后除以原取值范围。
# coding = utf-8 #
global x_raw,train_data,test_data
data = np.loadtxt('./datasets/data.txt',delimiter = ',')
x_raw = data.T[0].copy() #axis=0,表示按列计算
#data.shape[0]表示data中一共有多少行
maximums, minimums, avgs = data.max(axis=0), data.min(axis=0), data.sum(axis=0)/data.shape[0]
print(maximums)
print(minimums)
print(avgs)
print("the raw area :",data[:,0].max(axis = 0))#归一化,data[:,i]表示第i列的元素for i in range(data.shape[0]):data[i,0] = (data[i,0] - avgs[0]) / (maximums[0] - minimums[0])#data[i,0] = (data[i,0] - minimums[0]) / (maximums[0] - minimums[0])print('normalization:',data[:,0].max(axis = 0))基本上所有的数据在拿到后都必须进行归一化,至少有以下3条原因:
1.过大或过小的数值范围会导致计算时的浮点上溢或下溢。
2.不同的数值范围会导致不同属性对模型的重要性不同(至少在训练的初始阶段如此),而这个隐含的假设常常是不合理的。这会对优化的过程造成困难,使训练时间大大加长。
3.很多的机器学习技巧/模型(例如L1,L2正则项,向量空间模型-Vector Space Model)都基于这样的假设:所有的属性取值都差不多是以0为均值且取值范围相近的。
** 数据集分割 **
将原始数据处理为可用数据后,为了评估模型的好坏,我们将数据分成两份:训练集和测试集。
- 训练集数据用于调整模型的参数,即进行模型的训练,模型在这份数据集上的误差被称为训练误差;
- 测试集数据被用来测试,模型在这份数据集上的误差被称为测试误差。
训练模型的目的是为了通过从训练数据中找到规律来预测未知的新数据,所以测试误差是更能反映模型表现的指标。分割数据的比例要考虑到两个因素:更多的训练数据会降低参数估计的方差,从而得到更可信的模型;而更多的测试数据会降低测试误差的方差,从而得到更可信的测试误差。这个例子中设置的分割比例为8:2。
ratio = 0.8
offset = int(data.shape[0]*ratio)train_data = data[:offset]
test_data = data[offset:]print(len(data))
print(len(train_data))3 - 定义reader
构造read_data()函数,来读取训练数据集train_set或者测试数据集test_set。它的具体实现是在read_data()函数内部构造一个reader(),使用yield关键字来让reader()成为一个Generator(生成器),注意,yield关键字的作用和使用方法类似return关键字,不同之处在于yield关键字可以构造生成器(Generator)。虽然我们可以直接创建一个包含所有数据的列表,但是由于内存限制,我们不可能创建一个无限大的或者巨大的列表,并且很多时候在创建了一个百万数量级别的列表之后,却只需要用到开头的几个或几十个数据,这样造成了极大的浪费,而生成器的工作方式是在每次循环时计算下一个值,不断推算出后续的元素,不会创建完整的数据集列表,从而节约了内存使用。
def read_data(data_set):"""一个readerArgs:data_set -- 要获取的数据集Return:reader -- 用于获取训练集及其标签的生成器generator"""def reader():"""一个readerArgs:Return:data[:-1],data[-1:] --使用yield返回生成器data[:-1]表示前n-1个元素,也就是训练数据,data[-1:]表示最后一个元素,也就是对应的标签"""for data in data_set:yield data[:-1],data[-1:]return reader#测试readertest_array = ([10,100],[20,200])
print("test_array for read_data:")
for value in read_data(test_array)():print(value)接下来我们定义了用于训练的数据提供器。提供器每次读入一个大小为BATCH_SIZE的数据批次。如果用户希望加一些随机性,它可以同时定义一个批次大小和一个缓存大小。这样的话,每次数据提供器会从缓存中随机读取批次大小那么多的数据。我们都可以通过batch_size进行设置,这个大小一般是2的N次方。
关于参数的解释如下:
- paddle.reader.shuffle(read_data(train_data), buf_size=500)表示从read_data(train_data)中读取了buf_size=500大小的数据并打乱顺序
- paddle.batch(reader(), batch_size=BATCH_SIZE)表示从打乱的数据中再取出BATCH_SIZE=20大小的数据进行一次迭代训练
如果buf_size设置的数值大于数据集本身,就直接把整个数据集打乱顺序;如果buf_size设置的数值小于数据集本身,就按照buf_size的大小打乱顺序。
BATCH_SIZE = 8# 设置训练reader
train_reader = paddle.batch(paddle.reader.shuffle(read_data(train_data), buf_size=500),batch_size=BATCH_SIZE)#设置测试 reader
test_reader = paddle.batch(paddle.reader.shuffle(read_data(test_data), buf_size=500),batch_size=BATCH_SIZE)4 - 训练过程
完成了数据的预处理工作并构造了read_data()来读取数据,接下来将进入模型的训练过程,使用PaddlePaddle来定义构造可训练的线性回归模型,关键步骤如下:
配置网络结构和设置参数
- 配置网络结构
- 定义损失函数cost
- 定义执行器(参数随机初始化)
- 定义优化器optimizer
模型训练
预测
绘制拟合图像
定义运算场所:
首先进行最基本的运算场所定义,在 fluid 中使用 place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace() 来进行初始化:
- place 表示fluid program的执行设备,常见的有 fluid.CUDAPlace(0) 和 fluid.CPUPlace()
- use_cuda = False 表示不使用 GPU 进行加速训练
#使用CPU或者GPU训练
use_cuda = False
place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace() 配置网络结构和设置参数:
# 输入层,fluid.layers.data表示数据层,name=’x’:名称为x,输出类型为tensor
# shape=[1]:数据为1维向量
# dtype='float32':数据类型为float32x = fluid.layers.data(name='x', shape=[1], dtype='float32')# 标签数据,fluid.layers.data表示数据层,name=’y’:名称为y,输出类型为tensor
# shape=[1]:数据为1维向量
y = fluid.layers.data(name='y', shape=[1], dtype = 'float32')# 输出层,fluid.layers.fc表示全连接层,input=x: 该层输入数据为x
# size=1:神经元个数,act=None:激活函数为线性函数
y_predict = fluid.layers.fc(input=x, size=1, act=None)定义损失函数:
# 定义损失函数为均方差损失函数,并且求平均损失,返回值名称为avg_loss
avg_loss = fluid.layers.square_error_cost(input = y_predict, label = y)
avg_loss = fluid.layers.mean(avg_loss)定义执行器(参数随机初始化):
exe = fluid.Executor(place)配置训练程序:
main_program = fluid.default_main_program() # 获取默认/全局主函数
startup_program = fluid.default_startup_program() # 获取默认/全局启动程序#克隆main_program得到test_program
#有些operator在训练和测试之间的操作是不同的,例如batch_norm,使用参数for_test来区分该程序是用来训练还是用来测试
#该api不会删除任何操作符,请在backward和optimization之前使用
test_program = main_program.clone(for_test=True)优化方法:
# 创建optimizer,更多优化算子可以参考 fluid.optimizer()
learning_rate = 0.0005
sgd_optimizer = fluid.optimizer.SGD(learning_rate)
sgd_optimizer.minimize(avg_loss)
print("optimizer is ready")创建训练过程:
训练需要有一个训练程序和一些必要参数,并构建了一个获取训练过程中测试误差的函数。必要参数有executor,program,reader,feeder,fetch_list,executor表示之前创建的执行器,program表示执行器所执行的program,是之前创建的program,如果该项参数没有给定的话则默认使用defalut_main_program,reader表示读取到的数据,feeder表示前向输入的变量,fetch_list表示用户想得到的变量或者命名的结果。
# For training test cost
def train_test(executor, program, reader, feeder, fetch_list):accumulated = 1 * [0]count = 0for data_test in reader():outs = executor.run(program=program, feed=feeder.feed(data_test), fetch_list=fetch_list)accumulated = [x_c[0] + x_c[1][0] for x_c in zip(accumulated, outs)] # 累加测试过程中的损失值count += 1 # 累加测试集中的样本数量return [x_d / count for x_d in accumulated] # 计算平均损失#定义模型保存路径:
#params_dirname用于定义模型保存路径。
params_dirname = "easy_fit_a_line.inference.model"训练主循环:
#用于画图展示训练cost
from paddle.utils.plot import Ploter
train_prompt = "Train cost"
test_prompt = "Test cost"
plot_prompt = Ploter(train_prompt, test_prompt)
step = 0# 训练主循环
feeder = fluid.DataFeeder(place=place, feed_list=[x, y])
exe.run(startup_program)exe_test = fluid.Executor(place)#num_epochs=100表示迭代训练100次后停止训练。
num_epochs = 150for pass_id in range(num_epochs):for data_train in train_reader():avg_loss_value, = exe.run(main_program,feed=feeder.feed(data_train),fetch_list=[avg_loss])if step % 10 == 0: # 每10个批次记录并输出一下训练损失plot_prompt.append(train_prompt, step, avg_loss_value[0])plot_prompt.plot()#print("%s, Step %d, Cost %f" %(train_prompt, step, avg_loss_value[0]))if step % 100 == 0: # 每100批次记录并输出一下测试损失test_metics = train_test(executor=exe_test,program=test_program,reader=test_reader,fetch_list=[avg_loss.name],feeder=feeder)plot_prompt.append(test_prompt, step, test_metics[0])plot_prompt.plot()#print("%s, Step %d, Cost %f" %(test_prompt, step, test_metics[0]))if test_metics[0] < 10.0: # 如果准确率达到要求,则停止训练breakstep += 1if math.isnan(float(avg_loss_value[0])):sys.exit("got NaN loss, training failed.")#保存训练参数到之前给定的路径中
if params_dirname is not None:fluid.io.save_inference_model(params_dirname, ['x'], [y_predict], exe)
5 - 预测
通过fluid.io.load_inference_model,预测器会从params_dirname中读取已经训练好的模型,来对从未遇见过的数据进行预测。
print(test_metics)
infer_exe = fluid.Executor(place)
inference_scope = fluid.core.Scope()预测
预测器会从params_dirname中读取已经训练好的模型,来对从未遇见过的数据进行预测。
- tensor_x:生成batch_size个[0,1]区间的随机数,以 tensor 的格式储存
- results:预测对应 tensor_x 面积的房价结果
- raw_x:由于数据处理时我们做了归一化操作,为了更直观的判断预测是否准确,将数据进行反归一化,得到随机数对应的原始数据。
with fluid.scope_guard(inference_scope):[inference_program, feed_target_names, fetch_targets] = fluid.io.load_inference_model(params_dirname, infer_exe) # 载入预训练模型batch_size = 2tensor_x = np.random.uniform(0, 1, [batch_size, 1]).astype("float32")print("tensor_x is :" ,tensor_x )results = infer_exe.run(inference_program,feed={feed_target_names[0]: tensor_x},fetch_list=fetch_targets) # 进行预测#raw_x = tensor_x*(maximums[i]-minimums[i])+avgs[i]raw_x = tensor_x * (maximums[0] - minimums[0]) + avgs[0]#raw_x = tensor_x * (maximums[0] - minimums[0]) + minimums[0]print("the area is:",raw_x)print("infer results: ", results[0])a = (results[0][0][0] - results[0][1][0]) / (raw_x[0][0]-raw_x[1][0])
b = (results[0][0][0] - a * raw_x[0][0])
**(5)绘制拟合图像 **
通过训练,本次线性回归模型输出了一条拟合的直线,想要直观的判断模型好坏可将拟合直线与数据的图像绘制出来。
import numpy as np
import matplotlib.pyplot as pltdef plot_data(data):x = data[:,0]y = data[:,1]y_predict = x*a + bplt.scatter(x,y,marker='.',c='r',label='True')plt.title('House Price Distributions')plt.xlabel('House Area ')plt.ylabel('House Price ')plt.xlim(0,250)plt.ylim(0,2500)predict = plt.plot(x,y_predict,label='Predict')plt.legend(loc='upper left')plt.savefig('result1.png')plt.show()data = np.loadtxt('./datasets/data.txt',delimiter = ',')
plot_data(data)

)
:猫脸识别)

)
:MNIST(手写数字识别))

:迁移学习)


)


)

)

)

)