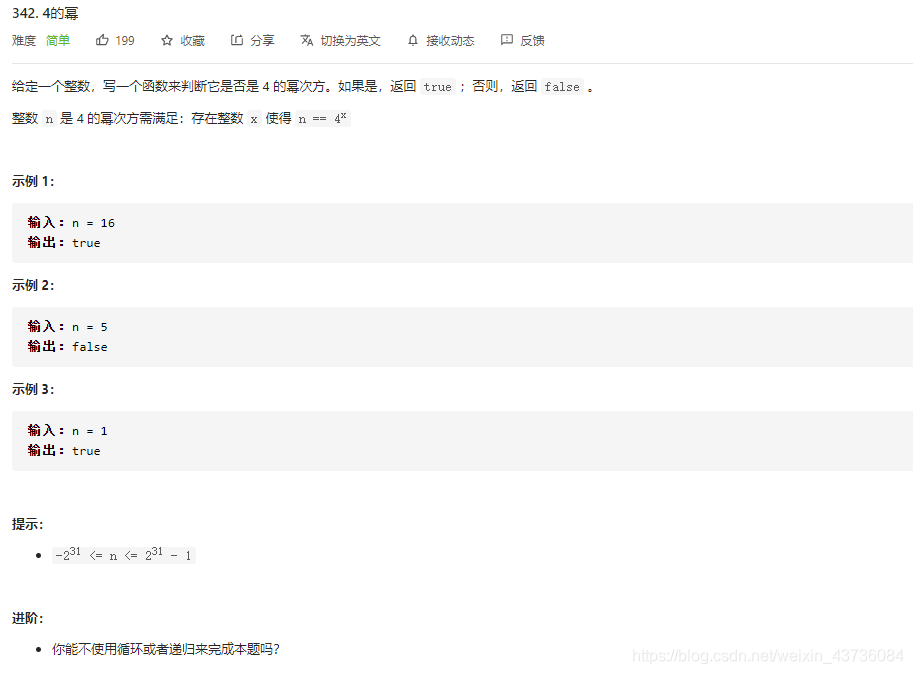
不使用循环来今天解题
public boolean isPowerOfFour(int n) {return n > 0 && (n & (n-1)) == 0 && n % 3==1;}
首先去做了2的幂这道题，并了解了n&(n-1)的过程，然后思考一下这道题:求二进制中1的个数，理解了n&(n-1)这个题就好做了。
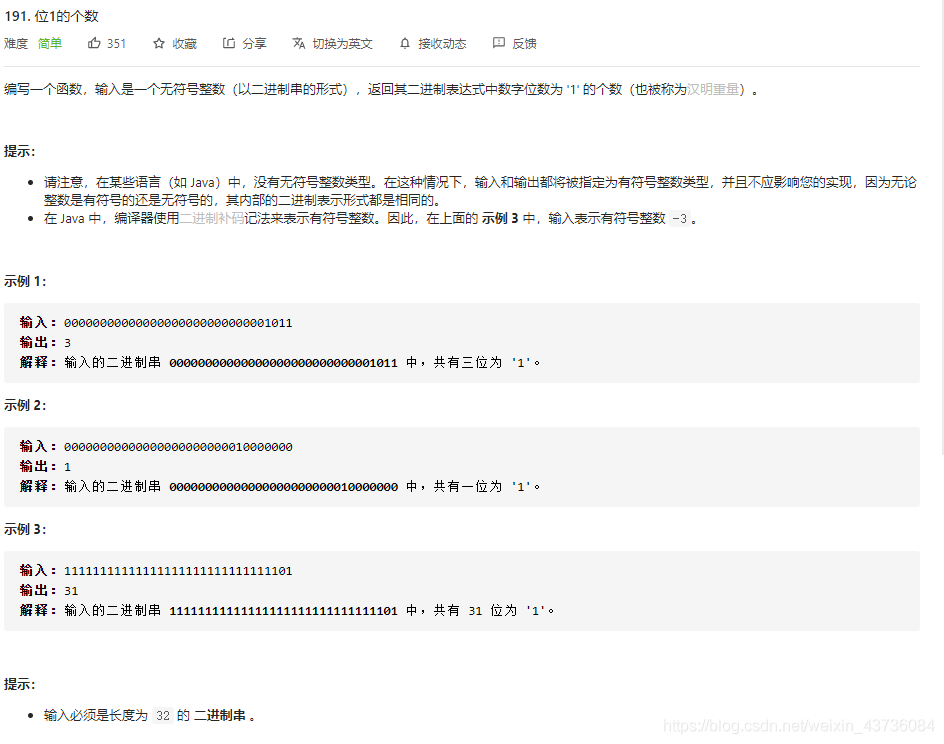
public static int xxxxx(int n) {int i = 1;while((n&(n-1)) != 0){i++;}return i;}
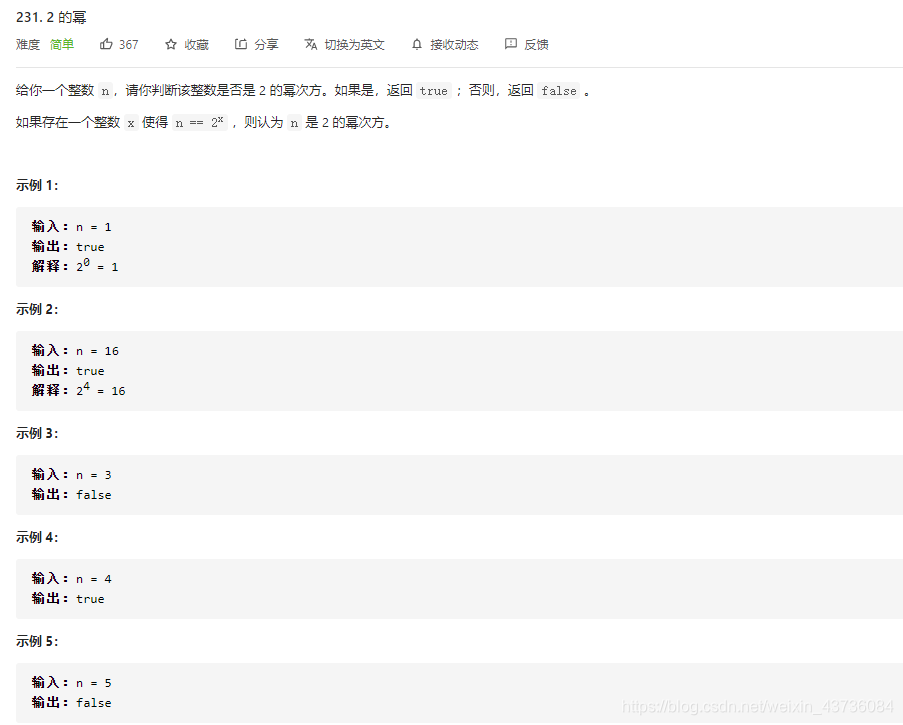
public boolean isPowerOfTwo(int n) {return n > 0 && (n & (n - 1)) == 0;}
与2的幂不同的是4的幂的位数一定是偶数个
看了下题解，如何来获取位数，但是感觉下面这个办法简单一些
如果 nn 是 44 的幂，那么它可以表示成 4^x4
x
的形式，我们可以发现它除以 33 的余数一定为 11，即：
4^x \equiv (3+1)^x \equiv 1^x \equiv 1 \quad (\bmod ~3)
4
x
≡(3+1)
x
≡1
x
≡1(mod 3)
如果 nn 是 22 的幂却不是 44 的幂，那么它可以表示成 4^x \times 24
x
×2 的形式，此时它除以 33 的余数一定为 22。
因此我们可以通过 nn 除以 33 的余数是否为 11 来判断 nn 是否是 44 的幂。
)
)
