二叉树序列化

文件的大小尽可能的小。

想了四种方法：

第一种方法：把二叉树按前序和中序遍历一遍，存两次二叉树。

第二种方法：将二叉树按左枝为0，右枝为1进行路径编码，那么每个节点都可以表示成，节点信息和路径信息进行永久化。
第三种方法：将二叉树变成满二叉树，采用数组存储满二叉树，那么数据index和根据二叉树的节点信息进行永久化。

0	1	2	3	4	5	6	7	8	9
ROOT	L	R	LL	LR	RL	RR	LLL	LLR	LRL

第四种方法：采用一个位图和所有节点信息进行存储，位图上的0代表着相应满二叉树的节点没有节点，1代表有节点信息。
四种方法比较：第一种方法，冗余信息量刚好是原有数据的两倍。
第二种方法存储的是节点信息和路径信息，冗余信息量是（路径信息*节点数）
第三种方法：冗余信息为，sizeof(unsigned int) * 节点数
第四种方法：冗余信息为树的层数K，（2^k -1）bit
因此第四种方法在二叉树是满二叉树或者二叉树的层数比较小的情况下，信息量比较小，但是在树的层比较丰富的情况下，冗余信息非常大。我觉得也不是什么特别好的方法。貌似我还是没有得到正确答案。

[html] view plaincopyprint?

#include<iostream>
#include <fstream>
#include<math.h>
#define max(a,b) ((a)>(b)?(a):(b))
using namespace std;
//随机数大小
const int NUMBER = 9;
//修改树的深度
const int DEPTH = 6;
//文件流
ofstream fout3("serialize3.txt");
ofstream fout4("serialize4.txt");
ofstream fout("tree.txt");
//树节点信息
typedef struct Node
{
int data;
Node * left;
Node * right;
} BinaryTree;
//随机生成二叉树
void generate(Node ** tree, int d)
{
*tree = (Node *)malloc(sizeof(Node));
(*tree)->data = rand()%NUMBER + 1;
int isleft = rand()%DEPTH;
if(d+isleft < DEPTH)
generate(&((*tree)->left), d+1);
else
(*tree)->left = NULL;
int isright = rand()%DEPTH;
if (d+isright < DEPTH)
{
generate(&((*tree)->right), d+1);
}
else
(*tree)->right = NULL;
}
//获取树的深度
int getTreeDepth(Node * tree)
{
if (tree == NULL)
{
return 0;
}
int left = getTreeDepth(tree->left);
int right = getTreeDepth(tree->right);
return (max( left, right ) + 1);
}
//打印第i层树
void printTreeLevel(Node * tree, int index, int level,int depth)
{
if(tree == NULL)
{
int length = pow(2.0,(depth-index))-1;
for (int i=1; i <= length; i ++)
{
fout << " ";
cout <<" ";
}
return;
}
if(index == level)
{
//左子树宽度
int length = pow(2.0,(depth-level-1))-1;
for (int j=1; j <= length; j ++)
{
fout <<" ";
cout <<" ";
}
fout << tree->data;
cout << tree->data;
//右子树宽度
for (int j=1; j <= length; j ++)
{
fout <<" ";
cout <<" ";
}
return;
}
printTreeLevel(tree->left, index +1,level, depth);
fout <<" ";
cout <<" ";
printTreeLevel(tree->right, index+1, level, depth);
}
//逐层遍历二叉树
//两种思路，一种采用广度遍历的方法，利用链表空间逐层存储，逐层打印
//一种使用递归的方法逐层打印
void printTree(Node * tree)
{
int depth = getTreeDepth(tree);
for (int i=0; i < depth; i ++)
{
printTreeLevel(tree, 0, i,depth);
fout << endl;
cout <<endl;
}
}
//序列化，四种方法
//第一种方法：把二叉树按前序和中序遍历一遍，存两次二叉树。
//第二种方法：将二叉树按左枝为0，右枝为1进行路径编码，那么每个节点都可以表示成，节点信息和路径信息进行永久化。
//第三种方法：将二叉树变成满二叉树，采用数组存储满二叉树，那么数据index和根据二叉树的节点信息进行永久化。
//第四种方法：采用一个位图和所有节点信息进行存储，位图上的0代表着相应满二叉树的节点没有节点，1代表有节点信息。
//四种方法比较：第一种方法，冗余信息量刚好是原有数据的两倍。
//第二种方法存储的是节点信息和路径信息，冗余信息量是（路径信息*节点数）
//第三种方法：冗余信息为，sizeof(unsigned int) * 节点数
//第四种方法：冗余信息为树的层数K，（2^k -1）bit
//因此第四种方法在二叉树是满二叉树或者二叉树的层数比较小的情况下，信息量比较小，但是在树的层比较丰富的情况下，
//冗余信息非常大。我觉得也不是什么特别好的方法。貌似我还是没有得到正确答案。
//第三种方法序列化
void serialize_3(Node *tree, unsigned int index)
{
if (tree == NULL)
{
return;
}
fout3 << tree->data << " " << index << endl;
serialize_3(tree->left, index*2);
serialize_3(tree->right, index*2 +1);
}
//设置bitmap
void setbitmap(Node * tree, int * map,unsigned int bit, int level)
{
if (tree == NULL)
{
return;
}
unsigned int index = bit / 32;
unsigned int b = bit%32;
map[index] = map[index] | (1<<b);
fout4 << tree->data << " ";
setbitmap(tree->left, map, bit * 2+1, level+1);
setbitmap(tree->right, map, bit * 2 +2 , level+1);
}
//第四种方法永久化
void seralize_4(Node* tree)
{
int depth = getTreeDepth(tree);
int len = (depth-5)>0? (depth-5) : 0;
len = (1<<len);
int* map = new int[len];
memset(map, 0, sizeof(int) * len);
setbitmap(tree, map, 0, 1);
fout4<<endl;
for (int i=0; i <len; i ++)
{
fout4 <<hex << map[i];
}
fout4 <<endl;
delete [] map;
}
//释放内存
void deleteTree(Node * tree)
{
if (tree == NULL)
{
return;
}
deleteTree(tree->left);
deleteTree(tree->right);
free(tree);
}
int main()
{
BinaryTree * tree=NULL;
//随机生成二叉树
cout << "随机生成二叉树，并保存到tree.txt"<<endl;
generate(&tree, 0);
//树层比较低的，打印出二叉树
if (DEPTH <= 15)
{
printTree(tree);
}
//第三种序列化方法
cout << "用第三种方法持久化到serialize3.txt" <<endl;
serialize_3(tree, 1);
//第四种序列化方法
cout <<"用第四种方法持久化到serialize4.txt" <<endl;
seralize_4(tree);
//回收空间
deleteTree(tree);
system("pause");
return 0;
}

#include<iostream>
#include <fstream>
#include<math.h>#define  max(a,b) ((a)>(b)?(a):(b))using namespace std;
//随机数大小
const int NUMBER = 9;
//修改树的深度
const int DEPTH = 6;//文件流
ofstream fout3("serialize3.txt");
ofstream fout4("serialize4.txt");
ofstream fout("tree.txt");//树节点信息
typedef struct Node
{int data;Node * left;Node * right;
} BinaryTree;//随机生成二叉树
void generate(Node ** tree, int d)
{*tree = (Node *)malloc(sizeof(Node));(*tree)->data = rand()%NUMBER + 1;int isleft = rand()%DEPTH;if(d+isleft < DEPTH)generate(&((*tree)->left), d+1);else(*tree)->left = NULL;int isright = rand()%DEPTH;if (d+isright < DEPTH){generate(&((*tree)->right), d+1);}else(*tree)->right = NULL;
}//获取树的深度
int getTreeDepth(Node * tree)
{if (tree == NULL){return 0;}int left = getTreeDepth(tree->left);int right = getTreeDepth(tree->right);return (max( left, right ) + 1);
}//打印第i层树
void printTreeLevel(Node * tree, int index, int level,int depth)
{if(tree == NULL){int length = pow(2.0,(depth-index))-1;for (int i=1; i <= length; i ++){fout << "  ";cout <<" ";}return;}if(index == level){//左子树宽度int length = pow(2.0,(depth-level-1))-1;for (int j=1; j <= length; j ++){fout <<"  ";cout <<" ";}fout << tree->data;cout << tree->data;//右子树宽度for (int j=1; j <= length; j ++){fout <<"  ";cout <<" ";}return;}printTreeLevel(tree->left, index +1,level, depth);fout <<"  ";cout <<" ";printTreeLevel(tree->right, index+1, level, depth);
}//逐层遍历二叉树
//两种思路，一种采用广度遍历的方法，利用链表空间逐层存储，逐层打印
//一种使用递归的方法逐层打印
void printTree(Node * tree)
{int depth = getTreeDepth(tree);for (int i=0; i < depth; i ++){printTreeLevel(tree, 0, i,depth);fout << endl;cout <<endl;}
}//序列化，四种方法
//第一种方法：把二叉树按前序和中序遍历一遍，存两次二叉树。
//第二种方法：将二叉树按左枝为0，右枝为1进行路径编码，那么每个节点都可以表示成，节点信息和路径信息进行永久化。
//第三种方法：将二叉树变成满二叉树，采用数组存储满二叉树，那么数据index和根据二叉树的节点信息进行永久化。
//第四种方法：采用一个位图和所有节点信息进行存储，位图上的0代表着相应满二叉树的节点没有节点，1代表有节点信息。
//四种方法比较：第一种方法，冗余信息量刚好是原有数据的两倍。
//第二种方法存储的是节点信息和路径信息，冗余信息量是（路径信息*节点数）
//第三种方法：冗余信息为，sizeof(unsigned int) * 节点数
//第四种方法：冗余信息为树的层数K，（2^k -1）bit 
//因此第四种方法在二叉树是满二叉树或者二叉树的层数比较小的情况下，信息量比较小，但是在树的层比较丰富的情况下，
//冗余信息非常大。我觉得也不是什么特别好的方法。貌似我还是没有得到正确答案。//第三种方法序列化
void serialize_3(Node *tree, unsigned int index)
{if (tree == NULL){return;}fout3 << tree->data << " " << index << endl;serialize_3(tree->left, index*2);serialize_3(tree->right, index*2 +1);
}//设置bitmap
void setbitmap(Node * tree, int * map,unsigned int bit, int level)
{if (tree == NULL){return;}unsigned int index = bit / 32;unsigned int b = bit%32;map[index] = map[index] | (1<<b);fout4 << tree->data << " ";setbitmap(tree->left, map,  bit * 2+1, level+1);setbitmap(tree->right, map, bit * 2 +2 , level+1);
}//第四种方法永久化
void seralize_4(Node* tree)
{int depth = getTreeDepth(tree);int len = (depth-5)>0? (depth-5) : 0;len = (1<<len);int* map = new int[len];memset(map, 0, sizeof(int) * len);setbitmap(tree, map, 0, 1);fout4<<endl;for (int i=0; i <len; i ++){fout4 <<hex << map[i];}fout4 <<endl;delete [] map;
}//释放内存
void deleteTree(Node * tree)
{if (tree == NULL){return;}deleteTree(tree->left);deleteTree(tree->right);free(tree);
}int main()
{BinaryTree * tree=NULL;//随机生成二叉树cout << "随机生成二叉树，并保存到tree.txt"<<endl;generate(&tree, 0);//树层比较低的，打印出二叉树if (DEPTH <= 15){printTree(tree);}//第三种序列化方法cout << "用第三种方法持久化到serialize3.txt" <<endl;serialize_3(tree, 1);//第四种序列化方法cout <<"用第四种方法持久化到serialize4.txt" <<endl;seralize_4(tree);//回收空间deleteTree(tree);system("pause");return 0;
}

运行效果：

第一步，随机生成一个二叉树，并逐层打印，然后采用两种序列化方法进行序列化。

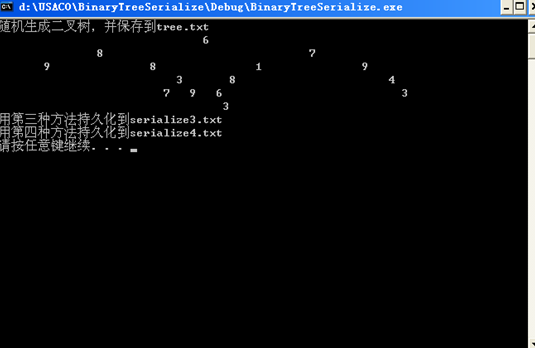
第三种序列化文件为：

[html] view plaincopyprint?

6 1
8 2
9 4
8 5
3 11
7 22
9 23
7 3
1 6
8 12
6 24
3 49
9 7
4 15
3 31

第四种序列化方法为：

[html] view plaincopyprint?

6 8 9 8 3 7 9 7 1 8 6 3 9 4 3 --数据
40e04c7f10000 --位图，用16进制表示

6 8 9 8 3 7 9 7 1 8 6 3 9 4 3       --数据
40e04c7f10000                       --位图，用16进制表示

如上面分析的一样，第四种方法在二叉树是满二叉树或者二叉树的层数比较小的情况下，信息量比较小，但是在树的层比较丰富的情况下，冗余信息非常大。如在15层的二叉树中：

[html] view plaincopyprint?

6 8 9 4 8 3 7 6 4 1 1 6 3 7 9 8 3 7 3 6 3 8 3 7 2 5 6 4 3 1 8 4 2 2 4 3 4 1 9 6 7 4 7 9 5 8 8 7 3 7 9 3 6 3 9 3 3 2 3 5 1 7 5 1 3 9 2 1 3 1 3 3 6 6 2 7 9 4 6 2 7 9 3 2 1 7 4 3 3 1 9 3 1 9 7 6 1 8 8 7 3 2 6 6 8 5 2 3 8 2 5 5 9 4 6 9 2 3 1 2 2 5 2 1 9 9 4 7 6 4 8 5 9 4 8 9 9 9 6 9 5 8 3 9 9 8 3 9 3 5 6 9 6 2 2 6 2 2 5 1 2 1 1 5 6 9 9 5 8 9 5 4 3 8 6 2 3 4 9 9 2 7 7 8 7 6 7 2 2 9 8 1 3 1 3 3 4 3 3 7 3 5 7 9 7 2 4 3 5 2 1 5 3 9 2 8 3 6 3 2 2 1 2 9 3 1 5 5 8 2 4 6 3 4 2 5 5 5 7 6 4 6 5 8 6 2 5 9 6 3 6 3 1 8 1 9 4 6 9 2 4 1 1 5 3 7 2 2 7 1 8 3 4 9 2 6 9 3 8
3e8ffbff1f7901eb3d9867fe6004a7860038b380000606daf48130098068070189048001e8000009022418079e361e000007000838000794808400040800000001f1800018000820008006605401300580650004600000002e82801d8000802120000000018000000002c000118000008000000060000404105800000000400000100000000001928001000800001a21100000000000000008000000020000000000860000000020030000004000000020042000000000000000000000000000000200400098000005000000020000000000000000000000000000000000080000000000000000000000400000000000000000000002000000020180000100000000000000000000000000000000000000000000000000000000000000020000400000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000018000000000000000000000000000000000000000000000060000000000000000000000000000000000000000000000000000000002000600000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000004000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000100000000000000000000000000000000000000

6 8 9 4 8 3 7 6 4 1 1 6 3 7 9 8 3 7 3 6 3 8 3 7 2 5 6 4 3 1 8 4 2 2 4 3 4 1 9 6 7 4 7 9 5 8 8 7 3 7 9 3 6 3 9 3 3 2 3 5 1 7 5 1 3 9 2 1 3 1 3 3 6 6 2 7 9 4 6 2 7 9 3 2 1 7 4 3 3 1 9 3 1 9 7 6 1 8 8 7 3 2 6 6 8 5 2 3 8 2 5 5 9 4 6 9 2 3 1 2 2 5 2 1 9 9 4 7 6 4 8 5 9 4 8 9 9 9 6 9 5 8 3 9 9 8 3 9 3 5 6 9 6 2 2 6 2 2 5 1 2 1 1 5 6 9 9 5 8 9 5 4 3 8 6 2 3 4 9 9 2 7 7 8 7 6 7 2 2 9 8 1 3 1 3 3 4 3 3 7 3 5 7 9 7 2 4 3 5 2 1 5 3 9 2 8 3 6 3 2 2 1 2 9 3 1 5 5 8 2 4 6 3 4 2 5 5 5 7 6 4 6 5 8 6 2 5 9 6 3 6 3 1 8 1 9 4 6 9 2 4 1 1 5 3 7 2 2 7 1 8 3 4 9 2 6 9 3 8 
3e8ffbff1f7901eb3d9867fe6004a7860038b380000606daf48130098068070189048001e8000009022418079e361e000007000838000794808400040800000001f1800018000820008006605401300580650004600000002e82801d8000802120000000018000000002c000118000008000000060000404105800000000400000100000000001928001000800001a21100000000000000008000000020000000000860000000020030000004000000020042000000000000000000000000000000200400098000005000000020000000000000000000000000000000000080000000000000000000000400000000000000000000002000000020180000100000000000000000000000000000000000000000000000000000000000000020000400000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000018000000000000000000000000000000000000000000000060000000000000000000000000000000000000000000000000000000002000600000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000004000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000100000000000000000000000000000000000000

信息量随着层数的增加，信息量成几何级扩大。但是，研究16进制字符串位图数据可以发现里面的数据0出现的特别多，因此下一步可以采用huffman编码等压缩编码方式对字符串数据进行数据压缩。

下一步：采用二进制编码对位图数据进行数据压缩。