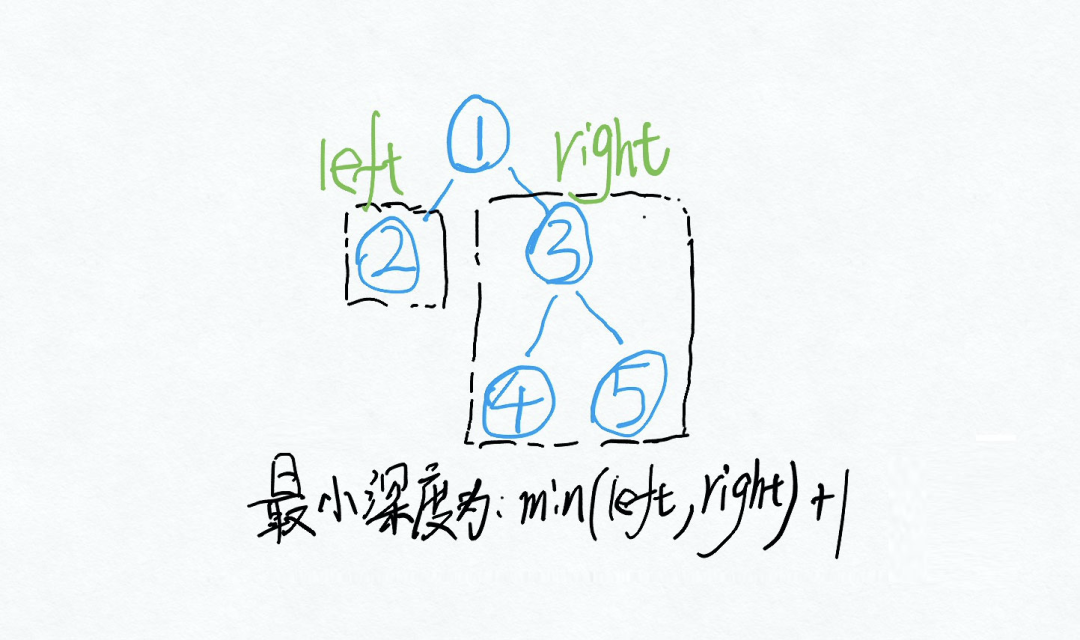
二叉树的最小深度：从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径，最短路径的长度为树的最小深度。

算法一

/** * @description 二叉树最小深度 * @param {*} root 二叉树 */function binaryTreeMinDepth(root) {    // 节点不存在时返回长度为0    if (!root) return 0    // 当节点存在时但是左右子节点不存在，返回长度为1    if (!root.left && !root.right) return 1    // 当左节点不存在，右节点存在，递归求出右节点深度，并加1    if (!root.left) return binaryTreeMinDepth(root.right) + 1    // 当右节点不存在，右节点存在，递归求出左节点深度，并加1    if (!root.right) return binaryTreeMinDepth(root.left) + 1    // 当左右节点都存在时 递归求出左右节点深度，毕竟求出左右节点深度最小值加1    return Math.min(binaryTreeMinDepth(root.right), binaryTreeMinDepth(root.left)) + 1}

算法二

/** * @description 二叉树最小深度 * @param {*} root 二叉树 */function binaryTreeMinDepth(root) {    // 根节点不存在时返回长度为0    if (!root) return 0    // 根节点存在深度为1    let depth = 1    // 声明一个队列默认存放根节点    const queue = [root]    while (queue.length) {        const len  = queue.length        // 遍历栈求出最小深度        for (let i = 0; i < len; i++) {            // 取出栈尾            const current = queue.shift()            // 如果遇到左右节点都不存在直接返回深度            if (!current.left && !current.right) return depth            // 如果左节点存在入栈            if (current.left)  queue.push(current.left)            // 如果右节点存在入栈            if (current.right)  queue.push(current.right)        }        // 深度加1        ++depth    }    // 如果找不到最小深度 则返回-1    return -1}