法线和法线贴图

1、法线无处不在，这是图形学基础中的基础。

2、法线贴图，凹凸图，位移图等等，在图形学历史上有着比较重要的位置，在很多图形学的架构中都有应用，典型的例如延迟渲染架构。

法线

法线，英文名normal。首先，要理解点法线和面法线。

第一个问题：假设一个顶点被N个三角形公用，这个顶点的法线怎么算？

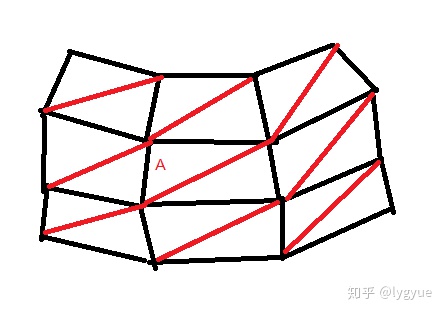
如图，点A的法线应该怎么算才是合理的？

如果是取的面法线，那么多个面公用一个点，取哪个面的才是合理的？

第一个方法：取任意一个面的法线。但是这种做法效果奇差。

第二个方法：计算所有相邻的面的法线，然后取平均值。

这种方案一般情况下，效果还凑合。但是会有其他一些问题。

1、当一个很大的面和一个很小的面邻面，两个面加权求平均，合适吗？

2、并非所有的应用都是需要这种平滑的光照渲染，例如有一些GIS相关的应用，说不定不需要平滑的光照，而是希望得到面与面的清晰边界的光照。

第三个方法：每一个面的法线都要，每个顶点的法线就是面法线。那么，这种情况下，共面的顶点怎么办？当然是多顶点，不适用共享顶点操作模式。例如一个顶点有N个共面，那么这个顶点就不是一个顶点，而是N个顶点，但是坐标是一样的，法线不一样。这种模式，会导致共享顶点减少显存占用的做法失效了。但是，对现代显卡来说，其实顶点数大多数情况下不是很大的开销了，尤其是对于PC来说。

第四个方法：根据相邻面的权重来计算。权重用面积来算。假设有三个面共顶点，三个面的面积分别为A、B、C，法线分别为N1、N2、N3.那么先算A的面积占比p1 = （A / (A + B + C)），法线的占比跟面积的占比一样的。N1 = p1 * (N1 + N2 + N3)。这种做法，效果不怎么样.

我估计，现在图形学上，采用的方案主要是第二跟第三种。我在网上找了两张图，看看第二跟第三种的区别，一眼可以看到。

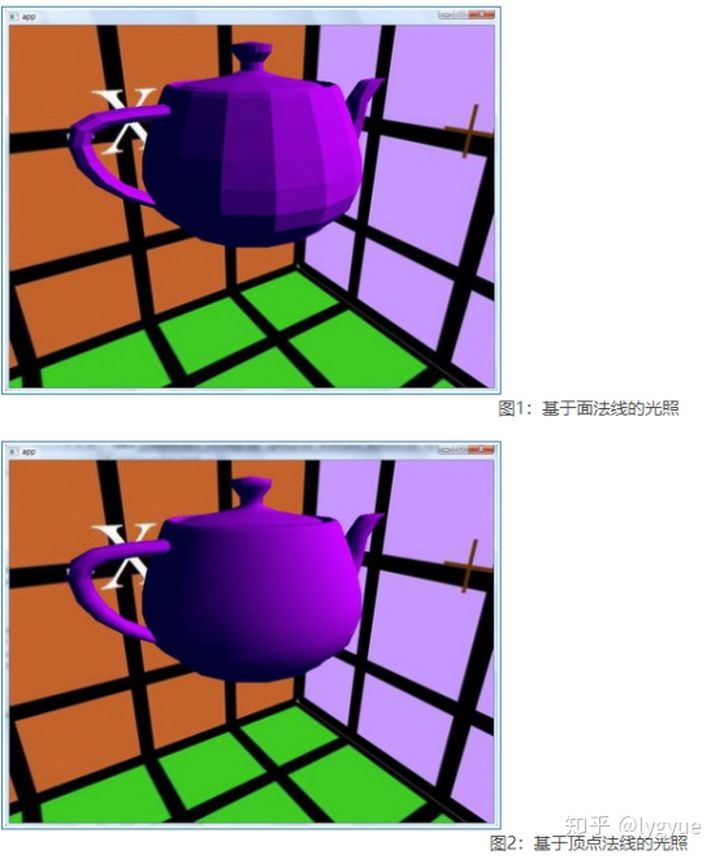
图片来源于网络，侵删。

这么看来，是不是顶点法线才是最合理的？面法线不靠谱？其实不是的，这种完全是看你的需要。看图：

图片来源于网络，侵删。

如果是这种box，你用了顶点法线，出来的就是这种不伦不类的效果了。这种情况下，你大概率需要的是各个面的面法线。所以总结开来，当你需要平滑的时候，用求平均这类顶点法线；当你需要区分的时候，不同面用不同的法线。

法线贴图

为什么需要法线贴图？

图片来源于网络，侵删。

看看这图。如果需要在3D里面渲染这样一个画面，首先是很麻烦，其次是顶点太多。做这样一个模型，估计几万面都是可能的。一些大场景里，满屏的悬崖峭壁，都是这样的效果，面数太多，导致了渲染效率的低下。

那么，能不能做一个面，然后直接上图？当然可以。但是，效果较差，并且实时渲染光照的时候，就更加不理想了。这个时候，就需要用法线贴图了。

法线贴图的意思是：这里还是渲染一个QUAD，两个三角形，但是通过贴图来描述像素的法线。渲染每一个像素的时候，都用的不同的法线，这样，实时光照的时候，能完美模拟出来光照的效果，而且大大降低了计算量。下面，我随手用CPU写一点伪代码，来模拟这个过程，能轻易看出来这个效率的不同。

1、使用模型的渲染方式：假设10000个三角形。

Float4 RenderTriangle(TriangleData)
{Vector3 Pos = CalcPos(); // 一般是线性插值Vector3 Normal = CalcNormal(); // 一般是线性插值Float4 Col = RenderPixel();Return Col;
}Void RenderMesh()
{For(int i = 0; i < 10000; i++){RenderTriangle();}
}

这是直接渲染模型的，线性插值得到法线值。需要迭代N个三角形，效率低。

Float4 RenderTriangle(TriangleData)
{Vector3 Pos = CalcPos(); // 一般是线性插值Vector3 Normal = SampleNormal(); // 采样法线贴图得到法线值Float4 Col = RenderPixel();Return Col;
}Void RenderMesh()
{For(int i = 0; i < 2; i++){RenderTriangle();}
}

这是用法线贴图的。(注意，以上仅仅是简单的CPU模拟，GPU不是这样的。GPU有大量的渲染线程，并且我没记错的话，还是SIMD指令，复杂得多。但是不管怎么样，法线贴图渲染效率的提升都是实打实的。)

那么以上可以看出，法线贴图技术，仅仅是让三角形渲染的时候，多了一个真实的法线值，用于做光照计算，而不能增加顶点值。因为一般时候，顶点值在计算光照的时候都用不到。

那么，是不是所有的复杂模型都可以用法线贴图来解决呢？当然是不可能的。说穿了，法线贴图仅仅是简单的视觉欺骗，一旦凹凸太明显的模型，使用了法线贴图，太靠近的时候，就穿帮了。所以，适用于法线贴图的场合，主要就是凹凸不太明显，细节很多，需要表现实时光照效果，不会太靠近观察的物体。

法线贴图为什么绝大部分都是偏蓝色的？这是一个好问题。彻底理解了这个问题，那么法线的理解基本上可以说登堂入室，脱离了菜鸟行列。

重点1：纹理的像素值，都是0-1之间！没有负数，不能大于1！

这么干有什么好处呢？很简单，一般的浮点数，就是32位，精度有限，还有大量的精度用于描述整数部分，必然导致了小数部分精度的缺失。全部用于描述小数，精度更好。我没有仔细查看过GPU这块用的是哪个浮点数标准，我只隐约记得Nvidia的文档里提过一般浮点数是IEEE754标准，而纹理的就不知道了，但是我相信不会跟一般浮点数一样的，毕竟不需要使用大量的资源来描述整数位了。

所以，法线值储存在贴图里，首先就要normalize，转化为-1到1之间。然后再因为不能有负数，需要再转换到0-1之间，一般有大概这样的函数：

Float3 DecodeNormal(float3 n)
{Return(n * 2 - 1.0f);
}Float3 EncodeNormal(float3 n)
{Return(n + 1.0f) * 0.5;
}

据说这个函数有人玩出花来的，例如什么压缩到16位贴图减少显存占用，这个其实比较简单，因为normalize之后的法线值，其实是x ^2 + y^2 + z^2 = 1;那么你保存了x跟y岂不是可以反过来算出z了嘛。但是这种做法虽然降低了显存占用，同时也降低了效率啊，需要开方一次。其他据说还有一大堆乱七八糟的优化，我只是耳闻，反正我没有干过。有兴趣的也可以自己试试看。

重点 2：模型有本地坐标系，世界坐标系。渲染的时候，必须变换到世界坐标系才能正确渲染。这个变换一般都很简单，就是一行代码：

Float4 WorldPos = WorldMatrix * LocalPos;

那么问题来了，法线怎么弄呢？当你没有用到法线贴图的时候，其实也是一样的：

Float4 WorldNormal = WorldMatrix * LocalNormal;

那么，你使用了法线贴图呢？

我们需要这么干：

Float4 Normal = tex2D(NormalTexture, UV);

Float4 RealNormal = DecodeNormal(Normal); // 0,1转换到-1，1

Float4 WorldNormal = WorldMatrix * RealNormal;

Float4 Col = CalcLighting(WorldNormal, Light);// 法线和光照计算颜色。

上面代码有什么问题吗？其实，如果就一般的程序来说，一点问题都没有。甚至更糟糕的垃圾代码，都没有问题。我见过无数比这糟糕得到的代码，照样跑得666.

图形学为什么相对比较难？因为图形学对性能有极致的需求。以上代码，对性能上有一定的损耗。主要表现在哪里？

首先，这里的UV是需要三角形插值得到的，这就导致了这部分代码必须只能运行在PS（像素着色器）上。也就是说，每个像素都需要执行一遍。

其实这也不是什么大问题。但是，有更好的优化方式啊。我可以把Light的坐标，转换到法线贴图的本地坐标系，然后进行光照，结果是一样的啊，只要在同一个坐标系即可。而Light的坐标转换，只需要在VS里面算一次即可，不需要在PS里面反复算。

所以，你们看到法线贴图相关的shader，大概率都是这样的：

Void VS()

{

float3 binormal = cross(tangent.xyz, normal); // tangent是切线，需要外部传入

float3x3 rotation = float3x3(tangent.xyz, binormal, normal);

oTSLightDir = mul(rotation, lightDir); // lightDir是光照方向

}

Float4 PS()

{

float3 lightVec = normalize(TSlightDir).xyz;

float3 Normal= DecodeNormal(tex2D(normalMap, uv).xyz);

Return CalcLighting(Normal, lightVec );

}

看到了吗，这个算法比上面的算法，效率上是要更高的。高多少？天知道，跟很多因素有关。法线贴图少的时候，这个提升其实可以忽略不计，但是肯定是提升。

以上这个坐标系，叫做切线坐标系。首先，任意一个三角形，先计算一个Normal，然后再计算一个切线。根据法线跟切线的两两垂直关系，叉乘（crossProduct），得到副法线，构建坐标系。三角形的法线好计算，已知三个顶点，根据面的方向，两两叉乘可以得到法线，这点代码到处都能找到。那么切线是怎么算的呢？我没记错的话，我记得是用偏微分方程，以U坐标方向为切线方向来算的，那么V方向就是副法线方向（这部分不保证绝对正确，懒得去查资料了，大概理解一下原理即可，想知道的自己去查一下）。

除了效率原因，还有另外一个原因，据说是形变。假设是模型，使用了形变，如果法线贴图储存的是本地坐标系，这个世界变换并不能体现这个形变，而且法线贴图的计算一般都是再MAX，玛雅之类的软件里，引擎一般不提供，修改法线贴图就很麻烦了。而使用了切线坐标系，是可以实现形变的。形变之后，重新计算Normal跟Tangent即可。但是，这其实也是挺麻烦的事，一般来说，使用到法线贴图的模型，都是一些大平面的细节模型，形变这个因素我没碰到过。

回到主题，为什么法线贴图是偏蓝色？很明显了，在切线坐标系里，定义顺序是Tangent、Binormal、Normal，也就是说，Normal处于z这个方向。而对于一个三角形而言，绝大多数时候，法线值都是垂直于这个面的。显而易见，法线贴图的法线值大多数时候是接近于（0，0，1）的，当然是接近于蓝色了。

当然了，这不是绝对的，跟引擎有关，也跟自己的处理有关。例如压缩到16位的法线贴图，例如只保存x，y的，不就是偏黑色了嘛？没搞过，按道理是这样的