第一种:用2整除的方式。
用2整除十进制整数,得到一个商和余数;再用2去除商,又会得到一个商和余数,如此重复,直到商为小于1时为止,然后把先得到余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,以此排列起来。
注1:当一个整数除另一个整数得到整数商而没有余数时,叫做整除。如2除6得3,就说2能整除6或6能被2整除。
注2:除以是被除数在前,除数在后;除是除数在前,被除数在后。如32÷8=4可描述为:8除32等于4,或者32除以8等于4。
以十进制100转换为二进制为例:
100/2=50余0;50/2=25余0;25/2=12余1;12/2=6余0;6/2=3余0;3/2=1余1。以此排列十进制的100转换成二进制是:1100100。
计算如下:
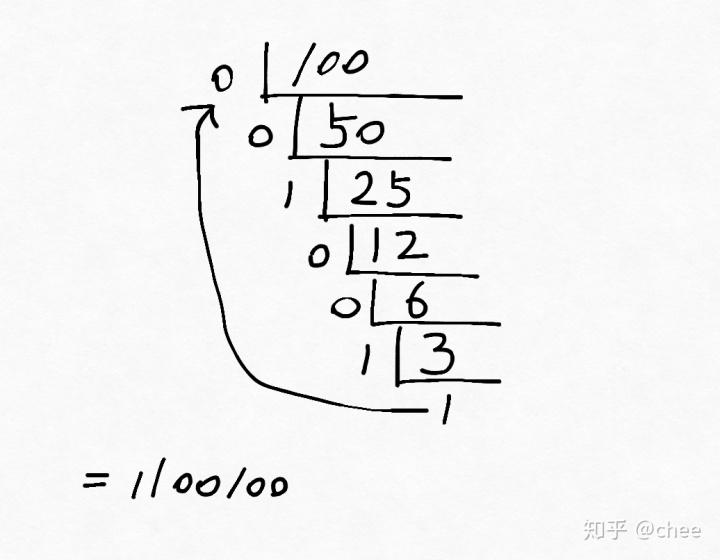
第二种:1248比表法(学名不知道,自己取的)。
对比表如下:
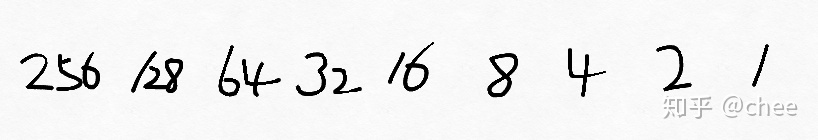
以十进制100转换为二进制为例:
从左至右依次开始:100比128小,取0;100比64大,取1,剩36;36比32大,取1,剩4;4比16小,取0;4比8小,取0;4不比4小,取1,剩0;0比2小,取0;0比1小,取0。最终得:01100100。
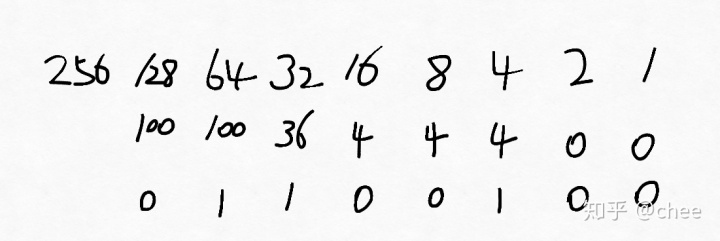
得:1100100
又如十进制168转换为二进制:
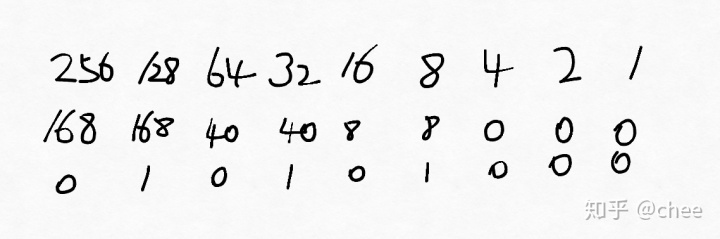
得:10101000



 号用法...)







...)




上运行python总结)
学习笔记)

