性能度量RMSE

回归问题的典型性能度量是均方根误差（RMSE:Root Mean Square Error）。如下公式。

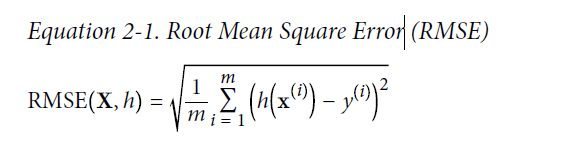
1. m为是你计算RMSE的数据集中instance的数量。
2. x⁽ⁱ⁾是第i个实例的特征值向量 ,y⁽ⁱ⁾是其label（期望的模型输出）。如下：
   
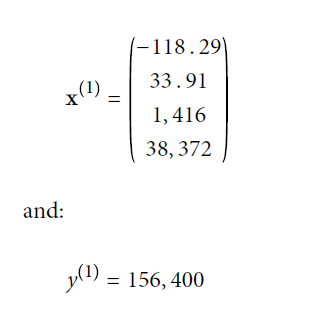
3. X是包含了所有实例的特征值（不包含label）的矩阵。每行代表一个实例，并且每行等于x⁽ⁱ⁾向量的转置：(x⁽ⁱ⁾)^T 。 下图矩阵中的第一行为2中向量的转置（列向量变为行向量）。
   
   
   
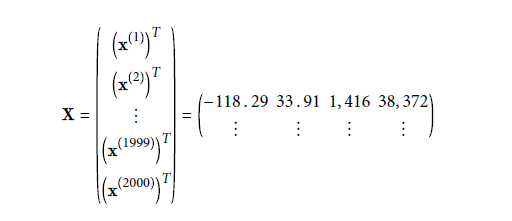
4. h是预测函数，当输入是某实例的特征向量x⁽ⁱ⁾ ，应用函数之后，结果为ŷ⁽ⁱ⁾=h(x⁽ⁱ⁾). ŷ也叫作y-hat. 比如：对第一个实例应用函数h后结果为158400，即ŷ⁽¹⁾=h(x⁽¹⁾)=158400。那么预测误差/错误为ŷ⁽¹⁾-y⁽¹⁾ = 158400 - 156400 = 2000.
5. RMSE(X,h) 是在数据集X上应用于函数h计算的cost function。 

以上，我们使用小写斜体表示标量(m,y⁽ⁱ⁾)，函数名(h)。小写粗体表示向量(x⁽ⁱ⁾). 大写粗体表示矩阵(X).

还有一种度量方法为： Mean Absolute Error. 理解起来也比较简单。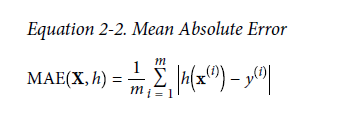

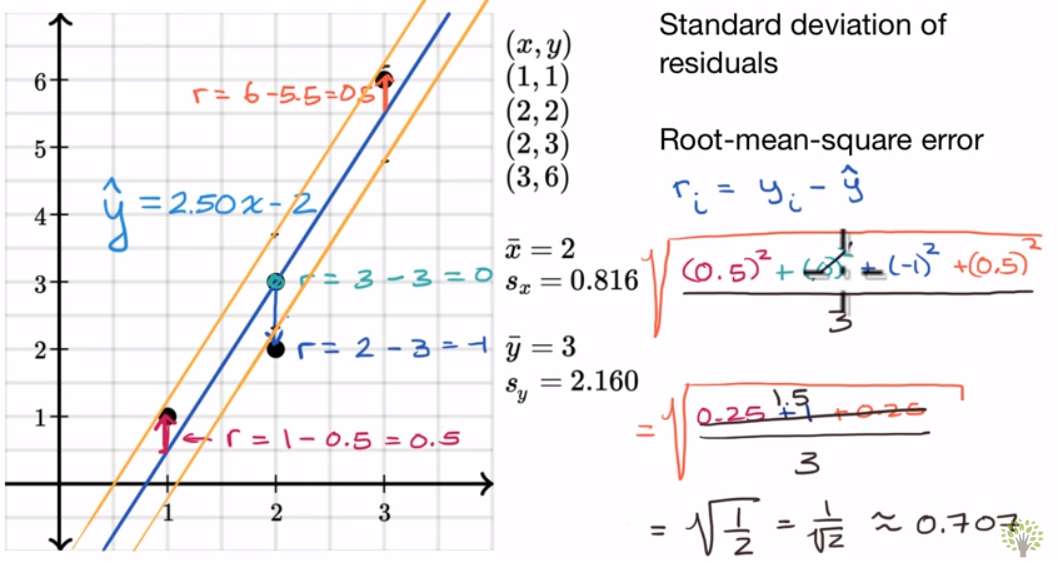
下面是一张图，通过线性关系生动解释了RMSE。4个黑色的点是数据集（包括标签），蓝色的线是我们的预测函数h: ŷ=2.50x-2。从而可以求出RMSE为0.707.与之前不同的是这里取m为3(m-1)而不是4。

结论： RMSE越小，说明模型越fit数据。