#题目：有 n 个整数，使其前面各数顺序向后移 m 个位置，最后 m 个数变成最前面的 m 个数
#!/usr/bin/python

-- coding: UTF-8 --

if name == ‘main’:
n = int(input(‘整数 n 为:\n’))
m = int(input(‘向后移 m 个位置为:\n’))

def move(array,n,m):array_end = array[n - 1]for i in range(n - 1,-1,- 1):array[i] = array[i - 1]array[0] = array_endm -= 1if m > 0:move(array,n,m)number = []
for i in range(n):number.append(int(input('输入一个数字:\n')))
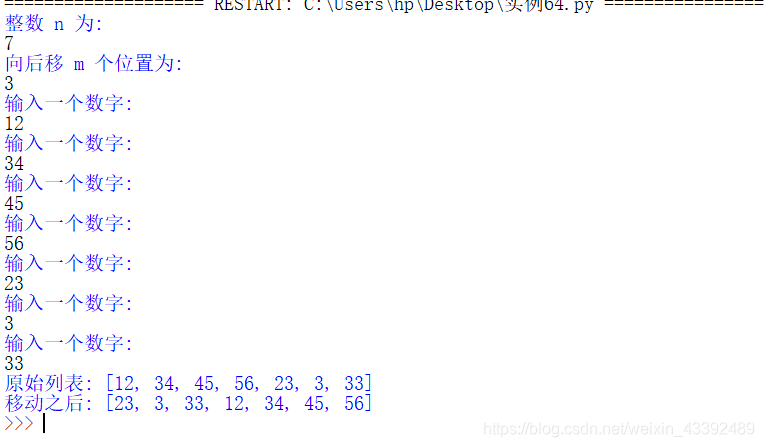
print ('原始列表:',number)move(number,n,m)print ('移动之后:',number)