【问题描述】[中等]

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示：2 <= n <= 58

【解答思路】

1. 贪心思想&数学证明

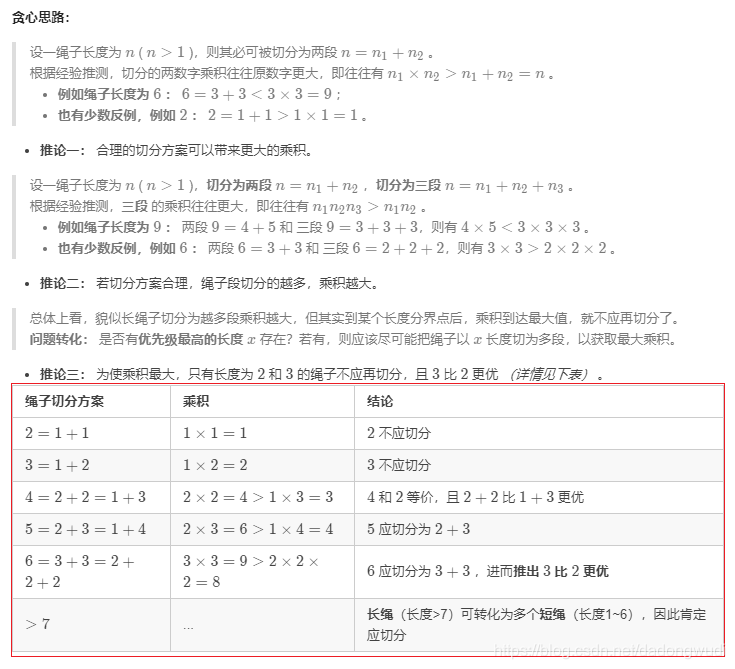
时间复杂度：O(1) 空间复杂度：O(1)

class Solution {public int cuttingRope(int n) {if(n <= 3) return n - 1;int a = n / 3, b = n % 3;if(b == 0) return (int)Math.pow(3, a);if(b == 1) return (int)Math.pow(3, a - 1) * 4;return (int)Math.pow(3, a) * 2;}
}

快速幂 + 求余

public int cuttingRope(int n) {if(n <= 3) return n - 1;int b = n % 3, p = 1000000007;long rem = 1,x=3;for(int a = n/3-1 ;a>0; a/=2){if(a%2 ==1){rem = (rem*x)%p;}x = (x*x)%p;}if(b == 0){return (int)(rem*3%p);}if(b == 1){return (int)(rem*4%p);}//b =2 return (int)(rem*6%p);}

2. 背包动态规划

第一层循环枚举物品，第二层循环枚举背包体积
时间复杂度：O(N) 空间复杂度：O(N)

 public int cuttingRope(int n) {int[] dp = new int[n+1];dp[0] = 1;for (int i = 1; i <= (n+1)/2; i++) {for (int j = i; j <= n; j++) {dp[j] = Math.max(dp[j], dp[j-i] * i);}}return dp[n];}

3. 动态规划

考虑最后一步的情况，即最后剪的一下，会把绳子分为两部分，且两部分的结果互不影响

定义 dp[i] 表示长度i的绳子能得到的最大乘积

则 dp[i] 等于 在绳子区间[0, i)之间剪开的两部分乘积最大值

如果剪开位置为k，则区间分为[0, k)和[k, i)两部分

第一部分长度为k, 第二部分长度为i-k

第二部分存在剪和不剪两种情况，剪的时候值为dp[i-k]，不剪的时候取（i-k)

于是得到状态转换方程：

dp[i] = max{ k * dp[i-k], k * (i-k)} (2<=k<=i)

时间复杂度：O(N) 空间复杂度：O(N)

 public int cuttingRope(int n) {int[] dp = new int[n+1];dp[1] = 1;dp[2] = 1;for (int i = 3; i<=n; i++){for (int k = 2; k <= i-1; k++){dp[i] = Math.max(dp[i], Math.max(k*(i-k), k*dp[i-k]));}}return dp[n];}

【总结】

1.数学高数求导 求最大最小值神器

2.动态规划流程

第 1 步：设计状态
第 2 步：状态转移方程
第 3 步：考虑初始化
第 4 步：考虑输出
第 5 步：考虑是否可以状态压缩

3. 不要想当然，要有数学证明，思路错，代码怎么调都是做无用功

4.快速幂

public long remainder(long x, int a, int p){long rem = 1;while( a > 0){if(a%2 ==1){rem = (rem*x)%p;}x = (x*x)%p;a /=2;}return  rem;}

转载链接：https://leetcode-cn.com/problems/jian-sheng-zi-lcof/solution/mian-shi-ti-14-i-jian-sheng-zi-tan-xin-si-xiang-by/
参考链接：https://leetcode-cn.com/problems/jian-sheng-zi-lcof/solution/xu-lie-xing-dong-tai-gui-hua-by-muyids-2/